1,001 Calculus Practice Problems
Part I
The Questions
Chapter 12
Inverse Trigonometric Functions, Hyperbolic Functions, and L'Hôpital's Rule
This chapter looks at the very important inverse trigonometric functions and the hyperbolic functions. For these functions, you see lots of examples related to finding derivatives and integration as well. Although you don't spend much time on the hyperbolic functions in most calculus courses, the inverse trigonometric functions come up again and again; the inverse tangent function is especially important when you tackle the partial fraction problems of Chapter 14. At the end of this chapter, you experience a blast from the past: limit problems!
The Problems You'll Work On
This chapter has a variety of limit, derivative, and integration problems. Here's what you work on:
· Finding derivatives and antiderivatives using inverse trigonometric functions
· Finding derivatives and antiderivatives using hyperbolic functions
· Using L'Hôpital's rule to evaluate limits
What to Watch Out For
Here are a few things to consider for the problems in this chapter:
· The derivative questions just involve new formulas; the power, product, quotient, and chain rules still apply.
· Know the definitions of the hyperbolic functions so that if you forget any formulas, you can easily derive them. They're simply defined in terms of the exponential function, ex.
· Although L'Hôpital's rule is great for many limit problems, make sure you have an indeterminate form before you use it, or you can get some very incorrect solutions.
Finding Derivatives Involving Inverse Trigonometric Functions
750–762 Find the derivative of the given function.
750. ![]()
751. ![]()
752. ![]()
753. ![]()
754. ![]()
755. ![]()
Note: The derivative formula for sec−1 t varies, depending on the definition used. For this problem, use the formula 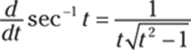
756. y = csc−1 e2x
757. ![]()
Note: The derivative formula for sec−1 x varies, depending on the definition used. For this problem, use the formula 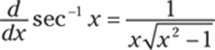 .
.
758. ![]()
759. ![]()
760. ![]()
761. ![]()
762. ![]()
Finding Antiderivatives by Using Inverse Trigonometric Functions
763–774 Find the indefinite integral or evaluate the definite integral.
763. ![]()
764. 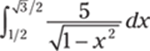
765. 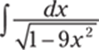
766. 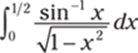
767. ![]()
768. 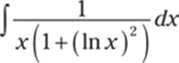
769. 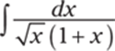
770. 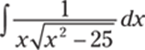
771. 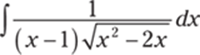
772. 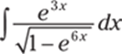
773. ![]()
774. 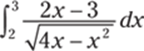
Evaluating Hyperbolic Functions Using Their Definitions
775–779 Use the definition of the hyperbolic functions to find the values.
775. sinh 0
776. cosh (ln 2)
777. coth (ln 6)
778. tanh 1
779. ![]()
Finding Derivatives of Hyperbolic Functions
780–789 Find the derivative of the given function.
780. y = cosh2 x
781. ![]()
782. ![]()
783. ![]()
784. y = tanh(sinh x)
785. ![]()
786. ![]()
787. ![]()
788. ![]()
789. 
Finding Antiderivatives of Hyperbolic Functions
790–799 Find the antiderivative.
790. ![]()
791. ![]()
792. ![]()
793. ![]()
794. ![]()
795. ![]()
796. 
797. 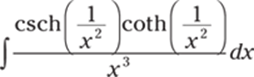
798. ![]()
799. 
Evaluating Indeterminate Forms Using L'Hôpital's Rule
800–831 If the limit is an indeterminate form, evaluate the limit using L'Hôpital's rule. Otherwise, find the limit using any other method.
800. ![]()
801. ![]()
802. ![]()
803. 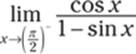
804. ![]()
805. ![]()
806. 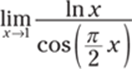
807. ![]()
808. 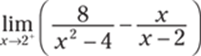
809. 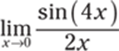
810. ![]()
811. ![]()
812. ![]()
813. 
814. 
815. ![]()
816. ![]()
817. ![]()
818. ![]()
819. ![]()
820. ![]()
821. ![]()
822. ![]()
823. ![]()
824. 
825. ![]()
826. ![]()
827. ![]()
828. ![]()
829. ![]()
830. 
831. ![]()