1,001 Calculus Practice Problems
Part I
The Questions
Chapter 13
U-Substitution and Integration by Parts
In this chapter, you encounter some of the more advanced integration techniques: u-substitution and integration by parts. You use u-substitution very, very often in integration problems. For many integration problems, consider starting with a u-substitution if you don't immediately know the antiderivative. Another common technique is integration by parts, which comes from the product rule for derivatives. One of the difficult things about these problems is that even when you know which procedure to use, you still have some freedom in how to proceed; what to do isn't always clear, so dive in and try different things.
The Problems You'll Work On
This chapter is the start of more challenging integration problems. You work on the following skills:
· Using u-substitution to find definite and indefinite integrals
· Using integration by parts to find definite and indefinite integrals
What to Watch Out For
Here are a few things to keep in mind while working on the problems in this chapter:
· Even if you know you should use a substitution, there may be different substitutions to try. As a rule, start simple and make your substitution more complex if your first choice doesn't work.
· When using a u-substitution, don't forget to calculate du, the differential.
· You can algebraically manipulate both du and the original u-substitution, so play with both!
· For the integration by parts problems, if your pick of u and dv don't seem to be working, try switching them.
Using u-Substitutions
832–857 Use substitution to evaluate the integral.
832. ![]()
833. ![]()
834. ![]()
835. 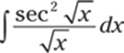
836. 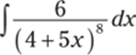
837. ![]()
838. ![]()
839. 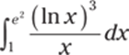
840. ![]()
841. ![]()
842. ![]()
843. ![]()
844. ![]()
845. ![]()
846. 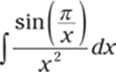
847. 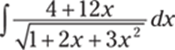
848. ![]()
849. ![]()
850. ![]()
851. 
852. ![]()
853. ![]()
854. ![]()
855. ![]()
856. ![]()
857. ![]()
Using Integration by Parts
858–883 Use integration by parts to evaluate the integral.
858. ![]()
859. ![]()
860. ![]()
861. ![]()
862. ![]()
863. ![]()
864. ![]()
865. ![]()
866. ![]()
867. ![]()
868. ![]()
869. ![]()
870. ![]()
871. ![]()
872. ![]()
873. ![]()
874. ![]()
875. ![]()
876. ![]()
877. ![]() , where m ≠ 0
, where m ≠ 0
878. ![]()
879. ![]()
880. ![]()
881. ![]()
882. ![]()
883. ![]()