1,001 Calculus Practice Problems
Part I
The Questions
Chapter 15
Improper Integrals and More Approximating Techniques
The problems in this chapter involve improper integrals and two techniques to approximate definite integrals: Simpson's rule and the trapezoid rule. Improper integrals are definite integrals with limits thrown in, so those problems require you to make use of many different calculus techniques; they can be quite challenging. The last few problems of the chapter involve using Simpson's rule and the trapezoid rule to approximate definite integrals. When you know the formulas for these approximating techniques, the problems are more of an arithmetic chore than anything else.
The Problems You'll Work On
This chapter involves the following tasks:
· Solving improper integrals using definite integrals and limits
· Using comparison to show whether an improper integral converges or diverges
· Approximating definite integrals using Simpson's rule and the trapezoid rule
What to Watch Out For
Here are a few pointers to help you finish the problems in this chapter:
· Improper integrals involve it all: limits, l'Hôpital's rule, and any of the integration techniques.
· The formulas for Simpson's rule and the trapezoid rule are similar, so don't mix them up!
· If you're careful with the arithmetic on Simpson's rule and the trapezoid rule, you should be in good shape.
Convergent and Divergent Improper Integrals
964–987 Determine whether the integral is convergent or divergent. If the integral is convergent, give the value.
964. 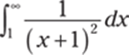
965. ![]()
966. ![]()
967. ![]()
968. ![]()
969. ![]()
970. ![]()
971. ![]()
972. ![]()
973. 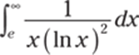
974. ![]()
975. ![]()
976. ![]()
977. ![]()
978. ![]()
979. ![]()
980. ![]()
981. ![]()
982. ![]()
983. ![]()
984. ![]()
985. 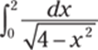
986. ![]()
987. ![]()
The Comparison Test for Integrals
988–993 Determine whether the improper integral converges or diverges using the comparison theorem for integrals.
988. ![]()
989. ![]()
990. 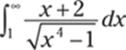
991. ![]()
992. 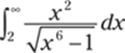
993. ![]()
The Trapezoid Rule
994–997 Use the trapezoid rule with the specified value of n to approximate the integral. Round to the nearest thousandth.
994. ![]() with n = 6
with n = 6
995. ![]() with n = 4
with n = 4
996. ![]() with n = 8
with n = 8
997. ![]() with n = 4
with n = 4
Simpson's Rule
998–1,001 Use Simpson's rule with the specified value of n to approximate the integral. Round to the nearest thousandth.
998. ![]() with n = 6
with n = 6
999. ![]() with n = 4
with n = 4
1000. ![]() with n = 8
with n = 8
1001. ![]() with n = 4
with n = 4