1,001 Calculus Practice Problems
Part I
The Questions
Chapter 2
Trigonometry Review
In addition to having a strong algebra background, you need a strong trigonometry skill set for calculus. You want to know the graphs of the trigonometric functions and to be able to evaluate trigonometric functions quickly. Many calculus problems require one or more trigonometric identities, so make sure you have more than a few of them memorized or at least can derive them quickly.
The Problems You'll Work On
In this chapter, you solve a variety of fundamental trigonometric problems that cover topics such as the following:
· Understanding the trigonometric functions in relation to right triangles
· Finding degree and radian measure
· Finding angles on the unit circle
· Proving identities
· Finding the amplitude, period, and phase shift of a periodic function
· Working with inverse trigonometric functions
· Solving trigonometric equations with and without using inverses
What to Watch Out For
Remember the following when working on the trigonometry review questions:
· Being able to evaluate the trigonometric functions at common angles is very important since they appear often in problems. Having them memorized will be extremely useful!
· Watch out when solving equations using inverse trigonometric functions. Calculators give only a single solution to the equation, but the equation may have many more (sometimes infinitely many solutions), depending on the given interval. Thinking about solutions on the unit circle is often a good way to visualize the other solutions.
· Although you may be most familiar with using degrees to measure angles, radians are used almost exclusively in calculus, so learn to love radian measure.
· Memorizing many trigonometric identities is a good idea because they appear often in calculus problems.
Basic Trigonometry
103–104 Evaluate ![]() ,
, ![]() , and
, and ![]() for the given right triangle. Remember to rationalize denominators that contain radicals.
for the given right triangle. Remember to rationalize denominators that contain radicals.
103. 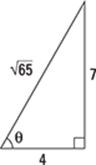
104. 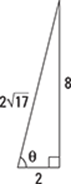
105–108 Evaluate the trig function. Remember to rationalize denominators that contain radicals.
105. Given ![]() , where
, where ![]() , find
, find ![]() .
.
106. Given ![]() , where
, where ![]() , find
, find ![]() .
.
107. Given ![]() , where
, where ![]() and
and ![]() , find
, find ![]() .
.
108. Given ![]() , where
, where ![]() , find
, find ![]() .
.
Converting Degree Measure to Radian Measure
109–112 Convert the given degree measure to radian measure.
109. 135 °
110. –280°
111. 36 °
112. –315°
Converting Radian Measure to Degree Measure
113–116 Convert the given radian measure to degree measure.
113. ![]() rad
rad
114. ![]() rad
rad
115. ![]() rad
rad
116. ![]() rad
rad
Finding Angles in the Coordinate Plane
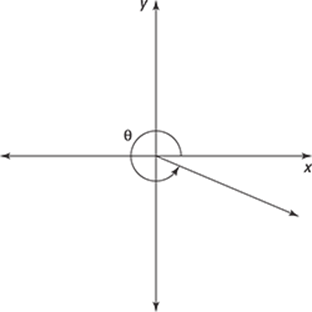
117–119 Choose the angle that most closely resembles the angle in the given diagram.
117. Using the diagram, find the angle measure that most closely resembles the angle ![]() .
.
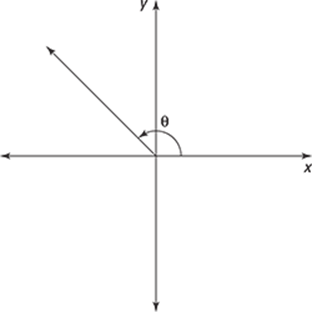
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
118. Using the diagram, find the angle measure that most closely resembles the angle ![]() .
.
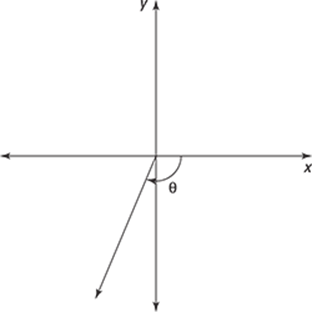
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
119. Using the diagram, find the angle measure that most closely resembles the angle ![]() .
.
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Finding Common Trigonometric Values
120–124 Find ![]() ,
, ![]() , and
, and ![]() for the given angle measure. Remember to rationalize denominators that contain radicals.
for the given angle measure. Remember to rationalize denominators that contain radicals.
120. ![]()
121. ![]()
122. ![]()
123. ![]()
124. ![]()
Simplifying Trigonometric Expressions
125–132 Determine which expression is equivalent to the given one.
125. ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
126. sec x – cos x
(A) 1
(B) sin x
(C) tan x
(D) cos x cot x
(E) sin x tan x
127. (sin x + cos x)2
(A) 2 + sin 2x
(B) 2 + cos 2x
(C) 1 + sec 2x
(D) 1 + sin 2x
(E) 1 + cos 2x
128. sin(π – x)
(A) cos x
(B) sin x
(C) csc x
(D) sec x
(E) tan x
129. sin x sin 2x + cos x cos 2x
(A) cos x
(B) sin x
(C) csc x
(D) sec x
(E) tan x
130. ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
131. ![]()
(A) csc x + cot x
(B) sec x + cot x
(C) csc x – cot x
(D) sec x – tan x
(E) csc x – tan x
132. ![]()
(A) 5 cos3θ – 3 cos θ
(B) 2 cos3θ – 3 cos θ
(C) 4 cos3θ – 3 cos θ
(D) 4 cos3θ + 3 cos θ
(E) 2 cos3θ + 5 cos θ
Solving Trigonometric Equations
133–144 Solve the given trigonometric equations. Find all solutions in the interval [0, 2π].
133. 2 sin x – 1 = 0
134. sin x = tan x
135. 2 cos2 x + cos x – 1 = 0
136. ![]()
137. 2 sin2 x – 5 sin x – 3 = 0
138. cos x = cot x
139. ![]()
140. sin 2x = cos x
141. 2 cos x + sin 2x = 0
142. 2 + cos 2x = –3 cos x
143. tan(3x) = –1
144. cos(2x) = cot(2x)
Amplitude, Period, Phase Shift, and Midline
145–148 Determine the amplitude, the period, the phase shift, and the midline of the function.
145. ![]()
146. ![]()
147. f (x) = 2 – 3 cos(πx – 6)
148. ![]()
Equations of Periodic Functions
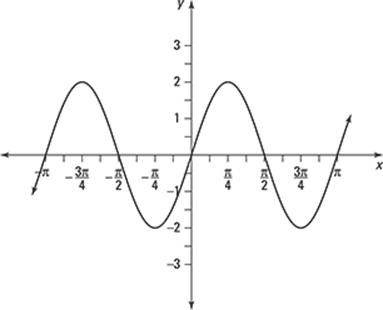
149–154 Choose the equation that describes the given periodic function.
149. 
(A) f (x) = 2 sin(2x)
(B) f (x) = –2 sin(2x)
(C) f (x) = 2 sin(x)
(D) f (x) = 2 sin(πx)
(E) ![]()
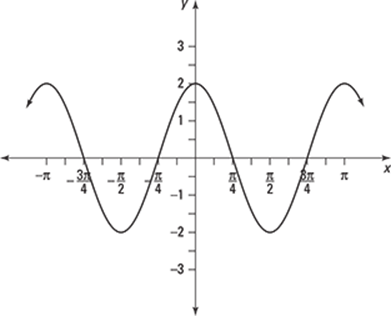
150. 
(A) f (x) = 2 cos(x)
(B) f (x) = 2 cos(2x)
(C) f (x) = 2 cos(πx)
(D) f (x) = –2 cos(2x)
(E) ![]()
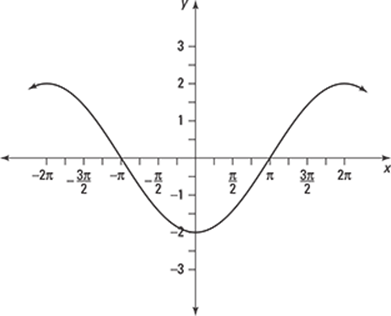
151. 
(A) f (x) = 2 cos(2x) + 1
(B) f (x) = –2 cos(2x) + 2
(C) f (x) = 2 cos(2x)
(D) ![]()
(E) f (x) = 2 cos(πx)
152. 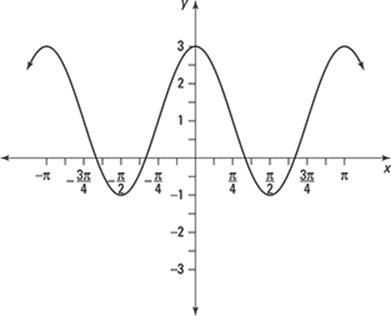
(A) f (x) = –2 cos(2x)
(B) f (x) = –2 cos(2x) + 2
(C) f (x) = 2 cos(2x) + 1
(D) f (x) = 2 cos(πx) + 1
(E) ![]()
153. 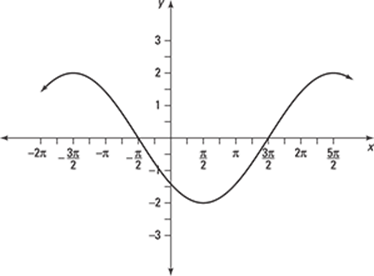
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
154. 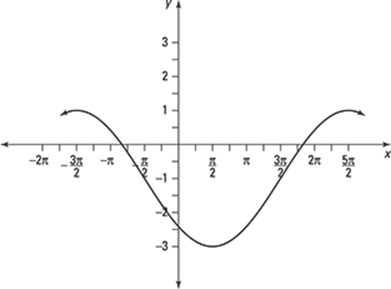
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Inverse Trigonometric Function Basics
155–160 Evaluate the inverse trigonometric function for the given value.
155. Find the value of 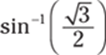 .
.
156. Find the value of arctan(–1).
157. Find the value of 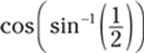 .
.
158. Find the value of 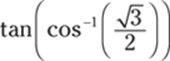 .
.
159. Find the value of ![]() .
.
160. Find the value of ![]() .
.
Solving Trigonometric Equations Using Inverses
161–166 Solve the given trigonometric equation using inverses. Find all solutions in the interval [0, 2π].
161. sin x = 0.4
162. cos x = –0.78
163. 5 sin(2x) + 1 = 4
164. 7 cos(3x) – 1 = 3
165. 2 sin2 x + 8 sin x + 5 = 0
166. 3 sec2 x + 4 tan x = 2