1,001 Calculus Practice Problems

Part I

The Questions

Chapter 4

The derivative is one of the great ideas in calculus. In this chapter, you see the formal definition of a derivative. Understanding the formal definition is crucial, because it tells you what a derivative actually is. Unfortunately, computing the derivative using the definition can be quite cumbersome and is often very difficult. After finding derivatives using the definition, you see problems that use the power rule, which is the start of some techniques that make finding the derivative much easier — although still challenging in many cases.

The Problems You'll Work On

In this chapter, you see the definition of a derivative and one of the first shortcut formulas, the power rule. Here's what the problems cover:

· Using a variety of algebraic techniques to find the derivative using the definition of a derivative

· Evaluating the derivative at a point using a graph and slopes of tangent lines

· Encountering a variety of derivative questions that you can solve using the power rule

What to Watch Out For

Using the definition of a derivative to evaluate derivatives can involve quite a bit of algebra, so be prepared. Having all the shortcut techniques is very nice, but you'll be asked to find derivatives for complicated functions, so the problems will still be challenging! Keep some of the following points in mind:

· Remember your algebra techniques: factoring, multiplying by conjugates, working with fractions, and more. Many students get tripped up on one part and then can't finish the problem, so know that many problems require multiple steps.

· When interpreting the value of a derivative from a graph, think about the slope of the tangent line on the graph at a given point; you'll be well on your way to finding the correct solution.

· Simplifying functions using algebra and trigonometric identities before finding the derivative makes many problems much easier. Simplifying is one of the very first things you should consider when encountering a “find the derivative” question of any type.

Determining Differentiability from a Graph

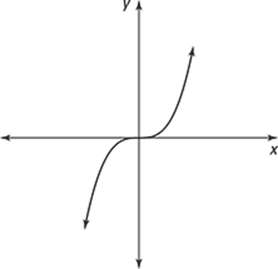
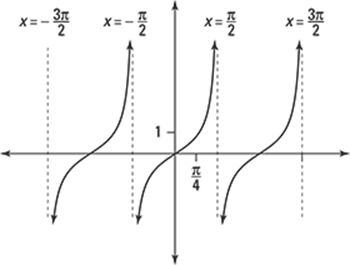
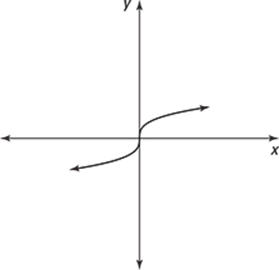
272–276 Use the graph to determine for which values of x the function is not differentiable.

272.

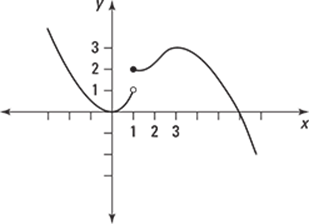
273.

274.

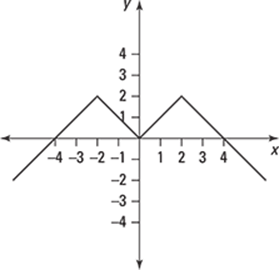
275.

276.

Finding the Derivative by Using the Definition

277–290 Find the derivative by using the definition .

277. f (x) = 2x – 1

278. f (x) = x²

279. f (x) = 2 + x

280.

281. f (x) = x³ – x²

282. f (x) = 3x² + 4x

283.

284.

285.

286. f (x) = x³ + 3x

287.

288.

289.

290.

Finding the Value of the Derivative Using a Graph

291–296 Use the graph to determine the solution.

291.

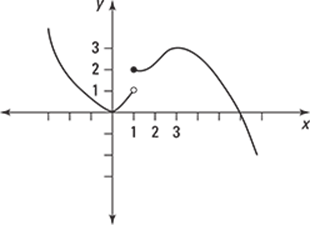
Estimate the value of f'(3) using the graph.

292.

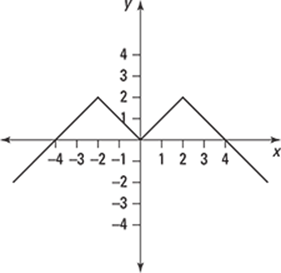
Estimate the value of f'(–1) using the graph.

293.

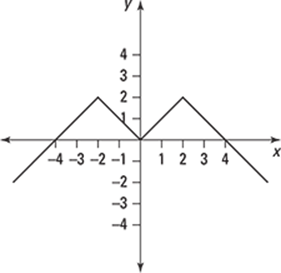
Estimate the value of f'(–3) using the graph.

294.

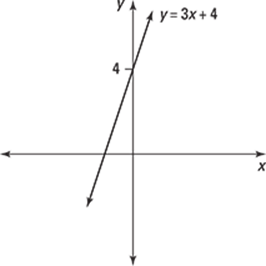
Based on the graph of y = 3x + 4, what does f'(–22π³) equal?

295.

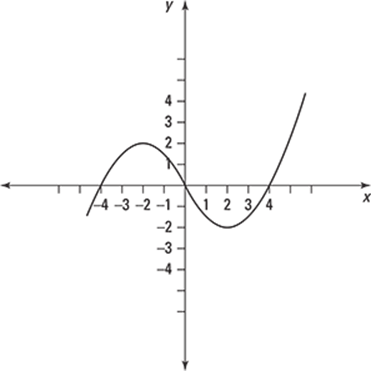
Based on the graph, arrange the following from smallest to largest: f'(–3), f'(–2), and f'(1).

296.

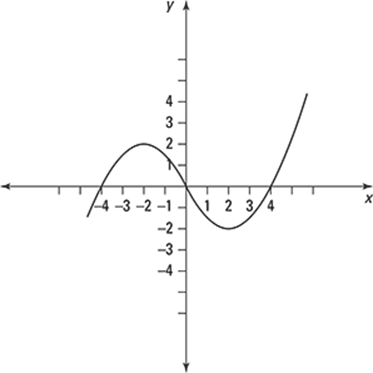
Based on the graph, arrange the following from smallest to largest: f'(1), f'(2), f'(5), and 0.1.

Using the Power Rule to Find Derivatives

297–309 Use the power rule to find the derivative of the given function.

297. f (x) = 5x + 4

298. f (x) = x² + 3x + 6

299. f (x) = (x + 4)(2x – 1)

300. f (x) = π³

301.

302.

303.

304.

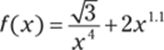
305.

306.

307. f (x) = (x⁻³ + 4)(x⁻² – 5x)

308. f (x) = 4x⁴ – x² + 8x + π²

309.

Finding All Points on a Graph Where Tangent Lines Have a Given Value

310–311 Find all points on the given function where the slope of the tangent line equals the indicated value.

310. Find all x values where the function f (x) = x³ – x² – x + 1 has a horizontal tangent line.

311. Find all x values where the function f (x) = 6x³ + 5x – 2 has a tangent line with a slope equal to 6.