1,001 Calculus Practice Problems
Part I
The Questions
Chapter 7
Implicit Differentiation
When you know the techniques of implicit differentiation (this chapter) and logarithmic differentiation (covered in Chapter 6), you're in a position to find the derivative of just about any function you encounter in a single-variable calculus course. Of course, you'll still use the power, product, quotient, and chain rules (Chapters 4 and 5) when finding derivatives.
The Problems You'll Work On
In this chapter, you use implicit differentiation to
· Find the first derivative and second derivative of an implicit function
· Find slopes of tangent lines at given points
· Find equations of tangent lines at given points
What to Watch Out For
Lots of numbers and variables are floating around in these examples, so don't lose your way:
· Don't forget to multiply by dy/dx at the appropriate moment! If you aren't getting the correct solution, look for this mistake.
· After finding the second derivative of an implicitly defined function, substitute in the first derivative in order to write the second derivative in terms of x and y.
· When you substitute the first derivative into the second derivative, be prepared to further simplify.
Using Implicit Differentiation to Find a Derivative
408–413 Use implicit differentiation to find ![]() .
.
408. x2 + y2 = 9
409. y5 + x2y3 = 2 + x2y
410. x3y3 + x cos(y) = 7
411. ![]()
412. 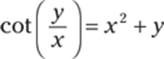
413. ![]()
Using Implicit Differentiation to Find a Second Derivative
414–417 Use implicit differentiation to find ![]() .
.
414. 8 x2 + y2 = 8
415. x5 + y5 = 1
416. x3 + y3 = 5
417. ![]()
Finding Equations of Tangent Lines Using Implicit Differentiation
418–422 Find the equation of the tangent line at the indicated point.
418. x2 + xy + y2 = 3 at (1, 1)
419. ![]() at (2, 1)
at (2, 1)
420. x2 + 2xy + y2 = 1 at (0, 1)
421. cos(xy) + x2 = sin y at ![]()
422. y2(y2 – 1) = x2 tan y at (0, 1)