1,001 Calculus Practice Problems

Part I

The Questions

Chapter 8

What good are derivatives if you can't do anything useful with them? Well, don't worry! There are tons and tons of useful applications involving derivatives. This chapter illustrates how calculus can help solve a variety of practical problems, including finding maximum and minimum values of functions, approximating roots of equations, and finding the velocity and acceleration of an object, just to name a few. Without calculus, many of these problems would be very difficult indeed!

The Problems You'll Work On

This chapter has a variety of applications of derivatives, including

· Approximating values of a function using linearization

· Approximating roots of equations using Newton's method

· Finding the optimal solution to a problem by finding a maximum or minimum value

· Determining how quantities vary in relation to each other

· Locating absolute and local maxima and minima

· Finding the instantaneous velocity and acceleration of an object

· Using Rolle's theorem and the mean value theorem

What to Watch Out For

This chapter presents a variety of applications and word problems, and you may have to be a bit creative when setting up some of the problems. Here are some tips:

· Think about what your variables represent in the optimization and related-rates problems; if you can't explain what they represent, start over!

· You'll have to produce equations in the related-rates and optimization problems. Getting started is often the most difficult part, so just dive in and try different things.

· Remember that linearization is just a fancy way of saying “tangent line.”

· Although things should be set up nicely in most of the problems, note that Newton's method doesn't always work; its success depends on your starting value.

Finding and Evaluating Differentials

423–425 Find the differential dy and then evaluate dy for the given values of x and dx.

423. y = x² – 4x, x = 3,

424. , x = 1, dx = –0.1

425. y = cos² x, , dx = 0.02

Finding Linearizations

426–428 Find the linearization L(x) of the function at the given value of a.

426. f (x) = 3x², a = 1

427. f (x) = cos x + sin x,

428. , a = 2

Using Linearizations to Estimate Values

429–431 Estimate the value of the given number using a linearization.

429. Estimate 7.96^2/3 to the thousandths place.

430. Estimate to the tenths place.

431. Estimate tan 46° to the thousandths place.

Understanding Related Rates

432–445 Solve the related-rates problem. Give an exact answer unless otherwise stated.

432. If V is the volume of a sphere of radius r and the sphere expands as time passes, find in terms of .

433. A pebble is thrown into a pond, and the ripples spread in a circular pattern. If the radius of the circle increases at a constant rate of 1 meter per second, how fast is the area of the circle increasing when the radius is 4 meters?

434. If y = x⁴ + 3x² + x and , find when x = 3.

435. If z³ = x² – y², , and , find when x = 4 and y = 1.

436. Two sides of a triangle are 6 meters and 8 meters in length, and the angle between them is increasing at a rate of 0.12 radians per second. Find the rate at which the area of the triangle is increasing when the angle between the sides is . Round your answer to the nearest hundredth.

437. A ladder 8 feet long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 3 feet per second, how fast is the angle between the top of the ladder and the wall changing when the angle is radians?

438. The base of a triangle is increasing at a rate of 2 centimeters per minute, and the height is increasing at a rate of 4 centimeters per minute. At what rate is the area changing when b = 20 centimeters and h = 32 centimeters?

439. At noon, Ship A is 150 kilometers east of Ship B. Ship A is sailing west at 20 kilometers per hour, and Ship B is sailing north at 35 kilometers per hour. How quickly is the distance between them changing at 3 p.m.? Round your answer to the nearest hundredth.

440. A particle moves along the curve . As the particle passes through the point (8, 3), the x coordinate is increasing at a rate of 5 centimeters per second. How quickly is the distance from the particle to the origin changing at this point? Round your answer to the nearest hundredth.

441. Two people start walking from the same point. One person walks west at 2 miles per hour, and the other walks southwest (at an angle 45° south of west) at 4 miles per hour. How quickly is the distance between them changing after 40 minutes? Round your answer to the nearest hundredth.

442. A trough is 20 feet long, and its ends are isosceles triangles that are 5 feet across the top and have a height of 2 feet. If the trough is being filled with water at a rate of 8 cubic feet per minute, how quickly is the water level rising when the water is 1 foot deep?

443. An experimental jet is flying with a constant speed of 700 kilometers per hour. It passes over a radar station at an altitude of 2 kilometers and climbs at an angle of 45°. At what rate is the distance from the plane to the radar station increasing 2 minutes later? Round your answer to the hundredths place.

444. A lighthouse is located on an island 5 kilometers away from the nearest point P on a straight shoreline, and the light makes 6 revolutions per minute. How fast is the beam of light moving along the shore when it's 2 kilometers from P?

445. Gravel is being dumped into a pile that forms the shape of a cone whose base diameter is twice the height. If the gravel is being dumped at a rate of 20 cubic feet per minute, how fast is the height of the pile increasing when the pile is 12 feet high?

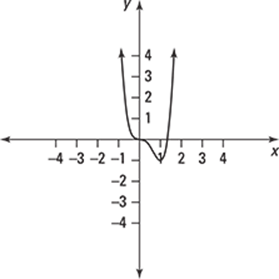
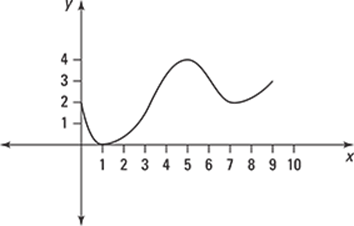
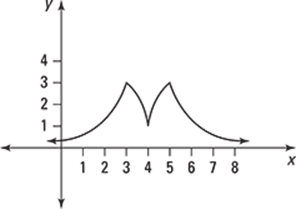
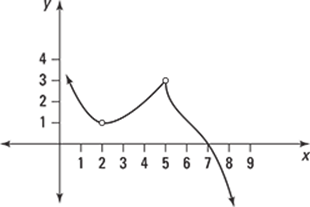
Finding Maxima and Minima from Graphs

446–450 Use the graph to find the absolute maximum, absolute minimum, local maxima, and local minima, if any. Note that endpoints will not be considered local maxima or local minima.

446.

447.

448.

449.

450.

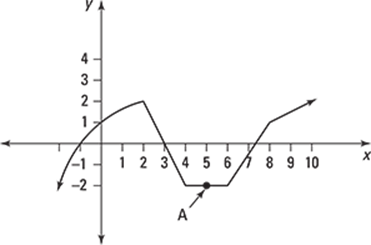
Point A corresponds to which of the following?

I. local maximum

II. local minimum

III. absolute maximum

IV. absolute minimum

Using the Closed Interval Method

451–455 Find the absolute maximum and absolute minimum of the given function using the closed interval method.

451. f (x) = 3x² – 12x + 5 on [0, 3]

452. f (x) = x⁴ – 2x² + 4 on [–2, 3]

453. on [0, 3]

454. on [–1, 2]

455. f (x) = x – 2 cos x on [–π, π]

Finding Intervals of Increase and Decrease

456–460 Find the intervals of increase and decrease, if any, for the given function.

456. f (x) = 2x³ – 24x + 1

457. , x ≥ – 3

458. f (x) = cos² x – sin x on [0, 2π]

459. f (x) = 2 cos x – cos 2x on 0 ≤ x ≤ 2π

460. f (x) = 4 ln x – 2x²

Using the First Derivative Test to Find Local Maxima and Minima

461–465 Use the first derivative to find any local maxima and any local minima.

461. f (x) = 2x³ – 3x² – 12x

462.

463. f (x) = 6x^2/3 – x

464. f (x) = 2 sin x – sin 2x on [0, 2π]

465. f (x) = x + 2 cos x on [–2π, 2π]

Determining Concavity

466–470 Find the intervals where the given function is concave up and concave down, if any.

466. f (x) = x³ – 3x² + 4

467. f (x) = 9x^2/3 – x

468. f (x) = x^1/3(x + 1)

469. f (x) = (x² – 4)³

470. f (x) = 2 cos x – sin(2x) on [0, 2π]

Identifying Inflection Points

471–475 Find the inflection points of the given function, if any.

471.

472. f (x) = 2x³ + x²

473. on [0, 2π]

474. f (x) = 3 sin x – sin³ x on [0, 2π]

475. f (x) = x^5/3 – 5x^2/3

Using the Second Derivative Test to Find Local Maxima and Minima

476–480 Use the second derivative test to find the local maxima and local minima of the given function.

476.

477. f (x) = x⁴ – 4x² + 1

478. f (x) = 2x²(1 – x²)

479.

480. f (x) = 2 sin x – x on [0, 2π]

Applying Rolle's Theorem

481–483 Verify that the function satisfies the hypotheses of Rolle's theorem. Then find all values c in the given interval that satisfy the conclusion of Rolle's theorem.

481. f (x) = x² –6x + 1, [0, 6]

482. , [–8, 0]

483. f (x) = cos(2πx), [–1, 1]

Using the Mean Value Theorem

484–486 Verify that the given function satisfies the hypotheses of the mean value theorem. Then find all numbers c that satisfy the conclusion of the mean value theorem.

484. f (x) = x³ + 3x – 1, [0, 2]

485. , [0, 1]

486. , [1, 4]

Applying the Mean Value Theorem to Solve Problems

487–489 Solve the problem related to the mean value theorem.

487. If f (1) = 12 and f '(x) ≥ 3 for 1 ≤ x ≤ 5, what is the smallest possible value of f (5)? Assume that f satisfies the hypothesis of the mean value theorem.

488. Suppose that 2 ≤ f '(x) ≤ 6 for all values of x. What are the strictest bounds you can put on the value of f (8) – f (4)? Assume that f is differentiable for all x.

489. Apply the mean value theorem to the function f (x) = x^1/3 on the interval [8, 9] to find bounds for the value of .

Relating Velocity and Position

490–492 Use the position function s(t) to find the velocity and acceleration at the given value of t. Recall that velocity is the change in position with respect to time and acceleration is the change in velocity with respect to time.

490. s(t) = t² – 8t + 4 at t = 5

491. s(t) = 2 sin t – cos t at

492. at t = 1

Finding Velocity and Speed

493–497 Solve the given question related to speed or velocity. Recall that velocity is the change in position with respect to time.

493. A mass on a spring vibrates horizontally with an equation of motion given by x(t) = 8 sin(2t), where x is measured in feet and t is measured in seconds. Is the spring stretching or compressing at ? What is the speed of the spring at that time?

494. A stone is thrown straight up with the height given by the function s = 40t – 16t², where s is measured in feet and t is measured in seconds. What is the maximum height of the stone? What is the velocity of the stone when it's 20 feet above the ground on its way up? And what is its velocity at that height on the way down? Give exact answers.

495. A stone is thrown vertically upward with the height given by s = 20t – 16t², where s is measured in feet and t is measured in seconds. What is the maximum height of the stone? What is the velocity of the stone when it hits the ground?

496. A particle moves on a vertical line so that its coordinate at time t is given by y = t³ – 4t + 5 for t ≥ 0. When is the particle moving upward, and when is it moving downward? Give an exact answer in interval notation.

497. A particle moves on a vertical line so that its coordinate at time t is given by y = 4t² – 6t – 2 for t ≥ 0. When is the particle moving upward, and when it is it moving downward? Give your answer in interval notation.

Solving Optimization Problems

498–512 Solve the given optimization problem. Recall that a maximum or minimum value occurs where the derivative is equal to zero, where the derivative is undefined, or at an endpoint (if the function is defined on a closed interval). Give an exact answer, unless otherwise stated.

498. Find two numbers whose difference is 50 and whose product is a minimum.

499. Find two positive numbers whose product is 400 and whose sum is a minimum.

500. Find the dimensions of a rectangle that has a perimeter of 60 meters and whose area is as large as possible.

501. Suppose a farmer with 1,500 feet of fencing encloses a rectangular area and divides it into four pens with fencing parallel to one side. What is the largest possible total area of the four pens?

502. A box with an open top is formed from a square piece of cardboard that is 6 feet wide. Find the largest volume of the box that can be made from the cardboard.

503. A box with an open top and a square base must have a volume of 16,000 cubic centimeters. Find the dimensions of the box that minimize the amount of material used.

504. Find the point(s) on the ellipse 8x² + y² = 8 farthest from (1, 0).

505. Find the point on the line y = 4x + 6 that is closest to the origin.

506. A rectangular poster is to have an area of 90 square inches with 1-inch margins at the bottom and sides and a 3-inch margin at the top. What dimensions give you the largest printed area?

507. At which x values on the curve f (x) = 2 + 20x³ – 4x⁵ does the tangent line have the largest slope?

508. A rectangular storage container with an open top is to have a volume of 20 cubic meters. The length of the base is twice the width. The material for the base costs $20 per square meter. The material for the sides costs $12 per square meter. Find the cost of the materials for the cheapest such container. Round your answer to the nearest cent.

509. A piece of wire that is 20 meters long is cut into two pieces. One is shaped into a square, and the other is shaped into an equilateral triangle. How much wire should you use for the square so that the total area is at a maximum?

510. A piece of wire that is 20 meters long is cut into two pieces. One is bent into a square, and the other is bent into an equilateral triangle. How much wire should you use for the square so that the total area is at a minimum?

511. The illumination of a light source is directly proportional to the strength of the light source and inversely proportional to the square of the distance from the source. Two light sources, one five times as strong as the other, are placed 20 feet apart, and an object is placed on the line between them. How far from the bright light source should the object be placed so that the object receives the least illumination?

512. Find the area of the largest rectangle that can be inscribed in the ellipse .

Doing Approximations Using Newton's Method

513–515 Find the fifth approximation of the root of the equation using the given first approximation.

513. x³ + 4x – 4 = 0 using x₁ = 1. Round the solution to the fifth decimal place.

514. x⁴ – 18 = 0 using x₁ = 2. Round the solution to the seventh decimal place.

515. x⁵ + 3 = 0 using x₁ = –1. Round the answer to the seventh decimal place.

Approximating Roots Using Newton's Method

516–518 Find the root using Newton's method.

516. Use Newton's method to find the root of cos x = x correct to five decimal places.

517. Use Newton's method to find the root of x³ – x² – 2 in the interval [1, 2] correct to five decimal places.

518. Use Newton's method to find the positive root of correct to five decimal places.