1,001 Calculus Practice Problems

Part I

The Questions

Chapter 9

This chapter provides some of the groundwork and motivation for antiderivatives. Finding the area underneath a curve has real-world applications; however, for many curves, finding the area is difficult if not impossible to do using simple geometry. Here, you approximate the area under a curve by using rectangles and then turn to Riemann sums. The problems involving Riemann sums can be quite long and involved, especially because shortcuts to finding the solution do exist; however, the approach used in Riemann sums is the same approach you use when tackling definite integrals. It's worth understanding the idea behind Riemann sums so you can apply that approach to other problems!

The Problems You'll Work On

This chapter presents the following types of problems:

· Using left endpoints, right endpoints, and midpoints to estimate the area underneath a curve

· Finding an expression for the definite integral using Riemann sums

· Expressing a given Riemann sum as a definite integral

· Evaluating definite integrals using Riemann sums

What to Watch Out For

Here are some things to keep in mind as you do the problems in this chapter:

· Estimating the area under a curve typically involves quite a bit of arithmetic but shouldn't be too difficult conceptually. The process should be straightforward after you do a few problems.

· The problems on expressing a given Riemann sum as a definite integral don't always have unique solutions.

· To evaluate the problems involving Riemann sums, you need to know a few summation formulas. You can find them in any standard calculus text if you don't remember them — or you can derive them!

Calculating Riemann Sums Using Left Endpoints

519–522 Find the Riemann sum for the given function with the specified number of intervals using left endpoints.

519. f (x) = 2 + x², 0 ≤ x ≤ 2, n = 4

520. , 1 ≤ x ≤ 4, n = 5. Round your answer to two decimal places.

521. f (x) = 4 ln x + 2x, 1 ≤ x ≤ 4, n = 7. Round your answer to two decimal places.

522. f (x) = e^3x + 4, 1 ≤ x ≤ 9, n = 8. Give your answer in scientific notation, rounded to three decimal places.

Calculating Riemann Sums Using Right Endpoints

523–526 Find the Riemann sum for the given function with the specified number of intervals using right endpoints.

523. f (x) = 1 + 2x, 0 ≤ x ≤ 4, n = 4

524. f (x) = x sin x, 2 ≤ x ≤ 6, n = 5. Round your answer to two decimal places.

525. , 0 ≤ x ≤ 5, n = 6. Round your answer to two decimal places.

526. , 1 ≤ x ≤ 3, n = 8. Round your answer to two decimal places.

Calculating Riemann Sums Using Midpoints

527–530 Find the Riemann sum for the given function with the specified number of intervals using midpoints.

527. f (x) = 2 cos x, 0 ≤ x ≤ 3, n = 4. Round your answer to two decimal places.

528. , 1 ≤ x ≤ 5, n = 5. Round your answer to two decimal places.

529. f (x) = 3e^x + 2, 1 ≤ x ≤ 4, n = 6. Round your answer to two decimal places.

530. , 1 ≤ x ≤ 5, n = 8. Round your answer to two decimal places.

Using Limits and Riemann Sums to Find Expressions for Definite Integrals

531–535 Find an expression for the definite integral using the definition. Do not evaluate.

531.

532.

533.

534.

535.

Finding a Definite Integral from the Limit and Riemann Sum Form

536–540 Express the limit as a definite integral. Note that the solution is not necessarily unique.

536.

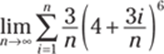
537.

538.

539.

540.

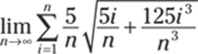
Using Limits and Riemann Sums to Evaluate Definite Integrals

541–545 Use the limit form of the definition of the integral to evaluate the integral.

541.

542.

543.

544.

545.