Advanced Calculus of Several Variables (1973)

Part V. Line and Surface Integrals; Differential Forms and Stokes' Theorem

Chapter 7. THE CLASSICAL THEOREMS OF VECTOR ANALYSIS

In this section we give the classical vector formulations of certain important special cases of the general Stokes’ theorem of Section 6 . The case n = 3, k = 1 yields the original (classical) form of Stokes’ theorem, while the case n= 3, k = 2 yields the “divergence theorem,” or Gauss' theorem.

If F : ⁿ → ⁿ is a vector field with component functions F₁, . . . , F_n, the divergence of F is the real-valued function div F : ⁿ → defined by

The reason for this terminology will be seen in Exercise 7.10. The following result is a restatement of the case k = n − 1 of Stokes' theorem.

Theorem 7.1 Let F be a vector field defined on a neighborhood of the compact oriented smooth n-manifold-with-boundary . Then

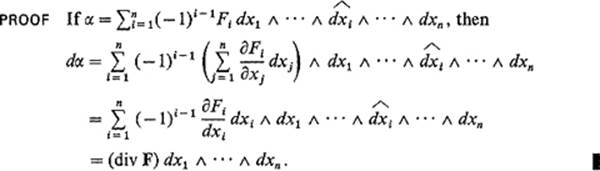
The divergence theorem in ⁿ is the statement that, if F and V are as in Theorem 7.1 , then

where N is the unit outer normal vector field on ∂V, and ∂V is positively oriented (as the boundary of ). The following result will enable us to show that the right-hand side of (2) is equal to the right-hand side of (3) .

Theorem 7.2 Let M be an oriented smooth (n − 1)-manifold in ⁿ with surface area form

Then, for each i = 1, . . . , n, the restrictions to each tangent plane of M, of the differential (n − 1)-forms

are equal.

That is, if the vectors v₁, . . . , v_n−1 are tangent to M at some point x, then

For brevity we write

remembering that we are only asserting the equality of the values of these two differential (n − 1)-forms on (n − 1)-tuples of tangent vectors to M.

PROOF Let v₁, . . . , v_n−1 be tangent vectors to M at the point , and let φ : U → M be an orientation-preserving coordinate patch with . Since the vectors

constitute a basis for the tangent plane to M at x, there exists an (n − 1) × (n − 1) matrix A = (a_ij) such that

If α is any (n − 1)-multilinear function on ⁿ, then

by Exercise 5.15 . It therefore suffices to show that

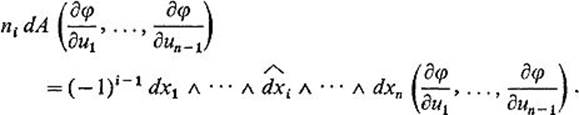
We have seen in Exercise 5.13 that

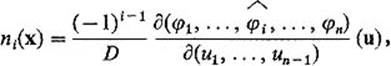
where

Consequently

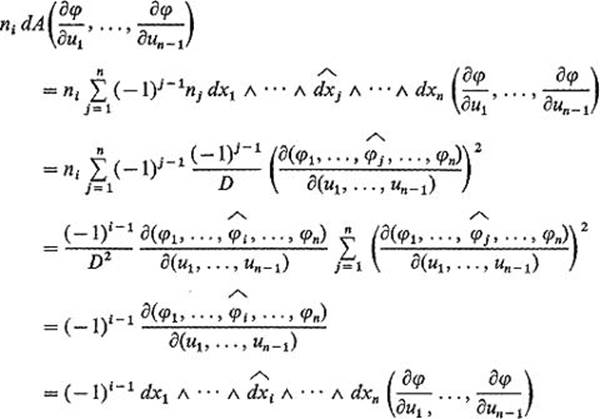
as desired.

In our applications of this theorem, the following interpretation, of the coefficient functions n_i of the surface area form

of the oriented (n −1)-manifold M, will be important. If M is the positively-oriented boundary of the compact oriented n-manifold-with-boundary , then the n_i are simply the components of the unit outer normal vector field Non M = ∂V (see Exercise 6.7) .

Example 1 We consider the case n = 3. If V is a compact 3-manifold-with-boundary in ³, and N = (n₁, n₂, n₃) is the unit outer normal vector field on ∂V, then the surface area form of ∂V is

and Eq. (4) yields

Now let F = (F₁, F₂, F₃) be a vector field in a neighborhood of V. Then Eqs. (6) give

so

Upon combining this equation with Theorem 7.1 , we obtain

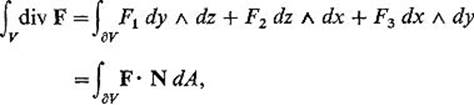
the divergence theorem in dimension 3. Equation (7) , which in essence expresses an arbitrary 2-form on ∂V as a multiple of ∂A, is frequently used in applications of the divergence theorem.

The divergence theorem is often applied to compute a given surface integral by “transforming” it into the corresponding volume integral. The point is that volume integrals are usually easier to compute than surface integrals. The following two examples illustrate this.

Example 2 To compute ∫_∂v x dy dz − y dz dx, we take F = (x, − y, 0). Then div F ≡ 0, so

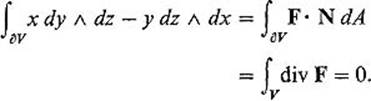
Example 3 To compute , take F = (0, y, xz). Then div F = 1 + x, so

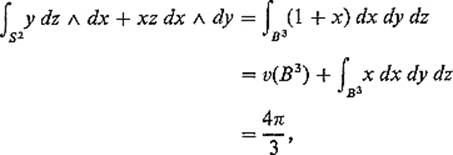
since the last integral is obviously zero by symmetry.

Example 4 Let S₁ and S₂ be two spheres centered at the origin in ³ with S₁ interior to S₂, and denote by R the region between them. Suppose that F is a vector field such that div F = 0 at each point of R. If N₀ is the outer normal vector field on ∂R (pointing outward at each point of S₂, and inward at each point of S₁, as in Fig. 5.42) , then the divergence theorem gives

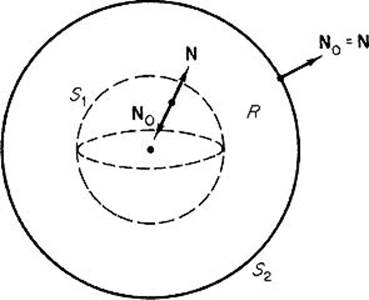
Figure 5.42

If N denotes the outer normal on both spheres (considering each as the positively oriented boundary of a ball), then N = N₀ on S₂, while N = − N₀ on S₁. Therefore

so we conclude that

The proof of the n-dimensional divergence theorem is simply a direct generalization of the proof in Example 1 of the 3-dimensional divergence theorem.

Theorem 7.3 If F is a vector field defined on a neighborhood of the compact n-manifold-with-boundary , then

where N and dA are the outer normal and surface area form of the positively-oriented boundary ∂V.

PROOF In computing the right-hand integral, the (n − 1)-form F · N dA is applied only to (n − 1)-tuples of tangent vectors to ∂V. Therefore we can apply Theorem 7.2 to obtain

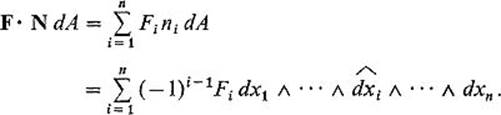
Thus Eq. (3) follows immediately from Theorem 7.1.

The integral ∫_∂v F · N dA is sometimes called the flux of the vector field F across the surface ∂V. This terminology is motivated by the following physical interpretation. Suppose that F = ρv, where v is the velocity vector field of a fluid which is flowing throughout an open set containing V, and ρ is its density distribution function (both functions of x, y, z, and t). We want to show that ∫_∂v F · N dA is the rate at which mass is leaving the region V, that is, that

where

is the total mass of the fluid in V at time T. Let {A₁, . . . , A_k} be an oriented paving of the oriented (n − 1)-manifold ∂V, with the (n − 1)-cells A₁, . . . , A_k so small that each is approximately an (n − 1)-dimensional parallelepiped (Fig. 5.43) . Let N_i, v_i, ρ_i, and F_i = ρ_i v_i be the values of N, v, ρ, and F at a selected point of A_i. Then the volume of that fluid which leaves the region V through the cell A_i, during the short time interval δt, is approximately equal to the volume of an n-dimensional parallelepiped with base A_i and height (v_i δt) · N_i, and the density of this portion of the fluid is approximately ρ_i. Therefore, if δM denotes the change in the mass of the fluid within V during the time interval δt, then

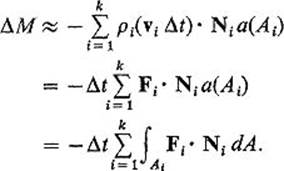
Figure 5.43

Taking the limit as δt → 0, we conclude that

as desired.

We can now apply the divergence theorem to obtain

On the other hand, if ∂ρ/∂t is continuous, then by differentiation under the integral sign we obtain

Consequently

Since this must be true for any region V within the fluid flow, we conclude by the usual continuity argument that

This is the equation of continuity for fluid flow. Notice that, for an incompressible fluid (one for which ρ = constant), it reduces to

We now turn our attention to the special case n = 3, k = 1 which, as we shall see, leads to the following classical formulation of Stokes' theorem in ³:

where D is an oriented compact 2-manifold-with-boundary in ³, N and T are the appropriate unit normal and unit tangent vector fields on D and ∂D, respectively, F = (F₁, F₂, F₃) is a vector field, and curl F is the vector field defined by

This definition of curl F can be remembered in the form

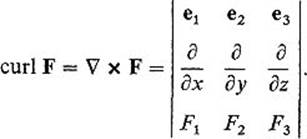
That is, curl F is the result of formal expansion, along its first row, of the 3 × 3 determinant obtained by regarding curl F as the cross product of the gradient operator δ = (∂/∂x, ∂/∂y, ∂/∂z) and the vector F.

If ω = F₁ dx + F₂ dy + F₃ dz is the differential 1-form whose coefficient functions are the components of F, then

by Example 2 of Section 5 . Notice that the coefficient functions of the 2-form dω are the components of the vector curl F. This correspondence, between ω and F on the one hand, and between dω and curl F on the other, is the key to the vector interpretation of Stokes' theorem.

The unit normal N and unit tangent T, in formula (8) above, are defined as follows. The oriented compact 2-manifold-with-boundary D is (by definition) a subset of an oriented smooth 2-manifold . The orientation of Mprescribes a unit normal vector field N on M as in Exercise 5.13 . Specifically,

where φ is an orientation-preserving coordinate patch on M. If n is the outer normal vector field on ∂D—that is, at each point of ∂D, n is the tangent vector to M which points out of D (Fig. 5.44) —then we define the unit tangent on ∂D by

The reader may check “visually” that this definition of T yields the same orientation of ∂D as in the statement of Green's theorem, in case D is a plane region. That is, if one proceeds around ∂D in the direction prescribed by T,remaining upright (regarding the direction of N as “up”), then the region D remains on his left.

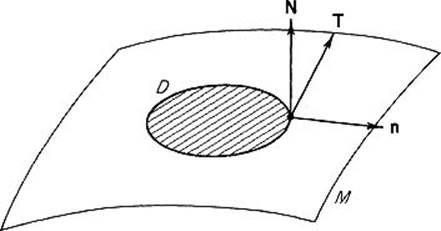
Figure 5.44

Theorem 7.4 Let D be an oriented compact 2-manifold-with-boundary in ³, and let N and T be the unit normal and unit tangent vector fields, on D and ∂D, respectively, defined above. If F is a vector field on an open set containing D, then

PROOF The orientation of ∂D prescribed by (10) is the positive orientation of ∂D, as defined in Section 6. If

it follows that

See Exercise 1.21 or the last paragraph of Section 1 .

Applying Theorem 7.2 in the form of Eq. (6) , we obtain

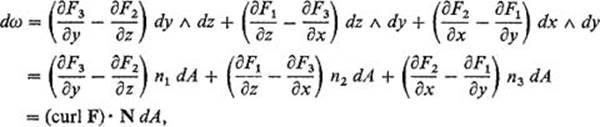
so

Since ∫_D dω = ∫_∂D ω by the general Stokes' theorem, Eqs. (11) and (12) imply Eq. (8) .

Stokes' Theorem is frequently applied to evaluate a given line integral, by “transforming” it to a surface integral whose computation is simpler.

Example 5 Let F(x, y, z) = (x, x + y, x + y + z), and denote by C the ellipse in which the plane z = y intersects the cylinder x² + y² = 1, oriented counterclockwise around the cylinder. We wish to compute ∫_c F · T ds. Let D be the elliptical disk bounded by C. The semiaxes of D are 1 and , so . Its unit normal is , and curl F = (1, −1, 1). Therefore

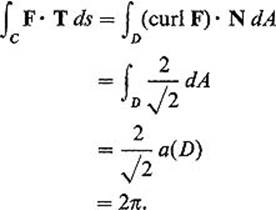
Another typical application of Stokes' theorem is to the computation of a given surface integral by “replacing” it with a simpler surface integral. The following example illustrates this.

Example 6 Let F be the vector field of Example 5 , and let D be the upper hemisphere of the unit sphere S². We wish to compute ∫_D(curl F) · N dA. Let B be the unit disk in the xy-plane, and C = ∂D = ∂B, oriented counterclockwise. Then two applications of Stokes' theorem give

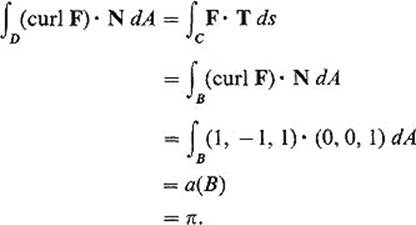
We have interpreted the divergence vector in terms of fluid flow; the curl vector also admits such an interpretation. Let F be the velocity vector field of an incompressible fluid flow. Then the integral

is called the circulation of the field F around the oriented closed curve C. If C_r is the boundary of a small disk D_r of radius r, centered at the point p and normal to the unit vector b (Fig. 5.45) , then

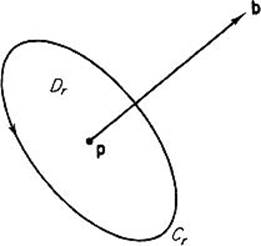
Figure 5.45

Taking the limit as r → 0, we see that

Thus the b-component of curl F measures the circulation (or rotation) of the fluid around the vector b. For this reason the fluid flow is called irrotational if curl F = 0.

For convenience we have restricted our attention in this section to smooth manifolds-with-boundary. However the divergence theorem and the classical Stokes' theorem hold for more general regions. For example, if V is an oriented cellulated n-dimensional region in ⁿ, and F is a vector field, then

(just as in Theorem 7.3), with the following definition of the surface integral on the right. Let be an oriented cellulation of V, and let A₁, . . . , A_p be the boundary (n − 1)-cells of , so . Let A_i be oriented in such a way that the procedure of Exercise 5.13 gives the outer normal vector field on A_i, and denote by N_i this outer normal on A_i. Then we define

We will omit the details, but this more general divergence theorem could be established by the method of proof of the general Stokes' theorem in Section 6—first prove the divergence theorem for an oriented n-cell in ⁿ, and then piece together the n-cells of an oriented cellulation.

Example 7 Let V be the solid cylinder . Denote by D₀ and D₁ the bottom and top disks respectively, and by R the cylindrical surface (Fig. 5.46). Then the outer normal is given by

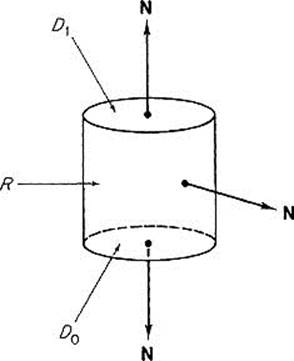
Figure 5.46

If F = (x, y, z), then

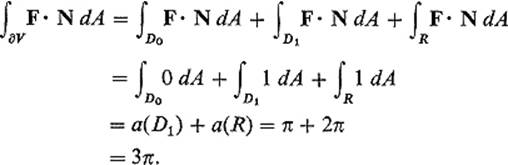
Alternatively, we can apply the divergence theorem to obtain

Similarly, Stokes' theorem holds for piecewise smooth compact oriented surfaces in ³. A piecewise smooth compact oriented surface S in ³ is the union of a collection {A₁, . . . , A_p} of oriented 2-cells in ³, satisfying conditions (b), (c), (d) in the definition of an oriented cellulation (Section 6), with the union ∂S of the boundary edges of these oriented 2-cells being a finite number of oriented closed curves. If F is a vector field, then

(just as in Theorem 7.4), with the obvious definition of these integrals (as in the above discussion of the divergence theorem for cellulated regions). For example, Stokes' theorem holds for a compact oriented polyhedral surface (one which consists of a nonoverlapping triangles).

Exercises

7.1The moment of inertia I of the region about the z-axis is defined by

Show that

7.2Let ρ = (x² + y² + z²)^1/2.

(a)If F(x, y, z) = ρ · (x, y, z), show that div F = 4ρ. Use this fact and the divergence theorem to show that

(B_a³ being the ball of radius a) by converting to a surface integral that can be evaluated by inspection.

(b)If F = ρ² · (x, y, z), compute the integral div F in a similar manner.

7.3Find a function g(ρ) such that, if F(x, y, z) = g(ρ)(x, y, z), then div . Use it to prove that

if V is a compact 3-manifold-with-boundary in ³. For example, show that

7.4In each of the following, let C be the curve of intersection of the cylinder x² + y² = 1 and the given surface z = f(x, y), oriented counterclockwise around the cylinder. Use Stokes' theorem to compute the line integral by first converting it to a surface integral.

(a)

(b)

(c)

7.5Let the 2-form α be defined on ³ − p, p = (a, b, c), by

(a)Show that dα = 0.

(b)Conclude that ∫_M α = 0 if M is a compact smooth 2-manifold not enclosing the point p.

(c)Show that ∫_M α = 4π if M is a sphere centered at p.

(d)Show that ∫_M α = 4π if M is any compact positively oriented smooth 2-manifold enclosing the point p.

7.6The potential φ(x, y, z) at x = (x, y, z) due to a collection of charges q₁, . . . , q_m at the points p₁, . . . , p_m is

where r_i = x − p_i. If E = −φ, the electric field vector, apply the previous problem to show that

if M is a smooth 2-manifold enclosing these charges. This is Gauss' law.

7.7Let f and g be functions on an open set containing the compact n-manifold-with-boundary , and let N be the unit outer normal on ∂V. The Laplacian ²f and the normal derivative ∂f/∂n are defined by

Prove Green's formulas in ⁿ:

(a)

(b)

Hint: For (a), apply the divergence theorem with F = fg.

7.8Use Green's formulas in ⁿ to generalize Exercises 2.7 and 2.8 to ⁿ. In particular, if f and g are both harmonic on and f = g on ∂V, prove that f = g throughout V.

7.9Let f be a harmonic function on the open set . If B is an n-dimensional ball in U with center p and radius a, and S = ∂B, prove that

That is, the value of f at the center of the ball B is the average of its values on the boundary S of B. This is the average value property for harmonic functions. Outline: Without loss of generality, we may assume that p is the origin. Define the function g : ⁿ − 0 → by

Denote by S a small sphere of radius > 0 centered at 0, and by V the region between S and S (Fig. 5.47).

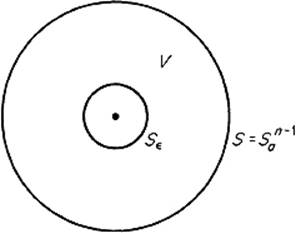
Figure 5.47

(a)Show that g is harmonic, and then apply the second Green's formula (Exercise 7.7) to obtain the formula

(b)Notice that

and similarly for the right-hand side of (*), with a replaced by , because ∂g/∂n = (2 − n)/rⁿ⁻¹. Use the divergence theorem to show that

so formula (*) reduces to

(c)Now obtain the average value property for f by taking the limit in (**) as → 0.

7.10Let F be a vector field in ⁿ. Denote by B the ball of radius centered at p, and S = ∂B. Use the divergence theorem to show that

If we think of F as the velocity vector field of a fluid flow, then this shows that div F(p) is the rate (per unit volume) at which the fluid is “diverging” away from the point p.

7.11Let V be a compact 3-manifold-with-boundary in the lower half-space z < 0 of ³. Think of V as an object submerged in a fluid of uniform density ρ, its surface at z = 0 (Fig. 5.48). The buoyant force B on V, due to the fluid, is defined by

where F = (0, 0, ρz). Use the divergence theorem to show that

Thus the buoyant force on the object is equal to the weight of the fluid that it displaces (Archimedes).

Figure 5.48

7.12Let U be an open subset of ³ that is star-shaped with respect to the origin. This means that, if , then U contains the line segment from 0 to p. Let F be a vector field on U. Then use Stokes' theorem to prove that curl F = 0 on U if and only if

for every polygonal closed curve C in U. Hint: To show that curl F ≡ 0 implies that the integral vanishes, let C consist of the line segments L₁, . . . , L_p. For each i = 1, . . . , p, denote by T_i the triangle whose vertices are the origin and the endpoints of L_i. Apply Stokes' theorem to each of these triangles, and then add up the results.