Advanced Calculus of Several Variables (1973)

Part V. Line and Surface Integrals; Differential Forms and Stokes' Theorem

Chapter 8. CLOSED AND EXACT FORMS

Let ω be a differential k-form defined on the open set U in ⁿ. Then ω is called closed (on U) if dω = 0, and exact (on U) if there exists a (k − 1)-form α on U such that dα = ω.

Since d(dω) = 0 by Proposition 5.1 , we see immediately that every exact form is closed. Our object in this section is to discuss the extent to which the converse is true.

According to Theorem 2.5 , every closed 1-form, which is defined on all of ², is exact. However, we have seen in Section 2 that the 1-form

is closed on ² − 0, but is not exact; that is, there is no function f : ² − 0 → such that df = ω. These facts suggest that the question as to whether the closed 1-form ω on U is exact, depends upon the geometry of the set U.

The “Poincar lemma” (Theorem 8.1 below) asserts that every closed form defined on a star-shaped region is exact. The open set is called star-shaped with respect to the point a provided that, given , the line segment from a to x is contained in U. The open set U is star-shaped if there exists such that U is star-shaped with respect to a. For example, ⁿ itself is star-shaped (with respect to any point), as is every open ball or open n-dimensional interval in ⁿ.

Theorem 8.1 Every closed differential k-form defined on a star-shaped open subset U of ⁿ is exact.

PROOF We may assume (after a translation if necessary) that U is star-shaped with respect to the origin 0. We want to define, for each positive integer k, a certain function I, from k-forms on U to (k − 1)-forms, such that I(0) = 0.

First we need the following notation. Given a k-tuple i = (i₁, i₂, . . . , i_k), write

Note that

and, if ji = (j, i₁, . . . , i_k), then

(Exercise 8.4). Now, given a k-form

on U, we define the (k − 1)-form Iω on U by

Note that this makes sense because U is star-shaped with respect to 0, so if and . Clearly I(0) = 0, and

If ω is closed on U, then

Upon addition of (Eqs. (4) and (5), we obtain

Thus we have found a (k − 1)-form whose differential is ω, as desired.

Example 1 Consider the closed 2-form

on ². In the notation of the proof of Theorem 8.1,

and

Equation (3) therefore gives

a 1-form whose differential is ω.

Theorem 8.1 has as special cases two important facts of vector analysis. Recall that, if F = (P, Q, R) is a vector field on an open set U in ³, then its divergence and curl are defined by

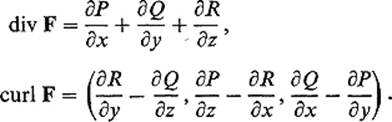
It follows easily that div F = 0 if F = curl G for some vector field G on U, while curl F = 0 if F = grad f = f for some scalar function f. The following theorem asserts that the converses are true if U is star-shaped.

Theorem 8.2 Let F be a vector field on the star-shaped open set . Then

(a)curl F = 0 if and only if there exists f : U → such that F = grad f,

(b)div F = 0 if and only if there exists G : U → ³ such that F = curl G.

PROOF Given a vector field F = (P, Q, R), we define a 1-form α_F, a 2-form β_F, and a 3-form γ_F by

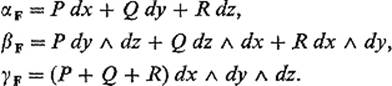
Then routine computations yield the formulas

To prove that curl(grad f) = 0, note that

by (6), (7), and Proposition 5.1 . To prove that div(curl G) = 0, note that

by (7), (8), and Proposition 5.1 .

If curl F = 0 on U, then dα_F = β_{curl F} = 0 by (7), so Theorem 8.1 gives a function f : U → such that df = α_F, that is

so f = F. This proves (a).

If div F = 0 on U, then dβ_F = γ_{div F} = 0 by (8), so Theorem 8.1 gives a 1-form

such that dω = β_F. But if G = (G₁, G₂, G₃), then

by (7), so it follows that curl G = F. This proves (b).

Example 2 As a typical physical application of the Poincar lemma, we describe the reduction of Maxwell‘s electromagnetic field equations to the inhomogeneous wave equation. Maxwell’s equations relate the electric field vector E(x, y, z, t), the magnetic field vector H(x, y, z, t), the charge density ρ(x, y, z), and the current density J(x, y, z); we assume these are all defined on ³ (for each t). With the standard notation div F = · F and curl F = × F, these equations are

Equation (10) asserts that there are no magnetic sources, while (9), (11), and (12) are, respectively, Gauss’ law, Faraday’s law, and Ampere's law.

Let us introduce the following differential forms on ⁴:

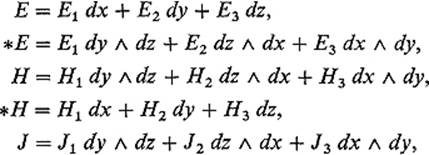
where E = (E₁, E₂, E₃), H = (H₁, H₂, H₃), and J = (J₁, J₂, J₃). Then Eqs. (10) and (11) are equivalent to the equation

while Eqs. (9) and (12) are equivalent to

Thus (13) and (14) are Maxwell's equations in the notation of differential forms.

Because of (13), the Poincar lemma implies the existence of a 1-form

such that

Of course the 1-form α which satisfies (15) is not unique; so does α + df for any differentiable function f : ⁴ → . In particular, if f is a solution of the in-homogeneous wave equation

then the new 1-form

satisfies both the equation

and the condition

Computing dβ, we find that (17) implies that

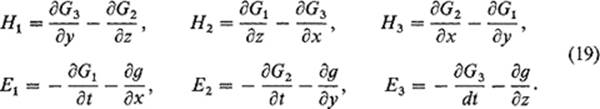
Substituting these expressions for the components of E and H, and making use of (18), a straightforward computation gives

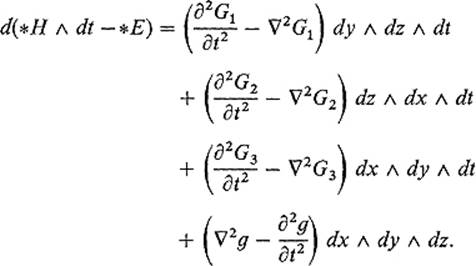
Comparing this result with Eq. (14), we conclude that the vector field G = (G₁, G₂, G₃) on ³ and the function g satisfy the inhomogeneous wave equations

Thus the solution of Maxwell's equations reduces to the problem of solving the inhomogeneous wave equation. In particular, if G and g satisfy Eq. (18) and 20), then the vector fields

defined by Eqs. (19), satisfy Maxwell's equations (9–(12).

Exercises

8.1For each of the following forms ω, find α such that dα = ω.

(a)ω = (3x²y² + 8xy³) dx + (2x³y + 12x²y² + 4y) dy on ².

(b)ω = (y² + 2xz²) dx + (2xy + 3y²z³) dy + (2x²z + 3y³z²) dz on ³.

(c)ω = (2y − 4) dy dz + (y² − 2x) dz dx + (3 − x − 2yz) dx dy.

(d)ω = (xy² + yz² + zx²) dx dy dz.

8.2Let ω be a closed 1-form on ² − 0 such that . Prove that ω is exact on ² − 0. Hint: Given , define f(x, y) to be the integral of ω along the path γ_(x,y) which follows an arc of the unit circle from (1, 0) to (x/ x, yy), and then follows the radial straight line segment to (x, y). Then show that df = ω.

8.3If ω is closed 1-form on ³ − 0, prove that ω is exact on ³ − 0. Hint: Given , define f(p) to be the integral of ω along the path γ_p which follows a great-circle arc on S² from (1, 0, 0) to , and then follows the radial straight line segment to p. Apply Stokes' theorem to show that f(p) is independent of the chosen great circle. Then show that df = ω.

8.4Verify formulas (1) and (2).

8.5Verify formulas (6), (7), and (8).

8.6Let ω = dx + z dy on ³. Given f(x, y, z), compute d(fω). Conclude that ω does not have an integrating factor (see Exercise 5.4).