Advanced Calculus of Several Variables (1973)
Part VI. The Calculus of Variations
Chapter 4. THE ISOPERIMETRIC PROBLEM
In this section we treat the so-called isoperimetric problem that was mentioned in the introduction to this chapter. Given functions f, g : ![]() 3 →
3 → ![]() , we wish to maximize or minimize the function
, we wish to maximize or minimize the function
![]()
subject to the endpoint conditions ψ(a) = α, ψ(b) = β and the constraint
![]()
If, as in Section 3, we denote by M the hyperplane in ![]() consisting of all those
consisting of all those ![]() functions ψ : [a, b] →
functions ψ : [a, b] → ![]() such that ψ(a) = α and
such that ψ(a) = α and ![]() (b) = β, then our problem is to locate the local extrema of the function F on the set
(b) = β, then our problem is to locate the local extrema of the function F on the set ![]() .
.
The similarity between this problem and the constrained maximum–minimum problems of Section II.5 should be obvious—the only difference is that here the functions F and G are defined on the infinite-dimensional normed vector space ![]() , rather than on a finite-dimensional Euclidean space. So our method of attack will be to appropriately generalize the method of Lagrange multipliers so that it will apply in this context.
, rather than on a finite-dimensional Euclidean space. So our method of attack will be to appropriately generalize the method of Lagrange multipliers so that it will apply in this context.
First let us recall Theorem II.5.5 in the following form. Let F, G : ![]() n →
n → ![]() be
be ![]() functions such that G(0) = 0 and ∇G(0) ≠ 0. If F has a local maximum or local minimum at 0 subject to the constraint G(x) = 0, then there exists a number λ such that
functions such that G(0) = 0 and ∇G(0) ≠ 0. If F has a local maximum or local minimum at 0 subject to the constraint G(x) = 0, then there exists a number λ such that
![]()
Since the differentials dF0, dG0 : ![]() n →
n → ![]() are given by
are given by
![]()
Eq. (3) can be rewritten
![]()
where Λ : ![]() →
→ ![]() is the linear function defined by Λ(t) = λt.
is the linear function defined by Λ(t) = λt.
Equation (4) presents the Lagrange multiplier method in a form which is suitable for generalization to normed vector spaces (where differentials are available, but gradient vectors are not). For the proof we will need the following elementary algebraic lemma.
Lemma 4.1 Let α and β be real-valued linear functions on the vector space E such that
![]()
Then there exists a linear function Λ : ![]() →
→ ![]() such that α = Λ
such that α = Λ ![]() β. That is, the following diagram of linear functions “commutes.”
β. That is, the following diagram of linear functions “commutes.”
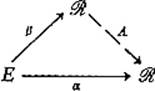
PROOF Given ![]() , pick
, pick ![]() such that β(x) = t, and define
such that β(x) = t, and define
![]()
In order to show that Λ is well defined, we must see that, if y is another element of E with β(y) = t, then α(x) = α(y). But if β(x) = β(y) = t, then ![]()
![]() so α(x − y) = 0, which immediately implies that α(x) = α(y).
so α(x − y) = 0, which immediately implies that α(x) = α(y).
If β(x) = s and β(y) = t, then
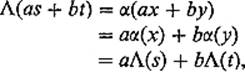
so Λ is linear.
![]()
The following theorem states the Lagrange multiplier method in the desired generality.
Theorem 4.2 Let F and G be real-valued ![]() functions on the complete normed vector space E, with G(0) = 0 and dG0 ≠ 0 (so Im dG0 =
functions on the complete normed vector space E, with G(0) = 0 and dG0 ≠ 0 (so Im dG0 = ![]() ). If F : E →
). If F : E → ![]() has a local extremum at 0 subject to the constraint G(x) = 0, then there exists a linear function λ :
has a local extremum at 0 subject to the constraint G(x) = 0, then there exists a linear function λ : ![]() →
→ ![]() such that
such that
![]()
Of course the statement, that “F has a local extremum at 0 subject to G(x) = 0,” means that the restriction F![]() G−1(0) has a local extremum at
G−1(0) has a local extremum at ![]() .
.
PROOF This will follow from Lemma 4.1, with α = dF0 and β = dG0, if we can prove that Ker dF0 contains Ker dG0. In order to do this, let us first assume the fact (to be established afterward) that, given ![]() , there exists a differentiable path γ : (−
, there exists a differentiable path γ : (−![]() ,
, ![]() ) → E whose image lies in G−1(0), such that γ(0) = 0 and γ′(0) = v (see Fig. 6.6).
) → E whose image lies in G−1(0), such that γ(0) = 0 and γ′(0) = v (see Fig. 6.6).
Then the composition h = F ![]() γ : (−
γ : (−![]() ,
, ![]() ) →
) → ![]() has a local extremum at 0, so h′(0) = 0. The chain rule therefore gives
has a local extremum at 0, so h′(0) = 0. The chain rule therefore gives
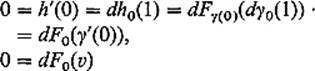
as desired.
We will use the implicit function theorem to verify the existence of the differentiable path γ used above. If X = Ker dG0 then, since dG0 : E → ![]() is continuous, X is a closed subspace of E, and is therefore complete (by Exercise 1.5). Choose
is continuous, X is a closed subspace of E, and is therefore complete (by Exercise 1.5). Choose ![]() such that dG0(w) = 1, and denote by Y the closed subspace of E consisting of all scalar multiples of w; then Y is a “copy” of
such that dG0(w) = 1, and denote by Y the closed subspace of E consisting of all scalar multiples of w; then Y is a “copy” of ![]() .
.
It is clear that ![]() . Also, if
. Also, if ![]() and
and ![]() , then
, then
![]()
so ![]() . Therefore
. Therefore
![]()
with ![]() and
and ![]() . Thus E is the algebraic direct sum of the subspaces X and Y. Moreover, it is true (although we omit the proof) that the norm on E is equivalent to the product norm on X × Y, so we may write E = X × Y.
. Thus E is the algebraic direct sum of the subspaces X and Y. Moreover, it is true (although we omit the proof) that the norm on E is equivalent to the product norm on X × Y, so we may write E = X × Y.
In order to apply the implicit function theorem, we need to know that
![]()
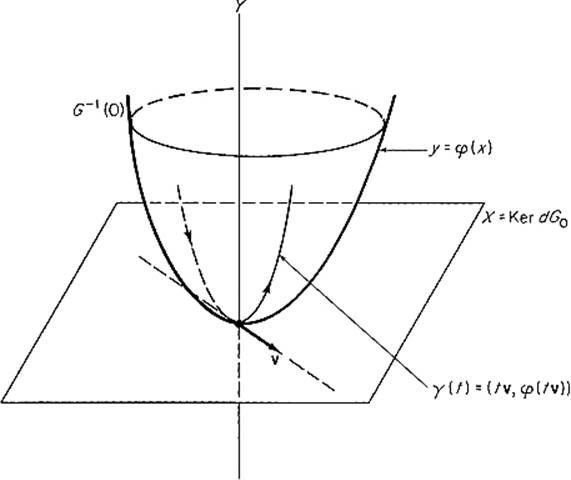
Figure 6.6
is an isomorphism. Since Y ≈ ![]() , we must merely show that dy G0 ≠ 0. But, given
, we must merely show that dy G0 ≠ 0. But, given ![]() , we have
, we have
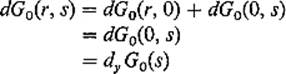
by Exercise 2.6, so the assumption that dy G0 = 0 would imply that dG0 = 0, contrary to hypothesis.
Consequently the implicit function theorem provides a ![]() function φ : X → Y whose graph y = φ(x) in X × Y = E coincides with G−1(0), inside some neighborhood of 0. If H(x) = G(x, φ(x)), then H(x) = 0 for x near 0, so
function φ : X → Y whose graph y = φ(x) in X × Y = E coincides with G−1(0), inside some neighborhood of 0. If H(x) = G(x, φ(x)), then H(x) = 0 for x near 0, so
![]()
for all ![]() . It therefore follows that dφ0 = 0, because dy G0 is an isomorphism.
. It therefore follows that dφ0 = 0, because dy G0 is an isomorphism.
Finally, given ![]() , define γ :
, define γ : ![]() → E by γ(t) = (tu, φ(tu)). Then γ(0) = 0 and
→ E by γ(t) = (tu, φ(tu)). Then γ(0) = 0 and ![]() for t sufficiently small, and
for t sufficiently small, and
![]()
as desired.
![]()
We are now prepared to deal with the isoperimetric problem. Let f and g be real-valued ![]() functions on
functions on ![]() 3, and define the real-valued functions F and G on
3, and define the real-valued functions F and G on ![]() by
by
![]()
and
![]()
where ![]() . Assume that φ is a
. Assume that φ is a ![]() element of
element of ![]() at which F has a local extremum on
at which F has a local extremum on ![]() , where M is the usual hyperplane in
, where M is the usual hyperplane in ![]() that is determined by the endpoint conditions
that is determined by the endpoint conditions ![]() (a) = α and
(a) = α and ![]() (b) = β.
(b) = β.
We have seen (in Section 3) that M is the translate (by any fixed element of M) of the subspace ![]() of
of ![]() consisting of these elements
consisting of these elements ![]() such that
such that ![]() (a) =
(a) = ![]() (b) = 0. Let
(b) = 0. Let ![]() be the translation defined by
be the translation defined by
![]()
and note that T(0) = φ, while
![]()
is the identity mapping.
Now consider the real-valued functions F ![]() T and G
T and G ![]() T on
T on ![]() . The fact that F has a local extremum on
. The fact that F has a local extremum on ![]() at φ implies that F
at φ implies that F ![]() T has a local extremum at 0 subject to the condition G
T has a local extremum at 0 subject to the condition G ![]() T(
T(![]() ) = 0.
) = 0.
Let us assume that φ is not an extremal for G on M, that is, that
![]()
so d(G ![]() T)0 ≠ 0. Then Theorem 4.2 applies to give a linear function Λ :
T)0 ≠ 0. Then Theorem 4.2 applies to give a linear function Λ : ![]() →
→ ![]() such that
such that
![]()
Since dT0 is the identity mapping on C01[a, b], the chain rule gives
![]()
on ![]() . Writing Λ(t) = λt and applying the computation of Corollary 3.2 for the differentials dFφ and dGφ, we conclude that
. Writing Λ(t) = λt and applying the computation of Corollary 3.2 for the differentials dFφ and dGφ, we conclude that
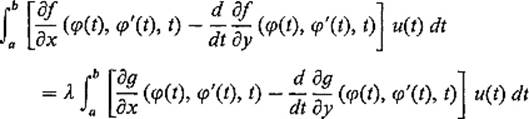
for all ![]() .
.
If h : ![]() 3 →
3 → ![]() is defined by
is defined by
![]()
it follows that
![]()
for all ![]() . An application of Lemma 3.3 finally completes the proof of the following theorem.
. An application of Lemma 3.3 finally completes the proof of the following theorem.
Theorem 4.3 Let F and G be the real-valued functions on ![]() defined by (6) and (7), where f and g are
defined by (6) and (7), where f and g are ![]() functions on
functions on ![]() 3. Let
3. Let ![]() be a
be a ![]() function which is not an extremal for G. If F has a local extremum at φ subject to the conditions
function which is not an extremal for G. If F has a local extremum at φ subject to the conditions
![]()
then there exists a real number λ such that φ satisfies the Euler–Lagrange equation for the function h = f − λg, that is,
![]()
for all ![]() .
.
The following application of this theorem is the one which gave such constraint problems in the calculus of variations their customary name—isoperimetric problems.
Example Suppose φ : [a, b] → ![]() is that nonnegative function (if any) with φ(a) = φ(b) = 0 whose graph x = φ(t) has length L, such that the area under its graph is maximal. We want to prove that the graph x = φ(t) must be an arc of
is that nonnegative function (if any) with φ(a) = φ(b) = 0 whose graph x = φ(t) has length L, such that the area under its graph is maximal. We want to prove that the graph x = φ(t) must be an arc of
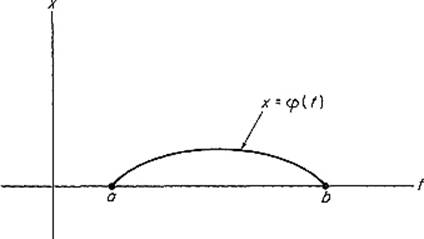
Figure 6.7
a circle (Fig. 6.7). If f(x, y, t) = x and ![]() , then φ maximizes the integral
, then φ maximizes the integral
![]()
subject to the conditions
![]()
Since ![]() , the Euler-Lagrange equation (8) is
, the Euler-Lagrange equation (8) is
![]()
or
![]()
This last equation just says that the curvature of the curve t → (t, φ(t)) is the constant 1/λ. Its image must therefore be part of a circle.
The above discussion of the isoperimetric problem generalizes in a straightforward manner to the case in which there is more than one constraint. Given ![]() functions f, g1, . . . , gk:
functions f, g1, . . . , gk: ![]() 3 →
3 → ![]() , we wish to minimize or maximize the function
, we wish to minimize or maximize the function
![]()
subject to the endpoint conditions ![]() (a) = α,
(a) = α, ![]() (b) = β and the constraints
(b) = β and the constraints
![]()
Our problem then is to locate the local extrema of F on ![]() , where M is the usual hyperplane in
, where M is the usual hyperplane in ![]() and
and
![]()
The result, analogous to Theorem 4.3, is as follows.
Let ![]() be a
be a ![]() function which is not an extremal for any linear combination of the functions G1, . . . , Gk. If F has a local extremum at φ subject to the conditions
function which is not an extremal for any linear combination of the functions G1, . . . , Gk. If F has a local extremum at φ subject to the conditions
![]()
then there exist numbers λ1, . . . , λk such that φ satisfies the Euler–Lagrange equation for the function
![]()
Inclusion of the complete details of the proof would be repetitious, so we simply outline the necessary alterations in the proof of Theorem 4.3.
First Lemma 4.1 and Theorem 4.2 are slightly generalized as follows. In Lemma 4.1 we take β to be a linear mapping from E to ![]() k with Im β =
k with Im β = ![]() k, and in Theorem 4.2 we take G to be a
k, and in Theorem 4.2 we take G to be a ![]() mapping from E to
mapping from E to ![]() k such that G(0) = 0 and Im dG0 =
k such that G(0) = 0 and Im dG0 = ![]() k. The only other change is that, in the conclusion of each, Λ becomes a real-valued linear function on
k. The only other change is that, in the conclusion of each, Λ becomes a real-valued linear function on ![]() k. The proofs remain essentially the same.
k. The proofs remain essentially the same.
We then apply the generalized Theorem 4.2 to the mappings ![]() and
and ![]() , defined by (9) and (10), in the same way that the original (Theorem 4.2) was applied (in the proof of Theorem 4.3) to the functions defined by (6) and (7). The only additional observation needed is that, if φ is not an extremal for any linear combination of the component functions G1, . . . , Gk, then it follows easily that dGφ maps TMφ onto
, defined by (9) and (10), in the same way that the original (Theorem 4.2) was applied (in the proof of Theorem 4.3) to the functions defined by (6) and (7). The only additional observation needed is that, if φ is not an extremal for any linear combination of the component functions G1, . . . , Gk, then it follows easily that dGφ maps TMφ onto ![]() k. We then conclude as before that
k. We then conclude as before that
![]()
for some linear function Λ : ![]() k →
k → ![]() . Writing
. Writing ![]() , we conclude that
, we conclude that
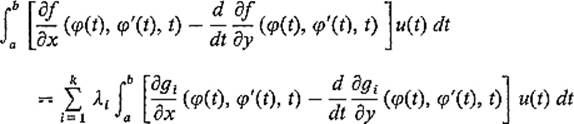
for all ![]() . An application of Lemma 3.3 then implies that φ satisfies the Euler–Lagrange equation for
. An application of Lemma 3.3 then implies that φ satisfies the Euler–Lagrange equation for ![]() .
.
Exercises
4.1Consulting the discussion at the end of Section 3, generalize the isoperimetric problem to the vector-valued case as follows: Let f, g : ![]() n ×
n × ![]() n ×
n × ![]() →
→ ![]() be given functions, and suppose φ : [a, b] →
be given functions, and suppose φ : [a, b] → ![]() n is an extremal for
n is an extremal for
![]()
subject to the conditions ![]() (a) = α,
(a) = α, ![]() (b) = β and
(b) = β and
![]()
Then show under appropriate conditions that, for some number λ, the path φ satisfies the Euler–Lagrange equations
![]()
for the function h = f − λg.
4.2Let φ : [a, b] → ![]() 2 be a closed curve in the plane, φ(a) = φ(b), and write φ(t) = (x(t), y(t)). Apply the result of the previous problem to show that, if φ maximizes the area integral
2 be a closed curve in the plane, φ(a) = φ(b), and write φ(t) = (x(t), y(t)). Apply the result of the previous problem to show that, if φ maximizes the area integral
![]()
subject to
![]()
then the image of φ is a circle.
4.3With the notation and terminology of the previous problem, establish the following reciprocity relationship. The closed path φ is an extremal for the area integral, subject to the arclength integral being constant, if and only if φ is an extremal for the arclength integral subject to the area integral being constant. Conclude that, if φ has minimal length amongst curves enclosing a given area, then the image of φ is a circle.
4.4Formulate (along the lines of Exercise 3.9) a necessary condition that φ : [a, b] → ![]() minimize
minimize
![]()
subject to
![]()
This is the isoperimetric problem with second derivatives.
4.5Suppose that ![]() describes (in polar coordinates) a closed curve of length L that encloses maximal area. Show that it is a circle by maximizing
describes (in polar coordinates) a closed curve of length L that encloses maximal area. Show that it is a circle by maximizing
![]()
subject to the condition
![]()
4.6A uniform flexible cable of fixed length hangs between two fixed points. If it hangs in such a way as to minimize the height of its center of gravity, show that its shape is that of a catenary (see Example 2 of Section 3). Hint: Note that Exercise 3.2 applies.
4.7If a hanging flexible cable of fixed length supports a horizontally uniform load, show that its shape is that of a parabola.