Advanced Calculus of Several Variables (1973)

Part I. Euclidean Space and Linear Mappings

Chapter 5. THE KERNEL AND IMAGE OF A LINEAR MAPPING

Let L : V → W be a linear mapping of vector spaces. By the kernel of L, denoted by Ker L, is meant the set of all those vectors such that

By the image of L, denoted by Im L or f(L), is meant the set of all those vectors such that w = L(v) for some vector ,

It follows easily from these definitions, and from the linearity of L, that the sets Ker L and Im L are subspaces of V and W respectively (Exercises 5.1 and 5.2). We are concerned in this section with the dimensions of these subspaces.

Example 1If a is a nonzero vector in ⁿ, and L : ⁿ → is defined by L(x) = a · x, then Ker L is the (n − 1)-dimensional subspace of ⁿ that is orthogonal to the vector a, and Im L = .

Example 2If P : ³ → ² is the projection P(x₁, x₂, x₃) = (x₁, x₂), then Ker P is the x₃-axis and Im P = ².

The assumption that the kernel of L : V → W is the zero vector alone, Ker L = 0, has the important consequence that L is one-to-one, meaning that L(v₁) = L(v₂) implies that v₁ = v₂ (that is, L is one-to-one if no two vectors of Vhave the same image under L).

Theorem 5.1Let L : V → W be linear, with V being n-dimensional. If Ker L = 0, then L is one-to-one, and Im L is an n-dimensional subspace of W.

PROOFTo show that L is one-to-one, suppose L(v₁) = L(v₂). Then L(v₁ − v₂) = 0, so v₁ − v₂ = 0 since Ker L = 0.

To show that the subspace Im L is n-dimensional, start with a basis v₁, . . . , v_n for V. Since it is clear (by linearity of L) that the vectors L(v₁), . . . , L(v_n) generate Im L, it suffices to prove that they are linearly independent. Suppose

Then

so t₁v₁ + · · · + t_n v_n = 0 because Ker L = 0. But then t₁ = · · · = t_n = 0 because the vectors v₁, . . . , v_n are linearly independent.

An important special case of Theorem 5.1 is that in which W is also n-dimensional; it then follows that Im L = W (see Exercise 5.3).

Theorem 5.2Let L : ⁿ → ^m be defined by L(x) = Ax, where A = (a_ij) is an m × n matrix. Then

(a)Ker L is the orthogonal complement of that subspace of ⁿ that is generated by the row vectors A₁, . . . , A_m of A, and

(b)Im L is the subspace of ^m that is generated by the column vectors A¹, . . . , Aⁿ of A.

PROOF(a) follows immediately from the fact that L is described by the scalar equations

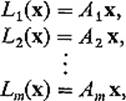
so that the ith coordinate L_i(x) is zero if and only if x is orthogonal to the row vector A_i.

(b) follows immediately from the fact that Im L is generated by the images L(e₁), . . . , L(e_n) of the standard basis vectors in ⁿ, whereas L(e_i) = Aⁱ, i = 1, . . . , n, by the definition of matrix multiplication.

Example 3Suppose that the matrix of L : ³ → ³ is

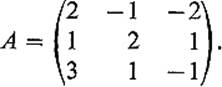
Then A₃ = A₁ + A₂, but A₁ and A₂ are not collinear, so it follows from 5.2(a) that Ker L is 1-dimensional, since it is the orthogonal complement of the 2-dimensional subspace of ³ that is spanned by A₁ and A₂. Since the column vectors of A are linearly dependent, 3A¹ = 4A² − 5A³, but not collinear, it follows from 5.2(b) that Im L is 2-dimensional.

Note that, in this example, dim Ker L + dim Im L = 3. This is an illustration of the following theorem.

Theorem 5.3If L : V → W is a linear mapping of vector spaces, with dim V = n, then

PROOFLet w₁, . . . , w_p be a basis for Im L, and choose vectors such that L(v_i) = w_i for i = 1, . . . , p. Also let u₁, . . . , u_q be a basis for Ker L. It will then suffice to prove that the vectors v₁, . . . , v_p, u₁, . . . , u_q constitute a basis for V.

To show that these vectors generate V, consider . Then there exist numbers a₁, . . . , a_p such that

because w₁, . . . , w_p is a basis for Im L. Since w_i = L(v_i) for each i, by linearity we have

or

so . Hence there exist numbers b₁, . . . , b_q such that

or

as desired.

To show that the vectors v₁, . . . , v_p, u₁, . . . , u_q are linearly independent, suppose that

Then

because L(v_i) = w_i and L(u_j) = 0. Since w₁, . . . , w_p are linearly independent, it follows that s₁ = · · · = s_p = 0. But then t₁u₁ + · · · + t_q u_q = 0 implies that t₁ = · · · = t_q = 0 also, because the vectors u₁, . . . , u_q are linearly independent. By Proposition 2.1 this concludes the proof.

We give an application of Theorem 5.3 to the theory of linear equations. Consider the system

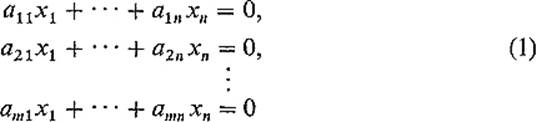
of homogeneous linear equations in x₁, . . . , x_n. As we have observed in Example 9 of Section 3, the space S of solutions (x₁, . . . , x_n) of (1) is the orthogonal complement of the subspace of ⁿ that is generated by the row vectors of the m × n matrix A = (a_ij). That is,

where L : ⁿ → ^m is defined by L(x) = Ax (see Theorem 5.2).

Now the row rank of the m × n matrix A is by definition the dimension of the subspace of ⁿ generated by the row vectors of A, while the column rank of A is the dimension of the subspace of ^m generated by the column vectors of A.

Theorem 5.4 The row rank of the m × n matrix A = (a_ij) and the column rank of A are equal to the same number r. Furthermore dim S = n − r, where S is the space of solutions of the system (1) above.

PROOFWe have observed that S is the orthogonal complement to the subspace of ⁿ generated by the row vectors of A, so

by Theorem 3.4. Since S = Ker L, and by Theorem 5.2, Im L is the subspace of ^m generated by the column vectors of A, we have

by Theorem 5.3. But Eqs. (2) and (3) immediately give the desired results.

Recall that if U and V are subspaces of ⁿ, then

and

are both subspaces of ⁿ (Exercises 1.2 and 1.3). Let

Then U × V is a subspace of ²ⁿ with dim(U × V) = dim U + dim V (Exercise 5.4).

Theorem 5.5If U and V are subspaces of ⁿ, then

In particular, if U + V = ⁿ, then

PROOFLet L : U × V → ⁿ be the linear mapping defined by

Then Im L = U + V and so dim Im L = dim(U + V) and dim Since dim U × V = dim U + dim V by the preceding remark, Eq. (4) now follows immediately from Theorem 5.3.

Theorem 5.5 is a generalization of the familiar fact that two planes in ³ “generally” intersect in a line (“generally” meaning that this is the case if the two planes together contain enough linearly independent vectors to span ³). Similarly a 3-dimensional subspace and a 4-dimensional subspace of ⁷ generally intersect in a point (the origin); two 7-dimensional subspaces of ¹⁰ generally intersect in a 4-dimensional subspace.

Exercises

5.1If L : V → W is linear, show that Ker L is a subspace of V.

5.2If L : V → W is linear, show that Im L is a subspace of W.

5.3Suppose that V and W are n-dimensional vector spaces, and that F : V → W is linear, with Ker F = 0. Then F is one-to-one by Theorem 5.1. Deduce that Im F = W, so that the inverse mapping G = F⁻¹ : W → V is defined. Prove that G is also linear.

5.4If U and V are subspaces of ⁿ, prove that is a subspace of ²ⁿ, and that dim(U × V) = dim U + dim V. Hint: Consider bases for U and V.

5.5Let V and W be n-dimensional vector spaces. If L : V → W is a linear mapping with Im L = W, show that Ker L = 0.

5.6Two vector spaces V and W are called isomorphic if and only if there exist linear mappings S : V → W and T : W → V such that S T and T S are the identity mappings of W and V respectively. Prove that two finite-dimensional vector spaces are isomorphic if and only if they have the same dimension.

5.7Let V be a finite-dimensional vector space with an inner product , . The dual space V^* of V is the vector space of all linear functions V → . Prove that V and V^* are isomorphic. Hint: Let v₁, . . . , v_n be an orthonormal basis for V, and define by θ_j(v_i) = 0 unless i = j, θ_j(v_j) = 1. Then prove that θ₁, . . . , θ_n constitute a basis for V^*.