High School Algebra I Unlocked (2016)
Chapter 8. Quadratic Functions
Lesson 8.2. Solving Quadratic Functions
Let’s begin by breaking down a quadratic and discussing some key features of quadratic functions. Consider the example f(x) = x2 − 5x + 6. Start with the stuff you already know how to do: Create a table of the inputs and outputs and graph the function.
|
f(x) = x2 − 5x + 6 |
|
|
Input: (x) |
Output: f(x) |
|
0 |
6 |
|
1 |
2 |
|
2 |
0 |
|
3 |
0 |
|
4 |
2 |
Based on the table, you can graph the function in the coordinate plane:
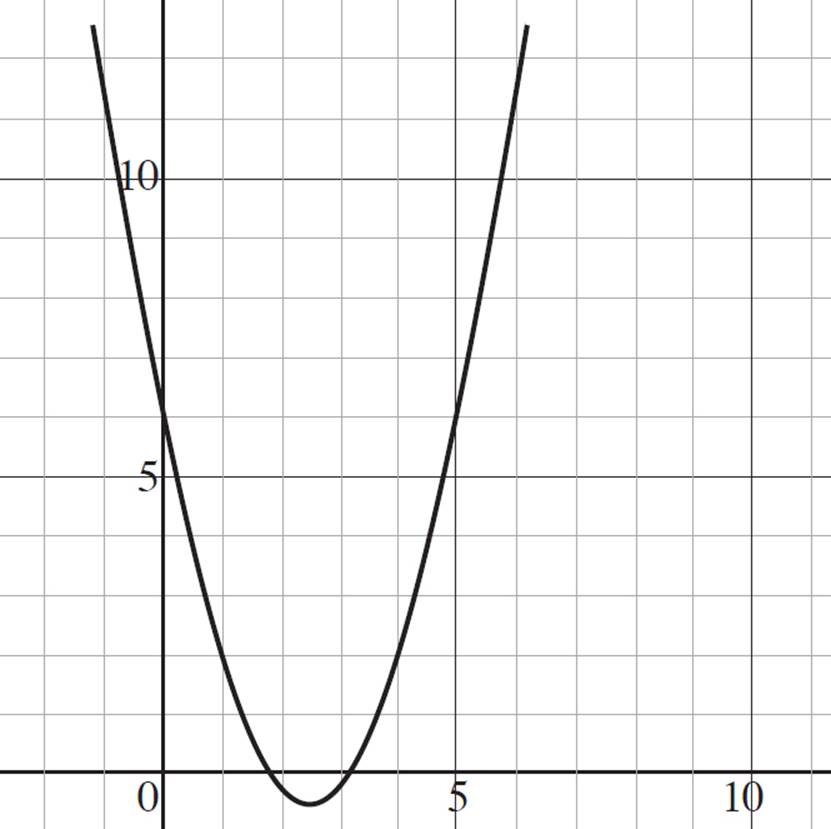

Refer back to
Lesson 5.1 for a
referesher on finding
x- and y-intercepts.
You can also find the x- and y-intercepts of the quadratic. To find the x-intercepts, or roots, of the quadratic, set x2 − 5x + 6 equal to zero and factor. Based on the rules for factoring quadratics in the standard form ax2 + bx + c, if the value of the c-term is positive and the value of b-term is negative, the factors m and n, whose product is c, will both be negative. Thus, our chart of potential factors would look like this:
|
Factors of c-term (6) |
Sum of the Factors |
Value of b-term (−5) |
|
−1, −6 |
−1 + (−6) = −7 |
−5 |
|
−2, −3 |
−2 + (−3) = −5 |
−5 |
According to the chart, the only factors of the c-term, 6, that add up to the b-term, −5, are −2 and −3. Therefore, we can factor the quadratic as follows:
x2 − 5x + 6 = (x − 2)(x − 3)
Now that you’ve factored the quadratic, use the zero product property to find the values of x:
|
(x − 2) |
(x − 3) |
|
x − 2 = 0 |
x − 3 = 0 |
|
x = 2 |
x = 3 |
Thus, the x-intercepts of the quadratic f(x) = x2 − 5x + 6 are (2, 0) and (3, 0).
Next, find the y-intercept by setting x = 0 and solving for f(x) in f(x) = x2 − 5x + 6:
f(x) = 0 − 0 + 6
f(x) = 6
Thus, the y-intercept of f(x) = x2 − 5x + 6 is (0, 6). Label the intercepts on the graph, as shown on the next page.
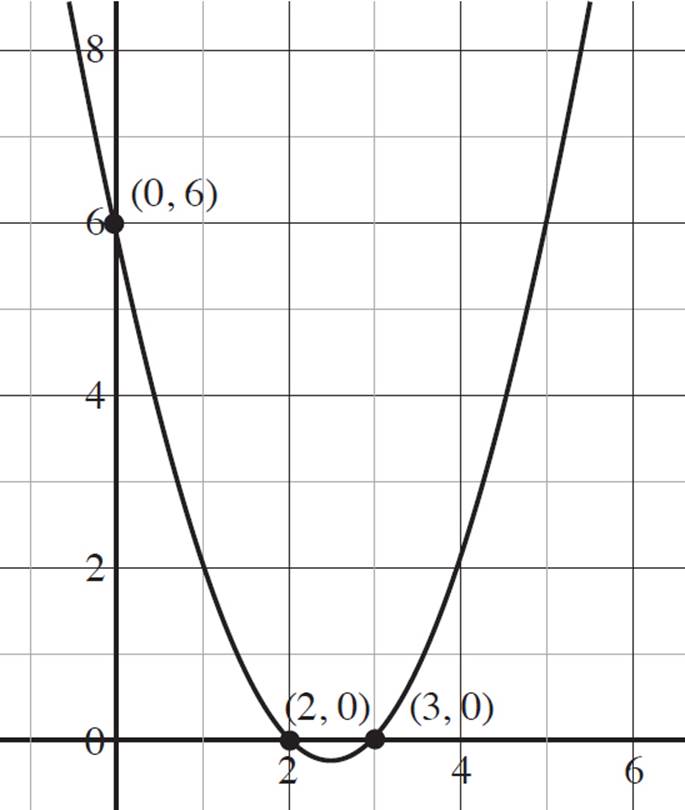
You’ll also need to know how to find the vertex and the axis of symmetry of a quadratic function. Both the vertex and the axis of symmetry are found by using portions of the quadratic formula. And, once again, you find this information about quadratics functions in the same way that you do quadratic equations. Let’s refresh our memory and review these concepts.
The quadratic formula is x = 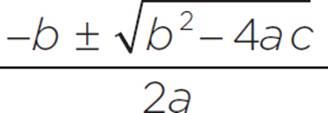 .
.
The vertex (h, k) for any quadratic ax2 + bx + c can be determined with (h, k) = (−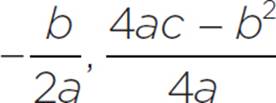 ).
).
The axis of symmetry for any quadratic ax2 + bx + c can be determined with x = −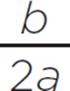 .
.
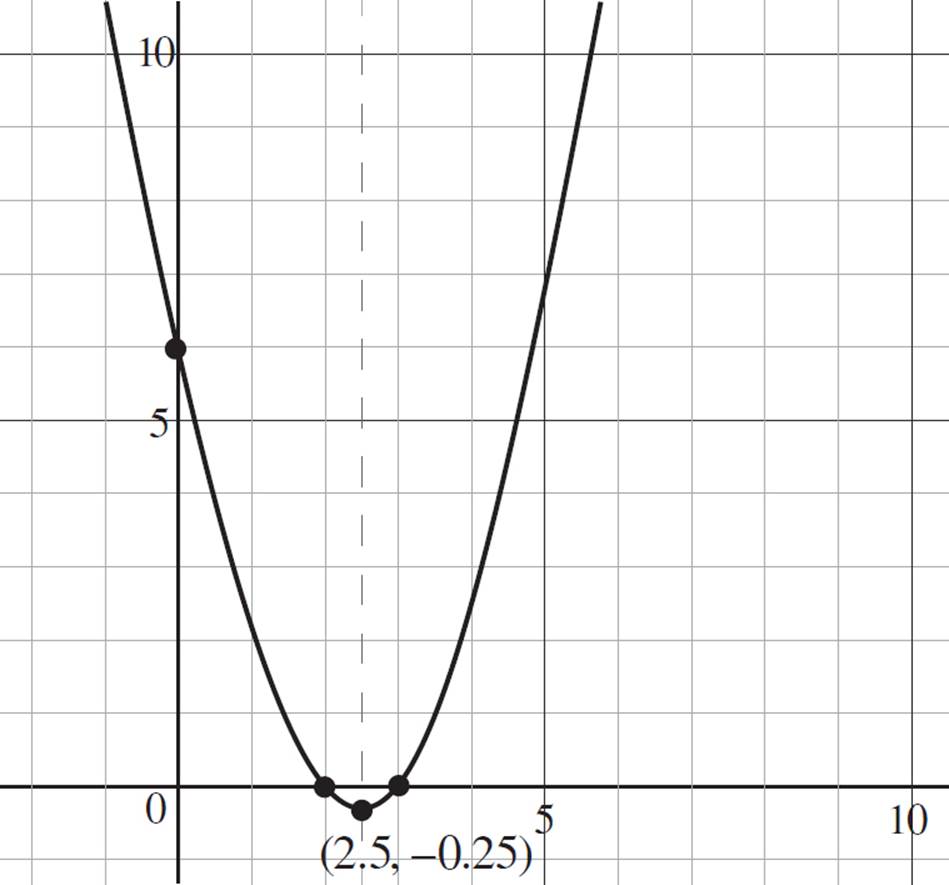
Let’s start by finding the vertex of our quadratic function, f(x) = x2 − 5x + 6, where a = 1, b = −5, and c = 6.
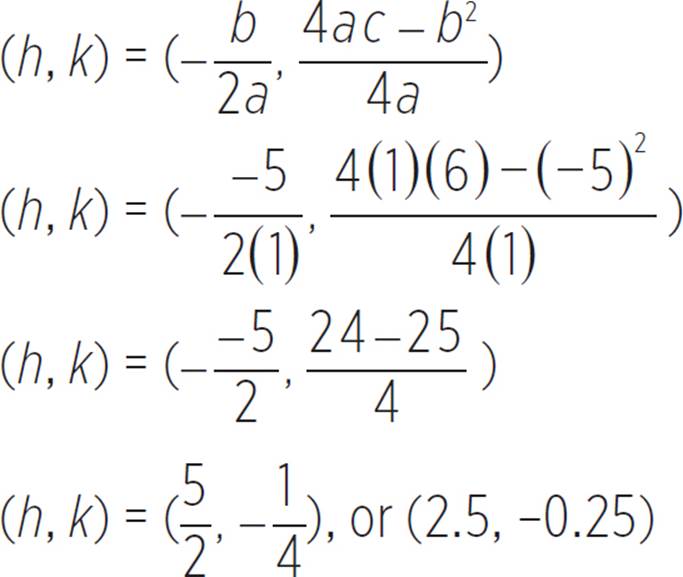
Thus, the vertex of the function f(x) = x2 − 5x + 6 is (h, k) = (2.5, −0.25). Now let’s find the axis of symmetry.
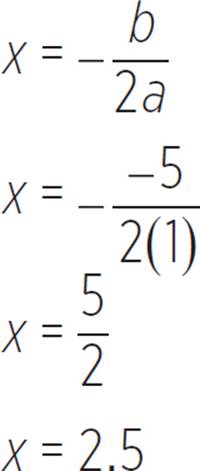
Therefore, the axis of symmetry is found at x = 2.5 (or 5/2). You may have noticed that you had already found the value of −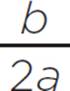 when you solved for the vertex of the function; If you did, well played! You do not need to solve for the same value twice, so you can save yourself some time if you remember this trick in the future.
when you solved for the vertex of the function; If you did, well played! You do not need to solve for the same value twice, so you can save yourself some time if you remember this trick in the future.
You will also be asked to find the minimum or the maximum of a quadratic function, which is closely related to both the vertex and the axis of symmetry. In order to determine whether you are looking for a minimum or a maximum value, you need to consider the value of a when the quadratic function is in standard form, f(x) = ax2 + bx + c. If the value of a < 0, you are looking for a maximum value, but if a > 0, you are looking for a minimum value. In our function, f(x) = x2− 5x + 6, since a > 0 and the axis of symmetry occurs at x = −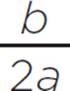 = 2.5, the minimum value of this function occurs at x = 2.5.
= 2.5, the minimum value of this function occurs at x = 2.5.
Minimum and Maximum
Given a quadratic function is in standard form, f(x) = ax2 + bx + c:
If a > 0, the quadratic will have a minimum value at x = −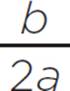 .
.
If a < 0, the quadratic will have a maximum value at x = −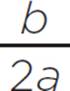 .
.
We can indicate the vertex, which is also the minimum value, and the axis of symmetry, shown with a dashed line, on our graph:
You can also determine the domain and range of a quadratic function. Recall that the domain of a function is all possible x-values for which the function exists, while the range of a function is all possible y-values for which the function exists.
Parabola Behavior
Given a quadratic function is in standard form, f(x) = ax2 + bx + c:
If a > 0, f(x) → ∞ when x → ∞ or x → −∞.
If a < 0, f(x) → −∞ when x → ∞ or x → −∞.
Looking at the graph of f(x) = x2 − 5x + 6, the function continues to both the left and right indefinitely. Therefore, the domain of the function is all real numbers, −∞ < x < ∞; this is expressed in interval notation as (−∞, ∞). Now look at the possible y-values for the function. The minimum y-value occurs at −0.25, and the graph continues upwards indefinitely. Thus, the range of the function is −0.25 ≤ y < ∞, which is expressed in interval notation as [−0.25, ∞).
In addition to the domain and range of a function, you may be asked to determine the intervals of increase and decrease of a function.
Intervals of Increase and Decrease
A quadratic function is increasing if the function slopes upwards from left to right along the x-axis.
A quadratic function is decreasing if the function slopes downwards from left to right along the x-axis.
Therefore, the function f(x) = x2 − 5x + 6 is decreasing from (−∞, 2.5] and increasing from [2.5, ∞).
When expressing
intervals of increase
or decrease along
the x-axis, you must
express your answer
using open intervals;
that is, express
the intervals using
parentheses rather
than brackets.

Here is how you may see quadratic functions on the SAT.
Which of the following shows the graph of y = 2(x − 2)2 + 3 ?
A) 
B) 
C) 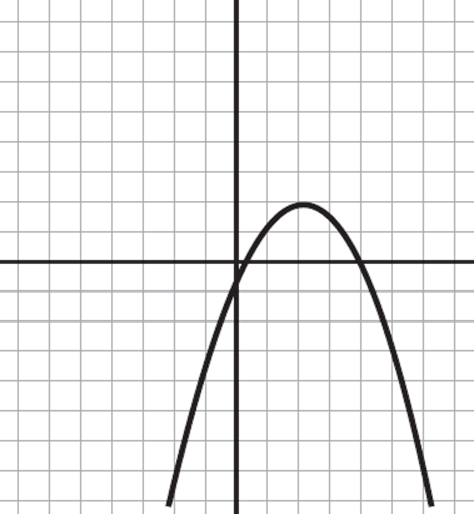
D) 
One final bit of information that you should know about is the end behavior of a function, which is the behavior of f(x) as x approaches either positive or negative infinity. Essentially, you’re describing what happens to the function at the two tail ends of the parabola.
Consider the left end the function f(x) = x2 − 5x + 6. As the value of x approaches negative infinity, the value of f(x), or y, approaches infinity. Looking at the right end of the function, as the value of x approaches infinity, so does the value of f(x), or y. We would express the end behavior as follows:
f(x) → ∞, as x → −∞
f(x) → ∞, as x → ∞
Congratulations! You have successfully tackled the function f(x) = x2 − 5x + 6 and know more about this function than you probably ever wanted to. Now it’s time to try some questions.
EXAMPLE 
Find the discriminant to determine the number of real solutions in the function f(x) = −10x2 − 4x − 2. If real solutions exist, find the x- and y-intercepts, the vertex, axis of symmetry, domain, and range of the function.
This question may look a little different to you, but you did similar questions when you worked with quadratic equations in Chapter 6. To determine the number of real solutions of a quadratic function, you need to use the discriminant: b2 − 4ac. If positive, the quadratic has two real solutions; if zero, the quadratic has one real solution; and if negative, the quadratic has no real solutions, but two complex solutions. Since the function f(x) = −10x2 − 4x − 2 is already in standard form, we know that a = −10, b = −4, andc = −2, and we can plug these values into the discriminant:
b2 − 4ac = (−4)2 − 4(−10)( −2)
= 16 − 80
= −64
As you can see, the discriminant is negative. Thus, the quadratic has no real solutions and instead has two complex solutions. And since there are no real solutions, you’re done with the question!

EXAMPLE 
Use the discriminant to determine the number of real solutions in the function f(x) = 2x(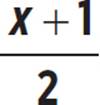 ) − 72.
) − 72.
If real solutions exist, factor the quadratic to find the x-intercepts. Then solve for the vertex, find the axis of symmetry, determine whether the function has a minimum or maximum value, and state the intervals of increase and decrease. Finally, graph the function and label the vertex and axis of symmetry in the coordinate plane.
Here you have another question that asks you to find several pieces of information. Don’t get overwhelmed—just attack each part of the question in turn.
First, figure out if the quadratic has any real solutions by finding the value of the discriminant. Since the function f(x) = 2x(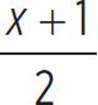 ) − 72 is not in standard form, start by expanding the function and putting it standard form: f(x) = ax2 + bx + c. When you expand the function, you find that
) − 72 is not in standard form, start by expanding the function and putting it standard form: f(x) = ax2 + bx + c. When you expand the function, you find that
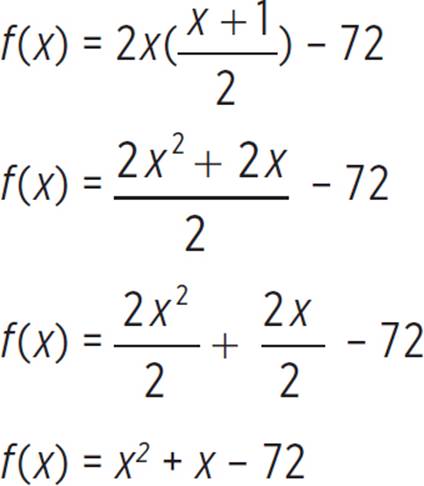
Therefore, a = 1, b = 1, and c = − 72, and we can plug these values into the discriminant.
b2 − 4ac = (1)2 − 4(1)(−72)
= 1 − (−288)
= 1 + 288
= 289

Here, you are asked to find the graph of y = 2(x − 2)2 + 3. Thankfully, the given equation is in the vertex form of a quadratic: y = a(x − h)2 + k. In this form, the vertex of the equation is at point (h, k). Accordingly, the equation has a vertex at (2, 3) and, since a > 0, the parabola will open upwards. Therefore, eliminate (B) for opening downwards, and (C) and (D) for having an incorrect vertex. The only graph that has a vertex at this point is (A).
So the discriminant is positive, indicating that the quadratic has two real solutions.
Next, the question asks you to find the x-intercepts by factoring the quadratic. Recall that when factoring quadratics in the form ax2 + bx + c = (x + m)(x + n), where m and n are factors of ac and m + n = b, if the value of c is negative and the value of b is positive, m and n will have opposite signs, and the larger factor will be positive. Now let’s find the factors of the c value.
|
Factors of c-term (−72) |
Sum of the Factors |
Value of b-term (1) |
|
−1, 72 |
−1 + 72 = 71 |
1 |
|
−2, 36 |
−2 + 36 = 34 |
1 |
|
−3, 24 |
−3 + 24 = 21 |
1 |
|
−4, 18 |
−4 + 18 = 14 |
1 |
|
−6, 12 |
−6 + 12 = 6 |
1 |
|
−8, 9 |
−8 + 9 = 1 |
1 |
There are several factors of 72, but only one set fits the conditions of the quadratic. Therefore, the function f(x) = 2x(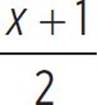 ) − 72 can be factored as f(x) = (x + 9)(x − 8). Now that you’ve factored the quadratic, use the power of the zero product property to solve for x:
) − 72 can be factored as f(x) = (x + 9)(x − 8). Now that you’ve factored the quadratic, use the power of the zero product property to solve for x:
|
(x + 9) |
(x − 8) |
|
x + 9 = 0 |
x − 8 = 0 |
|
x = −9 |
x = 8 |
Therefore, the x-intercepts, or solutions, of the quadratic f(x) = 2x(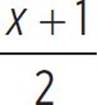 ) − 72 are (8, 0) and (0, −9).
) − 72 are (8, 0) and (0, −9).
Next, you need to find the y-intercept by setting x = 0 and solving for f(x).
f(x) = 2x(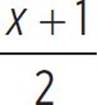 ) − 72
) − 72
f(x) = 2(0)(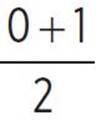 ) − 72
) − 72
f(x) = 0 − 72
f(x) = −72
Thus, the y-intercept of f(x) = 2x(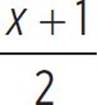 ) − 72 occurs at (0, −72).
) − 72 occurs at (0, −72).
Now that the intercepts are taken care of, find the vertex, (h, k), of the function, given that a = 1, b = 1, and c = −72.
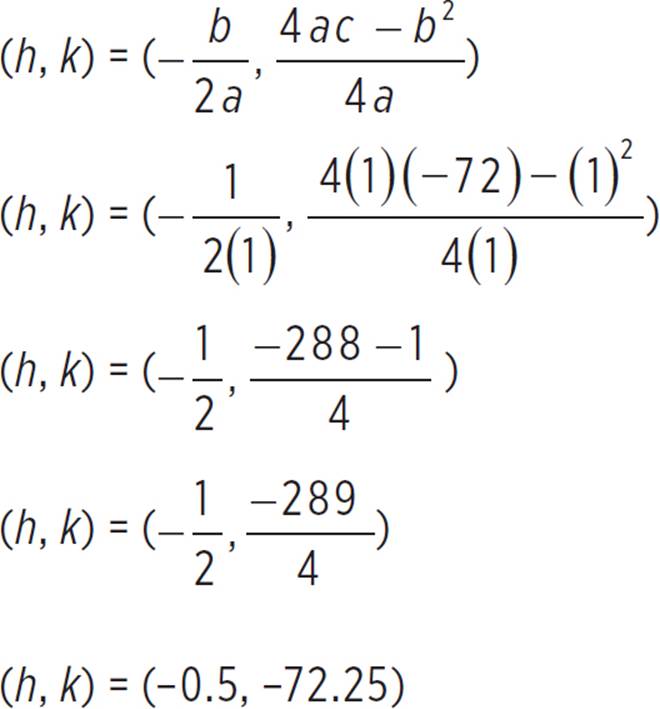
Thus, the vertex of the function is at (−0.5, −72.25) or (−1/2, −289/4).
Next up: Find the axis of symmetry, which is equal to the h-coordinate of the vertex (h, k). Since you’ve already solved for this value, you don’t need to perform the same operation again. Instead, since x = −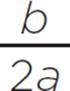 , you can simply state that the axis of symmetry of f(x) = 2x(
, you can simply state that the axis of symmetry of f(x) = 2x(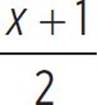 ) − 72 occurs at x = −0.5 or x = −1/2.
) − 72 occurs at x = −0.5 or x = −1/2.
Now determine the minimum or a maximum value of the function, which is also equal to x = −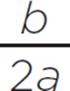 , or the h-coordinate of the vertex (h, k). To determine whether the function has a minimum or a maximum value, look at the value of a. When a > 0, the quadratic will have a minimum value at x = −
, or the h-coordinate of the vertex (h, k). To determine whether the function has a minimum or a maximum value, look at the value of a. When a > 0, the quadratic will have a minimum value at x = −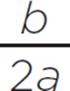 . In this function, the value of a = 1, so the quadratic has a minimum value at x = −0.5 or x = −1/2.
. In this function, the value of a = 1, so the quadratic has a minimum value at x = −0.5 or x = −1/2.
The last part of the question involves graphing the function f(x) = 2x(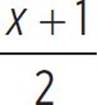 ) − 72 in the coordinate plane, indicating the vertex and the axis of symmetry, shown as a dashed line in the graph on the next page. Once you’ve graphed the function, you can determine the intervals of increase and decrease. Remember, a quadratic function is increasing if the function slopes upward from left to right along the x-axis, and decreasing if the function slopes downward from left to right along the x-axis. Based on the graph on the next page, the function is decreasing from (−∞, −0.5) and increasing from (−0.5, ∞).
) − 72 in the coordinate plane, indicating the vertex and the axis of symmetry, shown as a dashed line in the graph on the next page. Once you’ve graphed the function, you can determine the intervals of increase and decrease. Remember, a quadratic function is increasing if the function slopes upward from left to right along the x-axis, and decreasing if the function slopes downward from left to right along the x-axis. Based on the graph on the next page, the function is decreasing from (−∞, −0.5) and increasing from (−0.5, ∞).
Now put it all together: The function f(x) = 2x(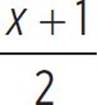 ) − 72 has x-intercepts at (8, 0) and (−9, 0); a y-intercept at (0, −72); a vertex, which is a minimum value, at (−0.5, −72.25); an axis of symmetry at x = −0.5; an interval of decrease from (−∞, −0.5]; and an interval of increase from [−0.5, ∞). Graph all of this as shown below.
) − 72 has x-intercepts at (8, 0) and (−9, 0); a y-intercept at (0, −72); a vertex, which is a minimum value, at (−0.5, −72.25); an axis of symmetry at x = −0.5; an interval of decrease from (−∞, −0.5]; and an interval of increase from [−0.5, ∞). Graph all of this as shown below.
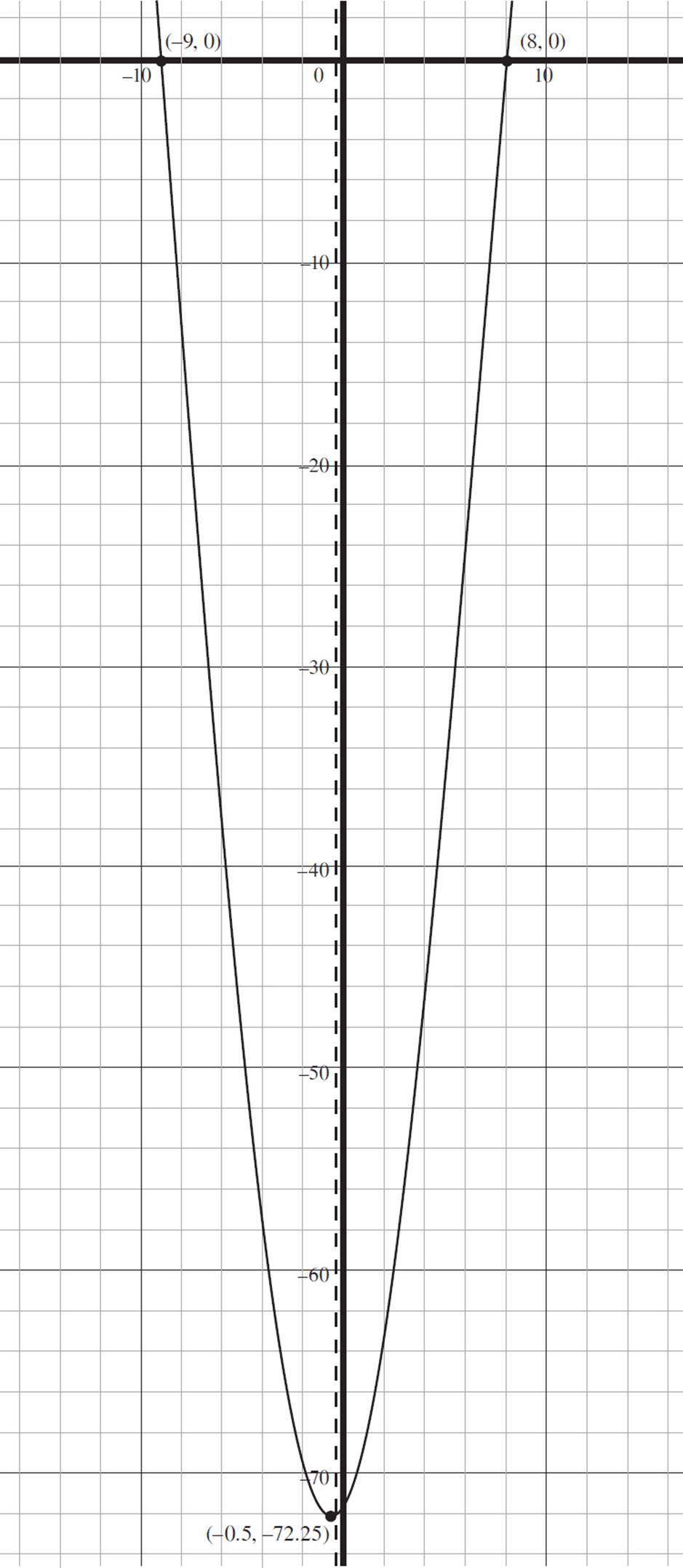
Congratulations! You successfully solved your first major quadratic function question!


By now, you should
be very familiar
with completing the
square—we covered
this in Lessons
3.4 and 6.1!
You may also be asked to solve a quadratic function by completing the square. Let’s refresh our memory about how completing the square works.

Before we move on, let’s try a quadratic function question that involves completing the square.
EXAMPLE 
Find the vertex, axis of symmetry, and roots of f(x) = ![]() (4x2 + 12) + 8x by completing the square. Then, graph the function in the coordinate plane and determine the intervals of increase and decrease, the domain and range, and the end behavior of the function.
(4x2 + 12) + 8x by completing the square. Then, graph the function in the coordinate plane and determine the intervals of increase and decrease, the domain and range, and the end behavior of the function.
Again, this question has multiple parts to it, so tackle each piece in turn. Here we have the function f(x) = ![]() (4x2 + 12) + 8x and need to find the roots, or x-intercepts, by completing the square. In order to do that, however, we first need to expand the quadratic and put it in standard form.
(4x2 + 12) + 8x and need to find the roots, or x-intercepts, by completing the square. In order to do that, however, we first need to expand the quadratic and put it in standard form.
f(x) = ![]() (4x2 + 12) + 8x
(4x2 + 12) + 8x
f(x) = ![]() (4x2) +
(4x2) + ![]() (12) + 8x
(12) + 8x
f(x) = ![]() x2 + 4 + 8x
x2 + 4 + 8x
f(x) = ![]() x2 + 8x + 4
x2 + 8x + 4
Well, that was a messy quadratic! But now that the quadratic expression is in standard form, f(x) = ax2 + bx + c, we know that a = ![]() , b = 8, and c = 4. Next, find the values of d and e to complete the square and factor the quadratic in the form a(x + d)2 + e.
, b = 8, and c = 4. Next, find the values of d and e to complete the square and factor the quadratic in the form a(x + d)2 + e.
Use the values of a, b, and c and the formula given previously to find d as follows:
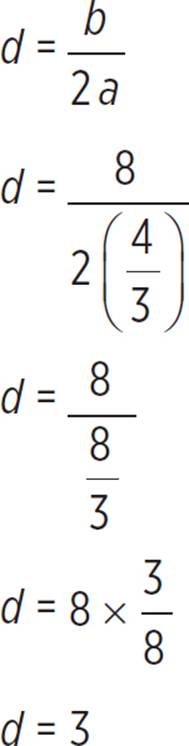
Next, find the value of e, substituting the values of a, b, and c as follows:
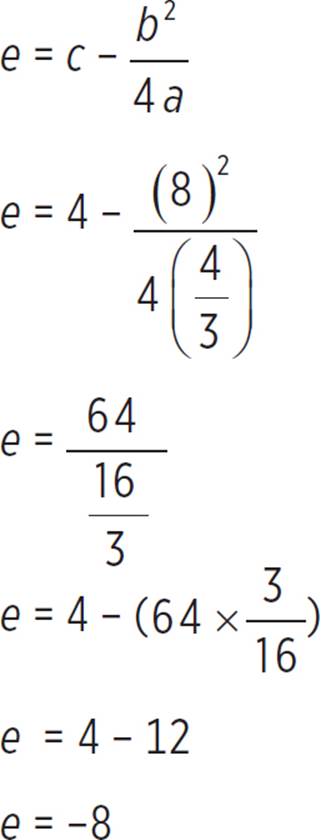
Now that we’ve found d and e, substitute the values a = ![]() , d = 3, and e = −8 into the form associated with completing the square:
, d = 3, and e = −8 into the form associated with completing the square:
a(x + d)2 + e =
![]() (x + 3)2 − 8
(x + 3)2 − 8
Next, set the factored expression equal to zero, simplify the equation, and solve for x:
![]() (x + 3)2 − 8 = 0
(x + 3)2 − 8 = 0
![]() (x + 3)2 = 8
(x + 3)2 = 8
4(x + 3)2 = 24
(x + 3)2 = 6
x + 3 = ±![]()
x = −3 ±![]()
x = − 5.45 and x = −0.55
At last, we’ve found the x-intercepts, or roots, of the quadratic function: (−5.45, 0) and (−0.55, 0). Now find the y-intercept of the function by setting x = 0 and solving for f(x).
f(x) = ![]() (x + 3)2 − 8
(x + 3)2 − 8
f(x) = ![]() (0 + 3)2 − 8
(0 + 3)2 − 8
f(x) = ![]() (9) − 8
(9) − 8
f(x) = 12 − 8
f(x) = 4
Therefore, the y-intercept of f(x) = ![]() (x + 3)2 − 8 occurs at (0, 4).
(x + 3)2 − 8 occurs at (0, 4).
Next, let’s find the vertex, (h, k), of the function, given that a = ![]() , b = 8, and c = 4.
, b = 8, and c = 4.
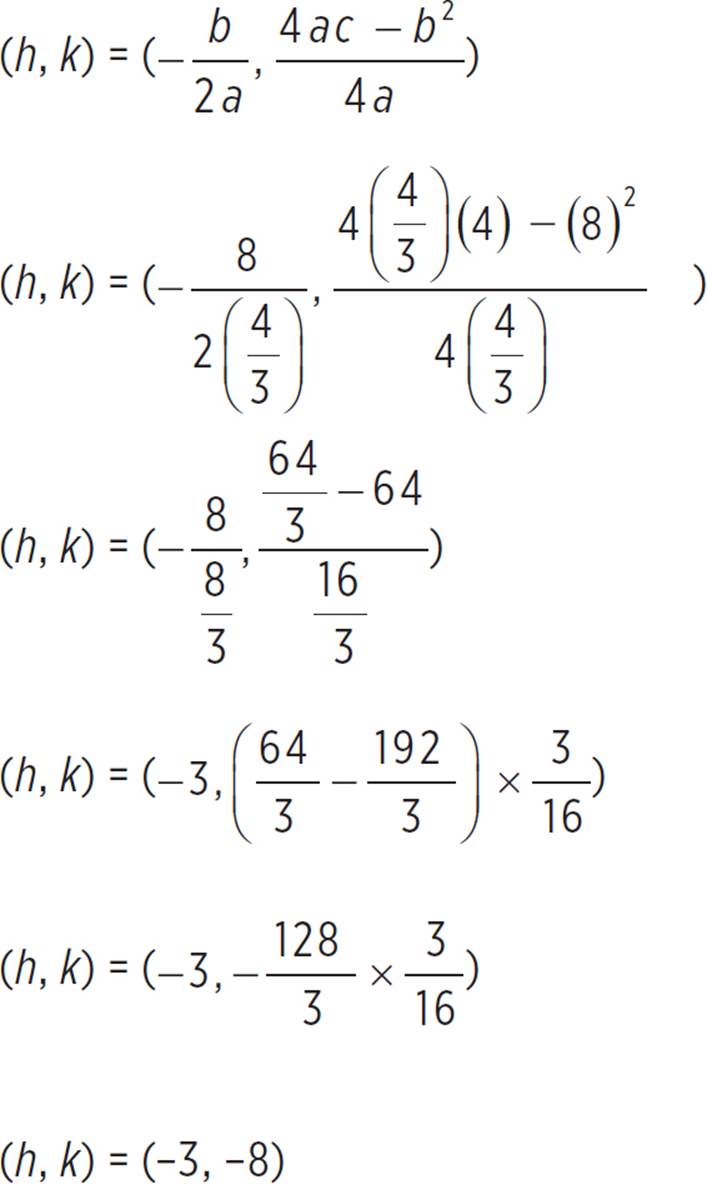
Thus, the vertex is at (−3, −8). Now, we just did a lot of work to find this vertex, but if you’re pressed for time, there’s another way to approach this part of the problem. Take another look at the function f(x) = (4/3)(x + 3)2 − 8. This function is written in vertex form, y = a(x − h)2 + k, and (h, k) is the vertex. So, to find the vertex more quickly, you can just take the values of d and e when the function is in completing the square form. In essence, (d, e) is equivalent to (h, k).
Now let’s find the axis of symmetry, which is equal to the h-coordinate of the vertex (h, k). You have already solved for the value −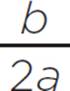 , so you don’t need to perform the same operation again. Rather, you can simply state that the axis of symmetry of f(x) =
, so you don’t need to perform the same operation again. Rather, you can simply state that the axis of symmetry of f(x) = ![]() (x+ 3)2 − 8 occurs at x = −3.
(x+ 3)2 − 8 occurs at x = −3.
At this point, we need to graph the function using the information we’ve found so far. The graph of f(x) = ![]() (x + 3)2 − 8 is below, with the axis of symmetry shown as a dashed line. Once graphed, you can identify the intervals of increase and decrease. Once again, recall that a quadratic function is increasing where the function slopes upwards from left to right along the x-axis and decreasing where the function slopes downwards from left to right along the x-axis. Therefore, based on the graph, the function is decreasing from (−∞, −3] and increasing from [−3, ∞).
(x + 3)2 − 8 is below, with the axis of symmetry shown as a dashed line. Once graphed, you can identify the intervals of increase and decrease. Once again, recall that a quadratic function is increasing where the function slopes upwards from left to right along the x-axis and decreasing where the function slopes downwards from left to right along the x-axis. Therefore, based on the graph, the function is decreasing from (−∞, −3] and increasing from [−3, ∞).
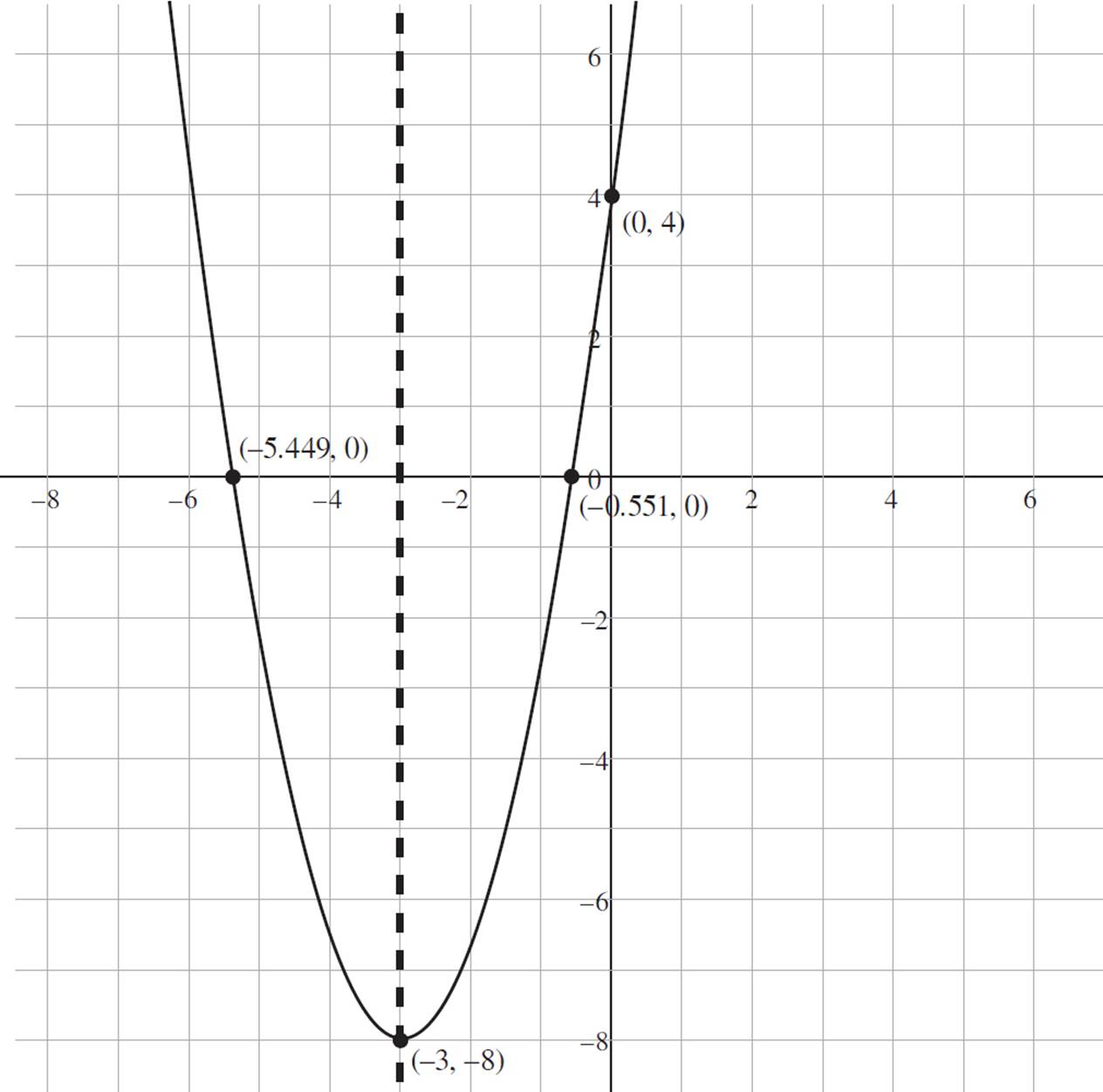
Using the graph, determine the domain and range of the function. You can see that both the left and right ends of the function continue upwards indefinitely. Therefore, the domain of the function is all real numbers, −∞ < x < ∞, which is expressed in interval notation as (−∞, ∞). To find the range, look at the possible y-values for our function. The minimum y-value occurs at y = −3, and the function continues upwards indefinitely. Therefore, the range of our function is all real numbers, −3 ≤ y < ∞, which would be expressed in interval notation as [−3, ∞).
The final part of the question requires you to determine the end behavior of the function. Look at the left end of the function: As the value of x approaches negative infinity, the value of f(x), or y, approaches infinity. Now consider the right end of the function; as the value of x approaches infinity, f(x), or y, also approaches infinity. Therefore, we would express the end behavior as follows:
f(x) → ∞, as x → −∞
f(x) → ∞, as x → ∞

Nice work! Now, it’d be pretty great if every quadratic function you encountered could be handled by factoring or completing the square. Unfortunately, that’s not always the case. Sometimes you’ll need to use the quadratic formula to find the x-intercepts of the function. Let’s practice solving and graphing some quadratic functions that require use of the quadratic formula.
EXAMPLE 
Determine the number of real solutions in the function f(x) = 2x2 − 8x + 6 using the discriminant. If real solutions exist, use the quadratic formula to find the solutions. Then do the following:
a. Identify the y-intercept.
b. Identify the vertex and state whether it is a minimum or maximum.
c. Identify the axis of symmetry.
d. Graph the function in the coordinate plane.
This question is asking for a lot of information, so tackle it one piece at a time. Start by determining if the quadratic has any real solutions by finding the discriminant. Since the function f(x) = 2x2 − 8x + 6 is already in standard form, we know that a = 2, b = −8, and c = 6, and we can plug these values into the discriminant.
b2 − 4ac = (−8)2 − 4(2)(6)
= 64 − 48
= 16
Since the discriminant is positive, the quadratic has two real solutions. Let’s find them! First, find the x- and y-intercepts by using the quadratic formula, since this function is not easily factored.
Now just plug a = 2, b = −8, and c = 6 into the quadratic formula and simplify:
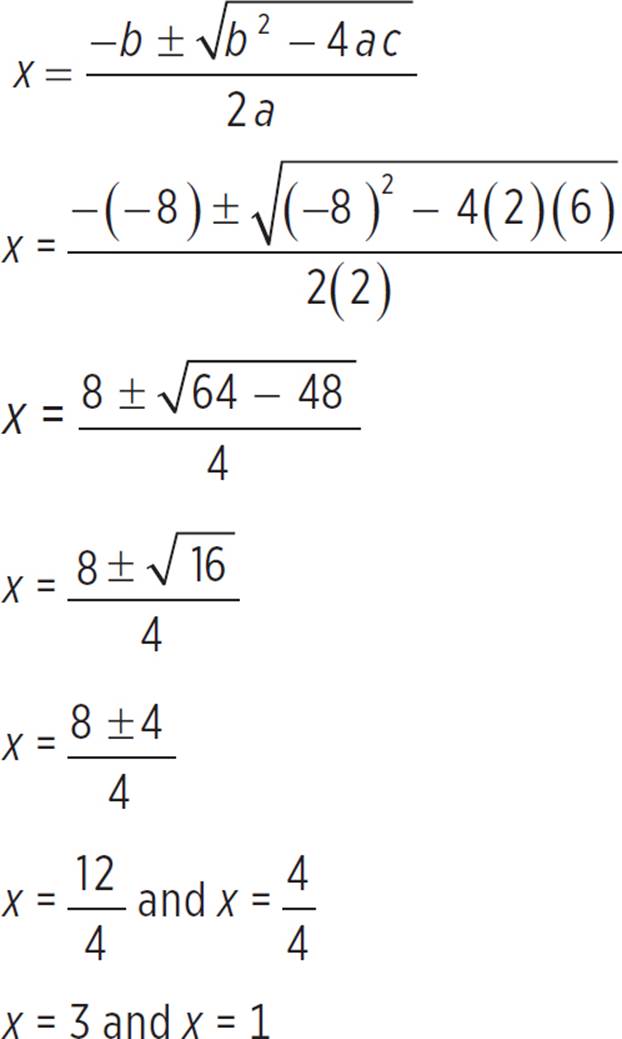
Thus, the x-intercepts of f(x) = 2x2 − 8x + 6 occur at (1, 0) and (3, 0). Now find the y-intercept by setting x = 0 and solving for f(x).
f(x) = 2x2 − 8x + 6
f(x) = 2(0)2 − 8(0) + 6
f(x) = 0 − 0 + 6
f(x) = 6
Therefore, the y-intercept of f(x) = 2x2 − 8x + 6 occurs at (0, 6). Next, we can find the vertex, (h, k), of f(x) = 2x2 − 8x + 6, given that a = 2, b = −8, and c = 6.
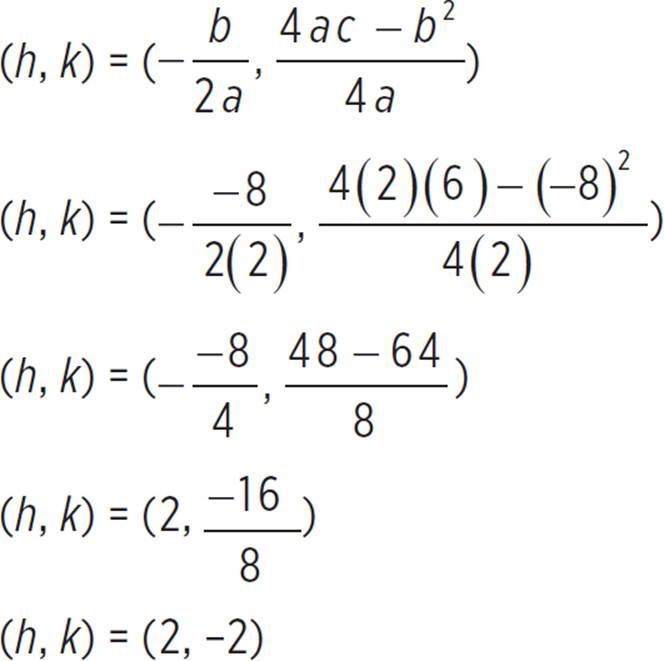
The vertex is thus (2, −2). We can now find the axis of symmetry, which just so happens to be equal to the h-coordinate of the vertex (h, k). But if you forget this, you can always solve for the axis of symmetry:
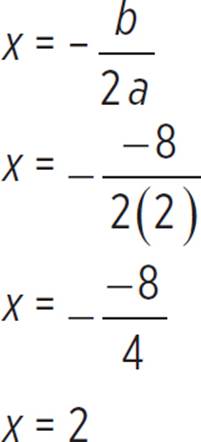
The axis of symmetry for the function f(x) = 2x2 − 8x + 6 occurs at x = 2.
Now determine whether the vertex is a minimum or a maximum value of the function. When a > 0, a quadratic will have a minimum value at x = −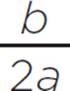 . Since the value of a = 2 in the function f(x) = 2x2 − 8x + 6, the quadratic has a minimum value at x = 2.
. Since the value of a = 2 in the function f(x) = 2x2 − 8x + 6, the quadratic has a minimum value at x = 2.
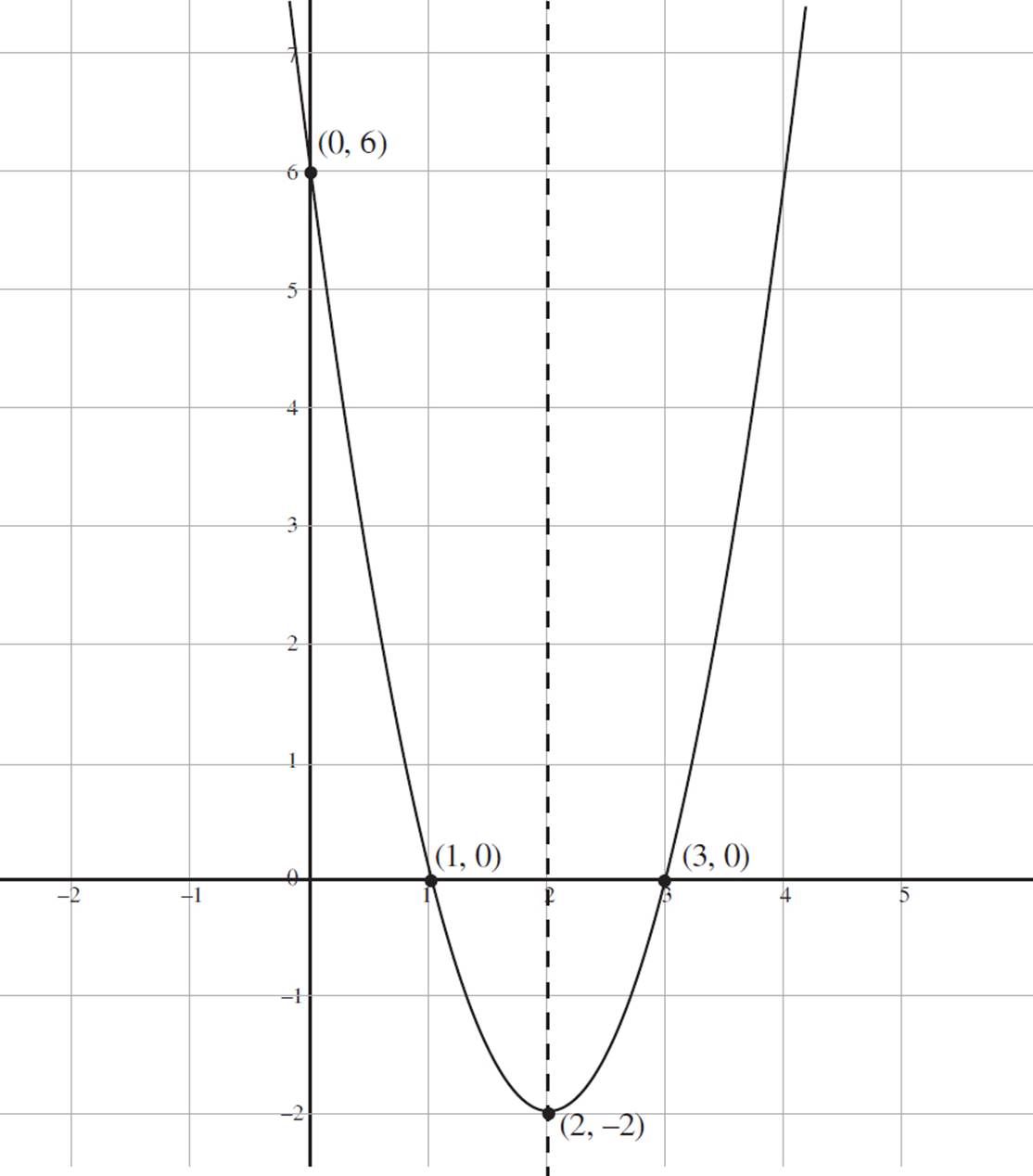
Finally, graph the function f(x) = 2x2 − 8x + 6 in the coordinate plane, indicating the vertex, axis of symmetry, and the minimum value. Put it all together: The function f(x) = 2x2 − 8x + 6 has x-intercepts at (3, 0) and (1, 0); a y-intercept at (0, 6); a vertex, which is also the minimum value, at (2, −2); and the axis of symmetry at x = 2. When you use all of this information to graph the function, the result is the following:
Given the standard
form of an equation
ax2 + bx + c = 0,
the y-intercept
of a parabola
occurs at y = c.

Let’s try one more!
EXAMPLE 
Determine the number of real solutions in the function f(x) = −2x2 + 5x + 4 using the discriminant. If real solutions exist, use the quadratic formula to find the solutions. Then do the following:
a. Identify the y-intercept.
b. Identify the vertex and state whether it is a minimum or maximum.
c. Identify the axis of symmetry.
d. Graph the function in the coordinate plane and determine the domain, range, and end behavior.
Okay, take a deep breath. As always, tackle the individual parts of the question one at a time. Start by determining if the quadratic has any real solutions by finding the value of the discriminant. Since the function f(x) = −2x2 + 5x + 4 is already in standard form, we know that a = −2, b = 5, and c = 4, and we can plug these values in to the discriminant.
b2 − 4ac = (5)2 − 4(−2)(4)
= 25 − (−32)
= 25 + 32
= 57
The discriminant is positive, so the quadratic has two real solutions. Now let’s find them.
Begin by finding the x- and y-intercepts. You can find the x-intercepts of the quadratic by factoring the function or by completing the square, but since this quadratic isn’t very straightforward, use the quadratic formula. Since f(x) = −2x2 + 5x + 4 is in standard form, we know that a = −2, b = 5, and c = 4. Now just plug those values into the quadratic formula and simplify:
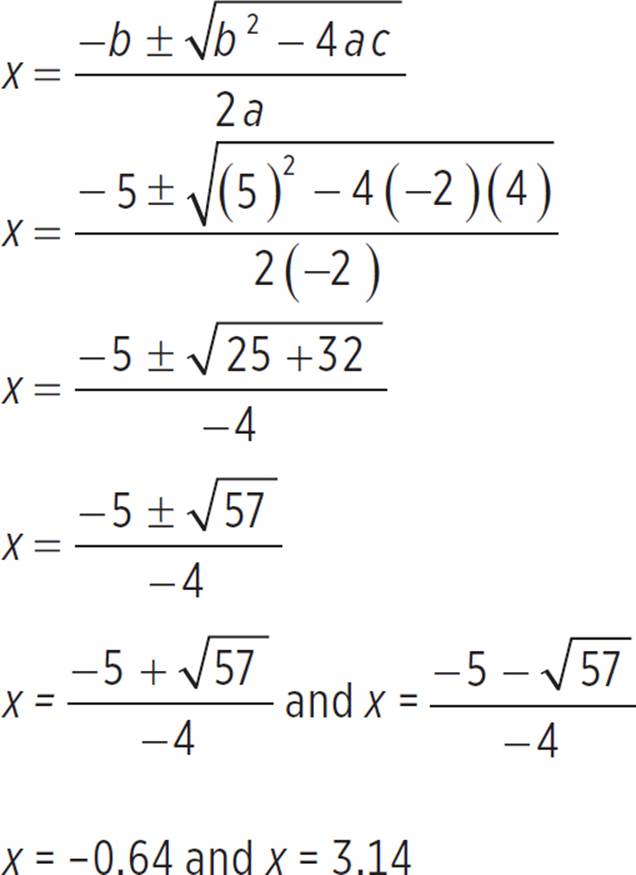
Thus, the x-intercepts of f(x) = −2x2 + 5x + 4 occur at (−0.64, 0) and (3.14, 0). Now find the y-intercept by setting x = 0 and solving for f(x).
f(x) = −2x2 + 5x + 4
f(x) = −2(0)2 − 5(0) + 4
f(x) = 0 − 0 + 4
f(x) = 4
So, the y-intercept of f(x) = −2x2 + 5x + 4 occurs at (0, 4).
Next, find the vertex, (h, k), of f(x) = −2x2 + 5x + 4, given that a = −2, b = 5, and c = 4.
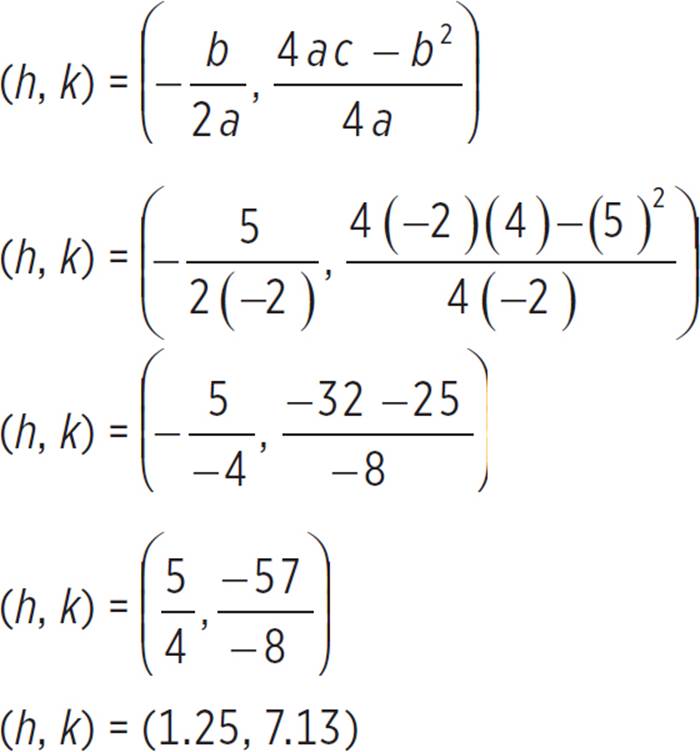
Now that we know the vertex is (1.25, 7.13), we can find the axis of symmetry. Note that the axis of symmetry is equal to the h-coordinate of the vertex (h, k). Alternatively, we could solve for the axis of symmetry:
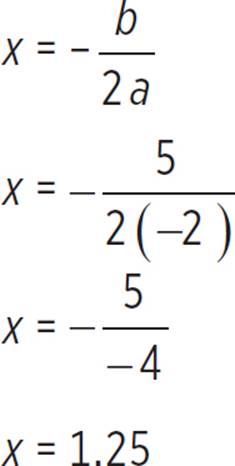
Therefore, the axis of symmetry for the function f(x) = −2x2 + 5x + 4 occurs at x = 1.25.
We can also determine whether the vertex is a minimum or maximum value of the function. Recall that when a < 0, the quadratic will have a maximum value at x = −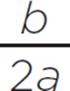 . Since the value of a = −2 in the function f(x) = −2x2 + 5x + 4, the quadratic has a maximum value at x = 1.25.
. Since the value of a = −2 in the function f(x) = −2x2 + 5x + 4, the quadratic has a maximum value at x = 1.25.
Finally, graph the function f(x) = −2x2 + 5x + 4 on the coordinate plane, indicating the vertex, axis of symmetry, shown as a dashed line, and the maximum value.
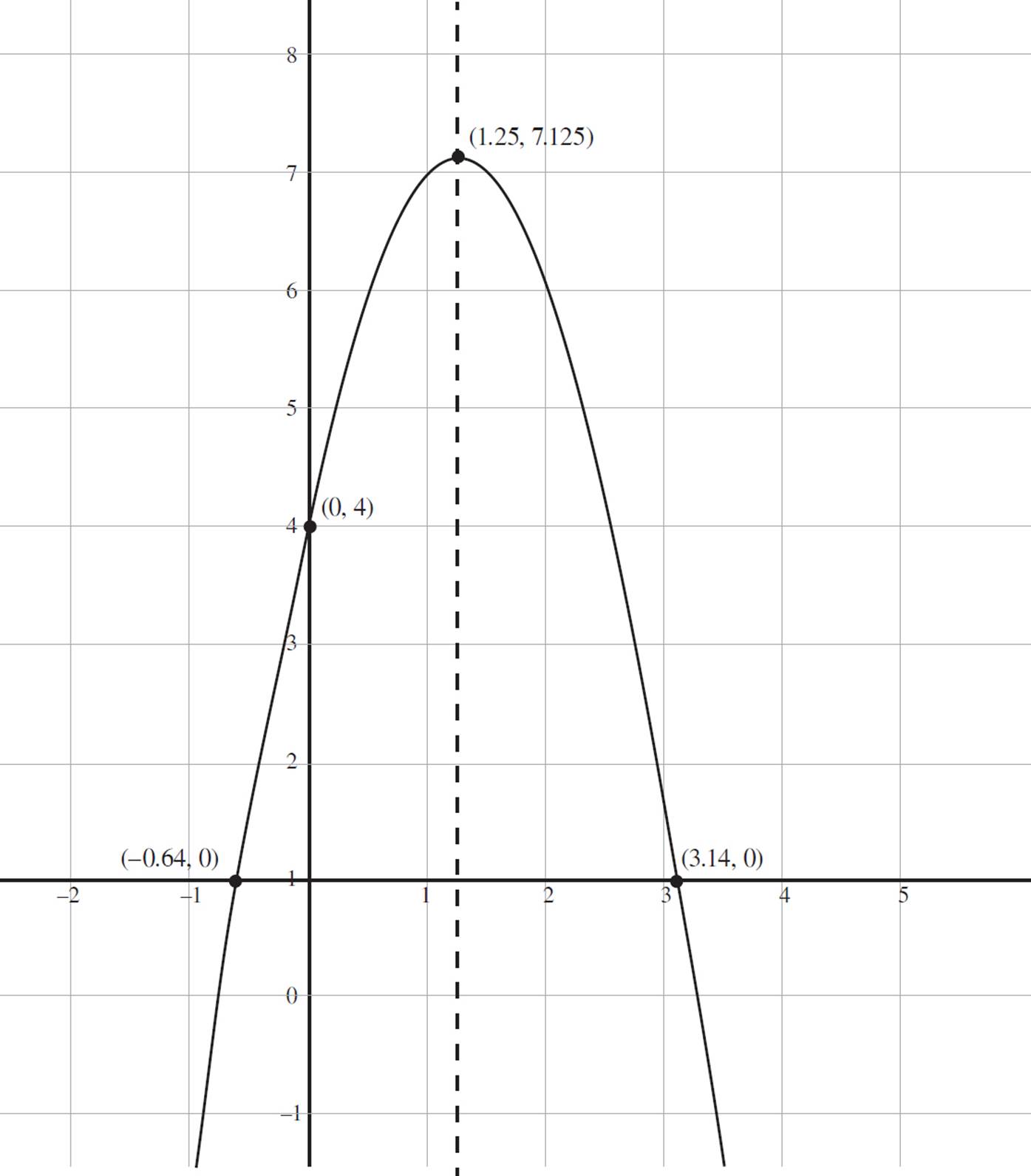
By looking at the graph of f(x) = −2x2 + 5x + 4, we can determine the domain and range of the function. Both the left and right ends of the function continue downward indefinitely, so the domain is all real numbers, −∞ < x < ∞, which is expressed in interval notation as (−∞, ∞).
Now look at the possible y-values for the function. The maximum y-value occurs at 7.125, and the graph continues downwards indefinitely. Therefore, the range of the function is all real numbers, −∞ < y ≤ 7.125, which would be expressed in interval notation as (−∞, 7.125].
Finally, determine the end behavior of f(x) = −2x2 + 5x + 4. Consider the left end the function: As the value of x approaches negative infinity, the value of f(x), or y, also approaches negative infinity. Looking at the right end the function, as the value of xapproaches infinity, f(x), or y, approaches negative infinity. We would express the end behavior like this:
f(x) → −∞, as x → −∞
f(x) → −∞, as x → ∞

Great work! You now know how to tackle all sorts of crazy-looking quadratic functions by factoring, completing the square, and using the quadratic formula. You should also now be able to solve any questions that ask you about the characteristics of a quadratic function. So if your teacher asks you to find the axis of symmetry? No problem! The vertex? Piece of cake! Define the end behavior of a quadratic? You’ve got this! Now test your skills by trying the practice problems on the next page.
DRILL
CHAPTER 8 PRACTICE QUESTIONS
Click here to download a PDF of Chapter 8 Practice Questions.
Directions: Complete the following problems as specified by each question. For extra practice, try using an alternative method to solve the problem or check your work.
1. Which of the following graphs represents the function f(x) = (x + 2)2 + 4 ?
A) 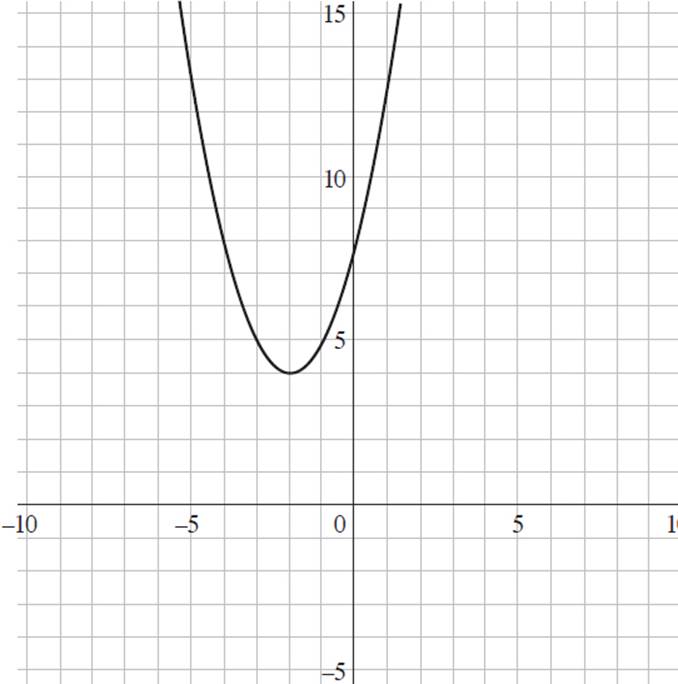
B) 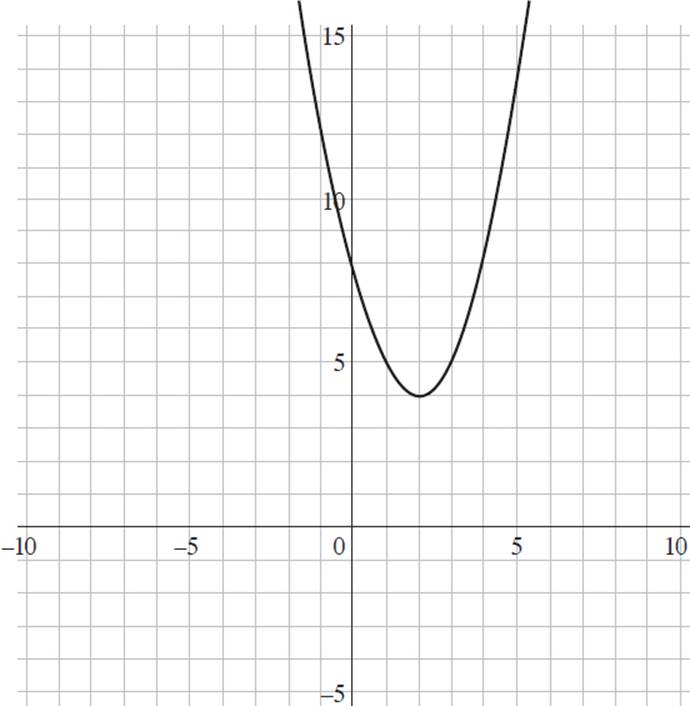
C) 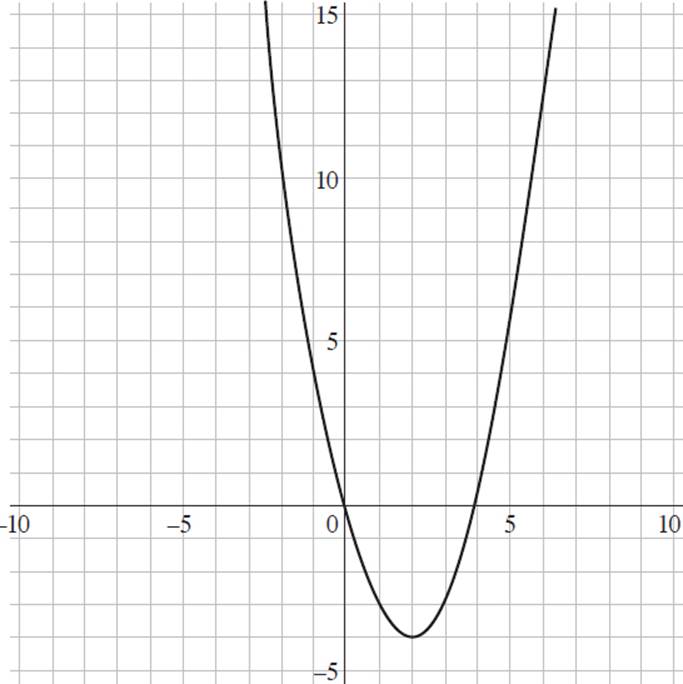
D) 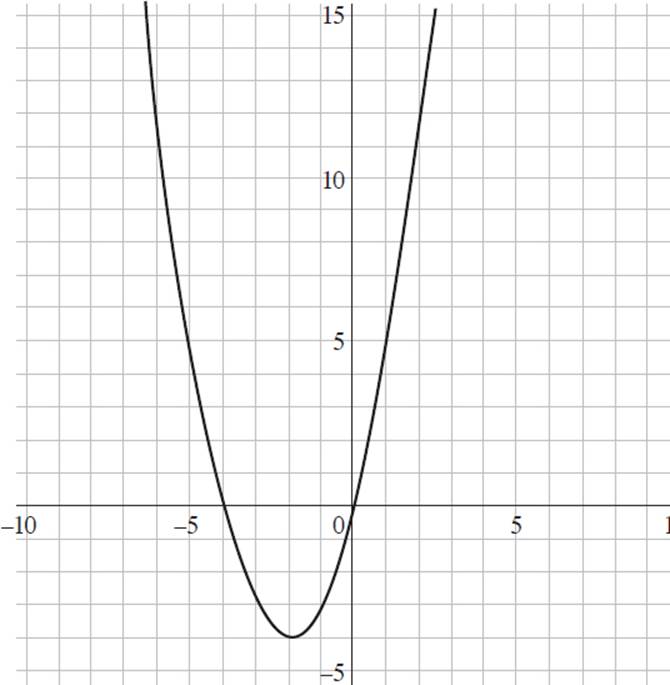
2. Given the function firefly(x) = x2 − 8x + 16:
a. Identify the vertex of the function and state whether it is a minimum or maximum value.
b. Identify the axis of symmetry.
3. Find the solutions of the function go(x) = x2 − 2x − 48 by factoring the quadratic. Then do the following:
a. Find the y-intercept.
b. Find the vertex and state whether it is a minimum or maximum.
c. Graph the function in the coordinate plane.
4. Use the discriminant to determine the number of real solutions in the function stop(x) = 8x2 − 6x + 8. If real solutions exist, use the quadratic formula to do the following:
a. Find the x- and y-intercepts.
b. Identify the vertex and state whether it is a minimum or maximum.
c. Find the axis of symmetry.
5. Use the discriminant to determine the number of real solutions in the function g(x) = (−4x − 3)2 − 2. If real solutions exist, use the quadratic formula to do the following:
a. Find the solutions.
b. Find the y-intercept.
c. Identify the vertex and state whether it is a minimum or maximum.
d. Find the axis of symmetry.
6. Given the graph of ezra(x) = −4x2 + 2x + 6 below, do the following:
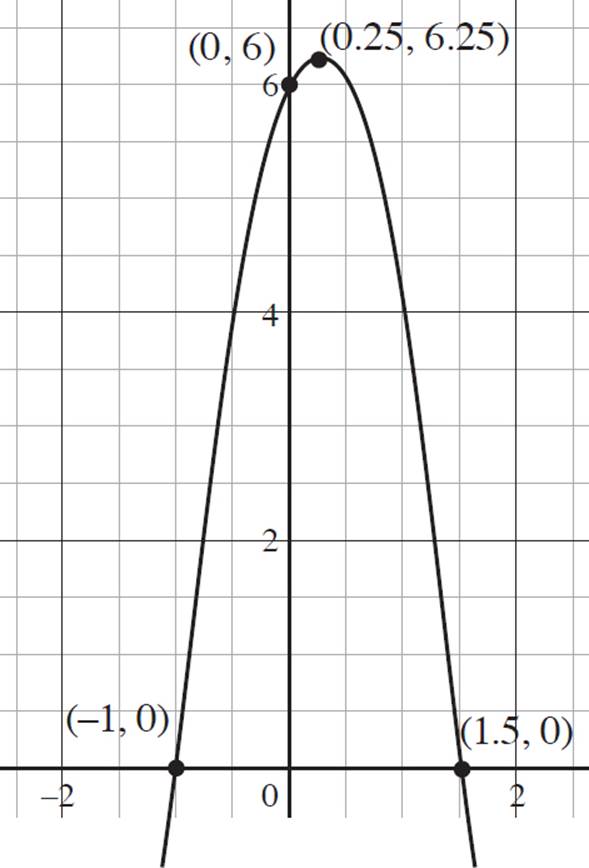
a. Find the intervals of increase and decrease.
b. Identify the domain and range.
c. Determine the end behavior of the function.
7. Find the roots of f(x) = (4x − 3)2 − (12x2 − 2x − 19) by completing the square. Then do the following:
a. Find the y-intercept.
b. Identify the vertex of the function.
c. Graph f(x) in the coordinate plane.
8. Given the function moose(x) = 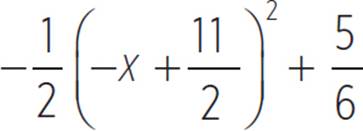 , do the following:
, do the following:
a. Identify the vertex of the function and state whether it is a minimum or maximum.
b. Identify the axis of symmetry.
c. Find the roots of the function.
d. Find the y-intercept.
e. Graph the function.
f. Identify the intervals of increase and decrease.
g. Determine the domain and range of the function.
h. Determine the end behavior of the function.
SOLUTIONS TO CHAPTER 8 PRACTICE QUESTIONS
1. A
This question requires you to determine the graph that represents the function f(x) = (x + 2)2 + 4. Start by finding the y-intercept of the function, as it is the most straightforward to find and will allow you to eliminate some answer choices. To find the y-intercept, set x = 0 and solve for y, or f(x); thus, f(x) = (x + 2)2 + 4, f(x) = (0 + 2)2 + 4, f(x) = 22 + 4, f(x) = 4 + 4, and f(x) = 8. Therefore, the y-intercept of f(x) = (x + 2)2 + 4 is at (0, 8). Eliminate (B) and (D), as they both have y-intercepts at (0, 0).
Now you can select values for x and solve for the associated value of y to see if it appears on either graph. If you plug x = 1 into the function, you will find that f(x) = (x + 2)2 + 4, f(1) = (1 + 2)2 + 4, f(1) = 32 + 4, f(1) = 9 + 4, and f(1) = 13. When you look at (A), the point (1, 13) satisfies the function f(x) = (x + 2)2 + 4. However, in (C), f(1) = 5. Thus, the graph that represents f(x) = (x + 2)2 + 4 is (A).
2. Vertex: (4, 0), minimum; Axis of symmetry: x = 4
Start by finding the vertex of the function, firefly(x) = x2 − 8x + 16. Since the function is already in the standard form of a quadratic, ax2 + bx + c, a = 1, b = −8, and c = 16. You can now plug this information into the formula for the vertex of a quadratic, where (h,k) = 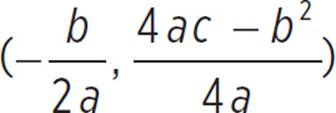 . So, the vertex of the function is (h, k) =
. So, the vertex of the function is (h, k) = 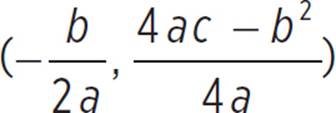 , (h, k) =
, (h, k) = 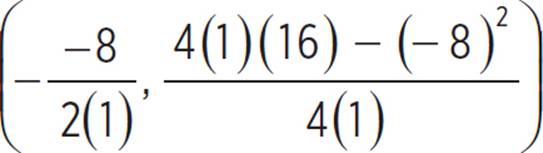 , (h, k) =
, (h, k) = 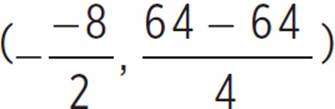 , (h, k) = (4,
, (h, k) = (4, ![]() ), and (h, k) = (4, 0). Therefore, this function has a double root, and the vertex of firefly(x) = x2 − 8x + 16 is (h, k) = (4, 0). Furthermore, given a quadratic function in standard form, f(x) = ax2 + bx + c, the quadratic will have a minimum at x = −
), and (h, k) = (4, 0). Therefore, this function has a double root, and the vertex of firefly(x) = x2 − 8x + 16 is (h, k) = (4, 0). Furthermore, given a quadratic function in standard form, f(x) = ax2 + bx + c, the quadratic will have a minimum at x = −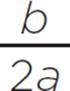 if x > 0 and will have a maximum at x = −
if x > 0 and will have a maximum at x = −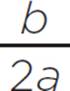 if x < 0. In the quadratic firefly(x) = x2 − 8x + 16, a > 0, so the quadratic has a minimum at (4, 0).
if x < 0. In the quadratic firefly(x) = x2 − 8x + 16, a > 0, so the quadratic has a minimum at (4, 0).
Then find the axis of symmetry, which is equal to x = −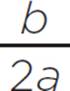 . Since you already found the value of x when you found the h-value of the vertex, you know that the axis of symmetry is x = 4.
. Since you already found the value of x when you found the h-value of the vertex, you know that the axis of symmetry is x = 4.
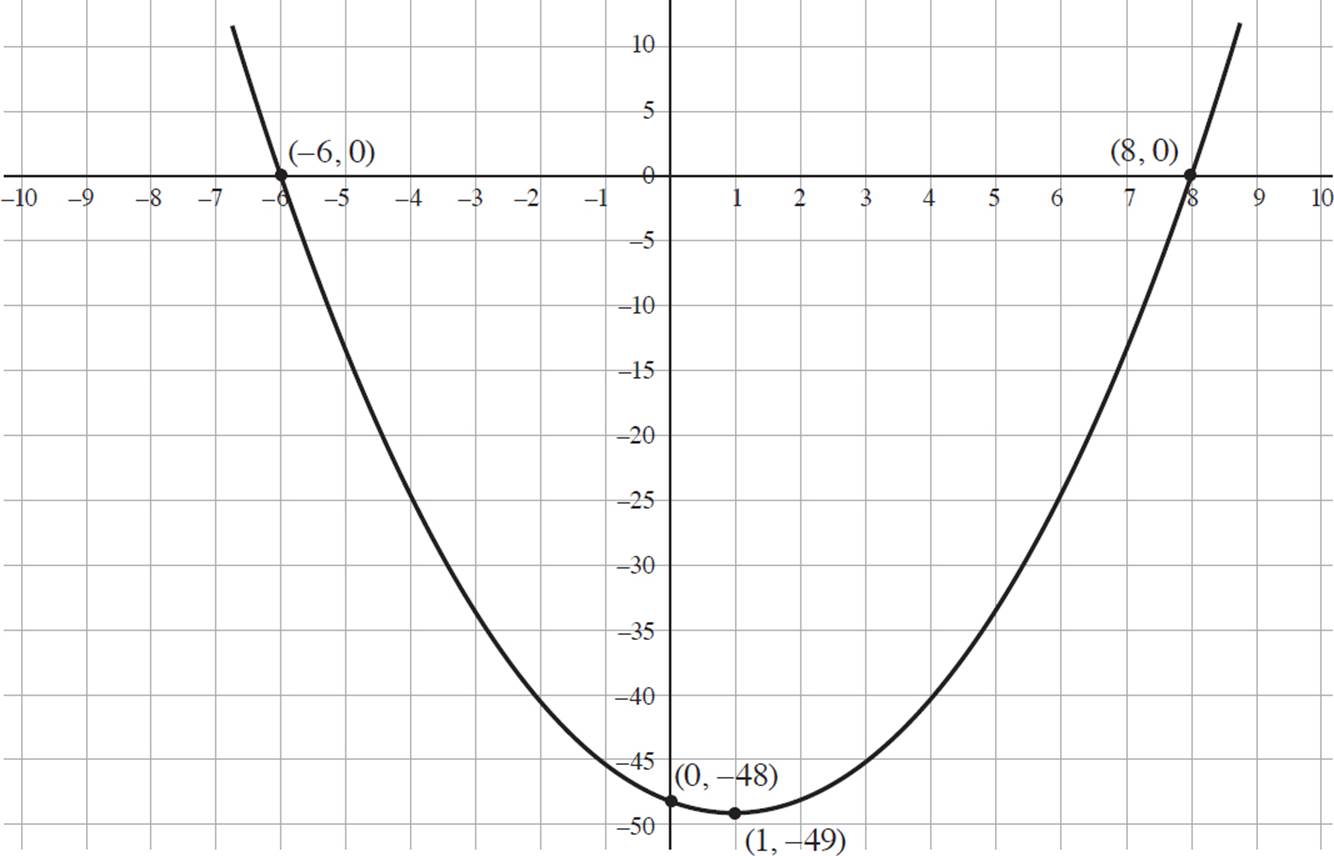
3. Roots: (−6, 0) and (8, 0); y-intercept: (0, −48); Vertex: (1, −49), minimum
This question requires you to factor the function go(x) = x2 − 2x − 48 to find the solutions of the quadratic. Since the quadratic is already in standard form, ax2 + bx + c = 0, you know that, a = 1, b = −2, and c = −48. Based on the rules of factoring, if the b- and c-terms are negative, the factors will have opposite signs, and the larger factor will be negative. Next, find factors of the c-term, −48, that add up to the b-term, −2:
|
Factors of c-term (−48) |
Sum of the Factors |
Value of b-term (−2) |
|
1, −48 |
1 − 48 = −47 |
−2 |
|
2, −24 |
2 − 24 = −22 |
−2 |
|
3, −16 |
3 − 16 = −13 |
−2 |
|
4, −12 |
4 − 12 = −8 |
−2 |
|
6, −8 |
6 − 8 = −2 |
−2 |
In the chart, the only factors of the c-term, −48, that add up to the b-term, −2, are 6 and −8. Thus, you can factor go(x) = x2 − 2x − 48 as (x + 6)(x − 8). Now you can find the values of x by setting each parenthetical term equal to zero and solving for x:
|
(x + 6) |
(x − 8) |
|
x + 6 = 0 |
x − 8 = 0 |
|
x = −6 |
x = 8 |
Therefore, the roots of the quadratic equation occur when x = −6 or x = 8. So, the solutions of the equation are (−6, 0) and (8, 0).
Next, determine the y-intercept of the function by setting x = 0 and solving for y, or go(x): go(x) = x2 − 2x − 48, go(x) = (0)2 − 2(0) − 48, and go(x) = −48. Thus, the y-intercept is (0, −48).
The question then requires that you find the vertex of the quadratic and state whether it is a minimum or maximum value. The vertex of a function is (h, k) = 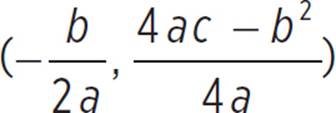 , and since we know that a = 1, b = −2, and c = −48 in go(x) = x2 − 2x − 48, we can find that (h, k) =
, and since we know that a = 1, b = −2, and c = −48 in go(x) = x2 − 2x − 48, we can find that (h, k) = 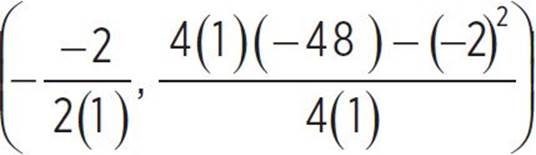 , (h, k) =
, (h, k) = 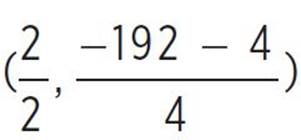 , (h, k) = (1,
, (h, k) = (1, 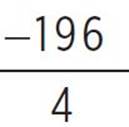 ), and (h, k) = (1, −49). You now need to determine whether the vertex is a minimum or a maximum. Given a quadratic function in standard form, f(x) = ax2 + bx + c, the quadratic will have a minimum at x = −
), and (h, k) = (1, −49). You now need to determine whether the vertex is a minimum or a maximum. Given a quadratic function in standard form, f(x) = ax2 + bx + c, the quadratic will have a minimum at x = −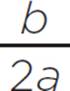 if a > 0, and the quadratic will have a maximum at x = −
if a > 0, and the quadratic will have a maximum at x = −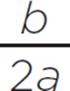 if a < 0. In the quadratic go(x) = x2 − 2x − 48, a > 0, so the quadratic has a minimum at (1, −49).
if a < 0. In the quadratic go(x) = x2 − 2x − 48, a > 0, so the quadratic has a minimum at (1, −49).
Finally, use the information you’ve gleaned to plot the graph in the coordinate plane.
4. No real solutions
Once again, you need to find a lot of information about the function stop(x) = 8x2 − 6x + 8. Start by using the discriminant, b2 − 4ac, to determine the number of real solutions in the function. Since the function is already in the standard form of a quadratic, ax2 +bx + c, you know that a = 8, b = −6, and c = 8. Thus, the discriminant is b2 − 4ac, (−6)2 − 4(8)(8), and 36 − 256 = −220. Because the discriminant in negative, the quadratic has no real solutions.
5. Two real solutions: x = 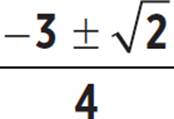 ; y-intercept: (0, 7); vertex: (−3/4, −2), minimum; axis of symmetry: x = −3/4
; y-intercept: (0, 7); vertex: (−3/4, −2), minimum; axis of symmetry: x = −3/4
For this question, you need to find a lot of information about the function g(x) = (−4x − 3)2 − 2. Start by using the discriminant, b2 − 4ac, to determine the number of real solutions in the function. In order to use the discriminant, however, you must first rewrite the function in the standard form of a quadratic, ax2 + bx + c: g(x) = (−4x − 3)2 − 2, g(x) = (−4x − 3)(−4x − 3) − 2, g(x) = 16x2 + 12x + 12x + 9 − 2, and g(x) = 16x2 + 24x + 7. Therefore, a = 16, b = 24, and c = 7. The discriminant is b2 − 4ac, (24)2 − 4(16)(7), and 576 − 448 = 128. Because the discriminant is positive, the quadratic has two real solutions.
Now, use the quadratic formula to find those real solutions using the values a = 16, b = 24, and c = 7; thus, x = 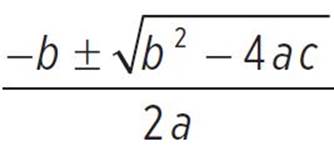 , x =
, x = 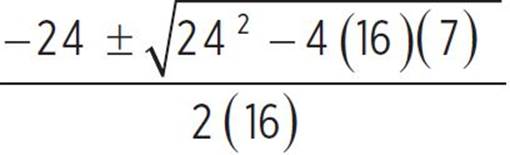 , x =
, x = 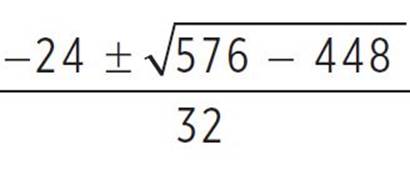 , x =
, x = 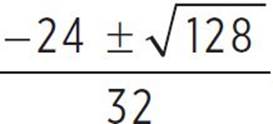 , x =
, x = 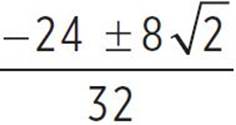 , and x =
, and x = 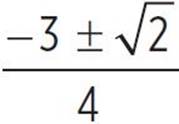 .
.
Next, the question asks you to find the y-intercept, so set x = 0 and find the value of y, or g(x): g(x) = 16x2 + 24x + 7, g(x) = 16(0)2 + 24(0) + 7, g(x) = 0 + 0 + 7, and g(x) = 7. Thus, the y-intercept occurs at (0, 7).
Now find the vertex of the function and determine whether it is the minimum or maximum of the function. The vertex of a function is (h, k) = 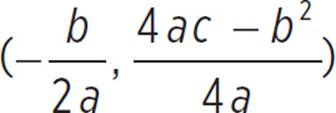 , and since we know that a = 16, b = 24, and c = 7 in g(x), we can find that (h, k) =
, and since we know that a = 16, b = 24, and c = 7 in g(x), we can find that (h, k) = 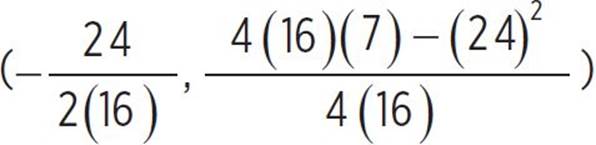 , (h, k) =
, (h, k) = 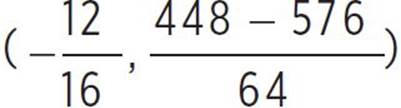 , (h, k) = (
, (h, k) = (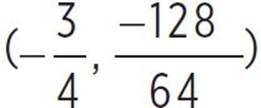 ), and (h, k) = (−
), and (h, k) = (−![]() , −2).
, −2).
Next, determine whether the vertex is a minimum or a maximum. Given a quadratic function in standard form, f(x) = ax2 + bx + c, the quadratic will have a minimum at x = −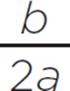 if a > 0, and the quadratic will have a maximum at x = −
if a > 0, and the quadratic will have a maximum at x = −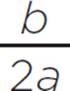 if a < 0. In the quadraticg(x) = 16x2 + 24x + 7, a > 0, so the quadratic has a minimum at (−3/4, −2). Finally, let’s find the axis of symmetry, which is equal to x = −
if a < 0. In the quadraticg(x) = 16x2 + 24x + 7, a > 0, so the quadratic has a minimum at (−3/4, −2). Finally, let’s find the axis of symmetry, which is equal to x = −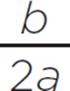 . Since you already found the value of when you found the h-value of the vertex, you know that the axis of symmetry is found at x = −3/4.
. Since you already found the value of when you found the h-value of the vertex, you know that the axis of symmetry is found at x = −3/4.
6. Interval of increase: (−∞, 0.25); Interval of decrease (0.25, ∞); Domain: (−∞, ∞); Range: (−∞, 6.25]; End f(x) → −∞, as x → −∞ and f(x) → −∞, as x → ∞
This question provides the graph of ezra(x) = −4x2 + 2x + 6 and asks you to determine the intervals of increase and decrease, domain and range, and end behavior of the function. The vertex of ezra(x) does not lie on an integer-based point; you need to find the vertex of the function so that you can accurately state the intervals of increase and decrease. Since ezra(x) is already in standard form, where ax2 + bx + c, you know that a = −4, b = 2, and c = 6. Now you can find the vertex of the function, which is (h, k) = 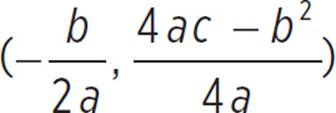 . Thus, (h, k) =
. Thus, (h, k) = 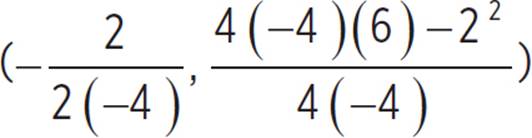 , (h, k) = (
, (h, k) = (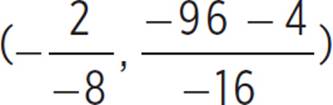 ), (h, k) =
), (h, k) = 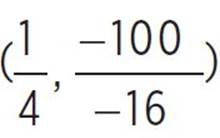 , and (h, k) =
, and (h, k) = 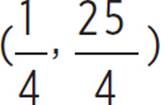 or (0.25, 6.25). Now that you know the vertex of the function, you can determine the intervals of increase and decrease. Recall that a quadratic function is increasing if the function slopes upwards from left to right along the x-axis, and a quadratic function is decreasing if the function slopes downwards from left to right along the x-axis. Therefore, the function ezra(x) is increasing from (−∞, 0.25) and decreasing from (0.25, ∞).
or (0.25, 6.25). Now that you know the vertex of the function, you can determine the intervals of increase and decrease. Recall that a quadratic function is increasing if the function slopes upwards from left to right along the x-axis, and a quadratic function is decreasing if the function slopes downwards from left to right along the x-axis. Therefore, the function ezra(x) is increasing from (−∞, 0.25) and decreasing from (0.25, ∞).
Next, determine the domain and range of the function. Looking at the graph of ezra(x) = −4x2 + 2x + 6, you can see that both the left and right ends of the function continue downward indefinitely. Therefore, the domain of the function is all real numbers, −∞ < x < ∞, which is expressed in interval notation as (−∞, ∞). Now look at the possible y-values for the function to determine the range. The maximum y-value occurs at 6.25, and the graph continues downwards indefinitely. Therefore, the range of the function is all real numbers, −∞ < y < 6.25, which is expressed in interval notation as (−∞, 6.25].
Finally, you need to determine the end behavior of the function. Consider the left end the function, ezra(x) = −4x2 + 2x + 6. Here, as the value of x approaches negative infinity, the value of f(x), or y, also approaches negative infinity. Next, consider the right end of the function; as the value of x approaches infinity, f(x), or y, approaches negative infinity. Thus, you would express the end behavior as f(x) → −∞, as x → −∞ and f(x) → −∞, as x → ∞.
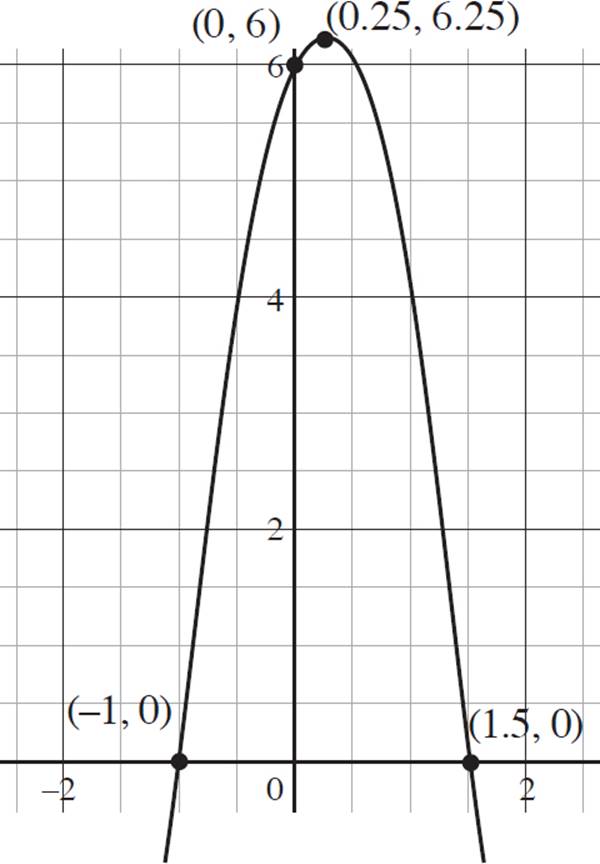
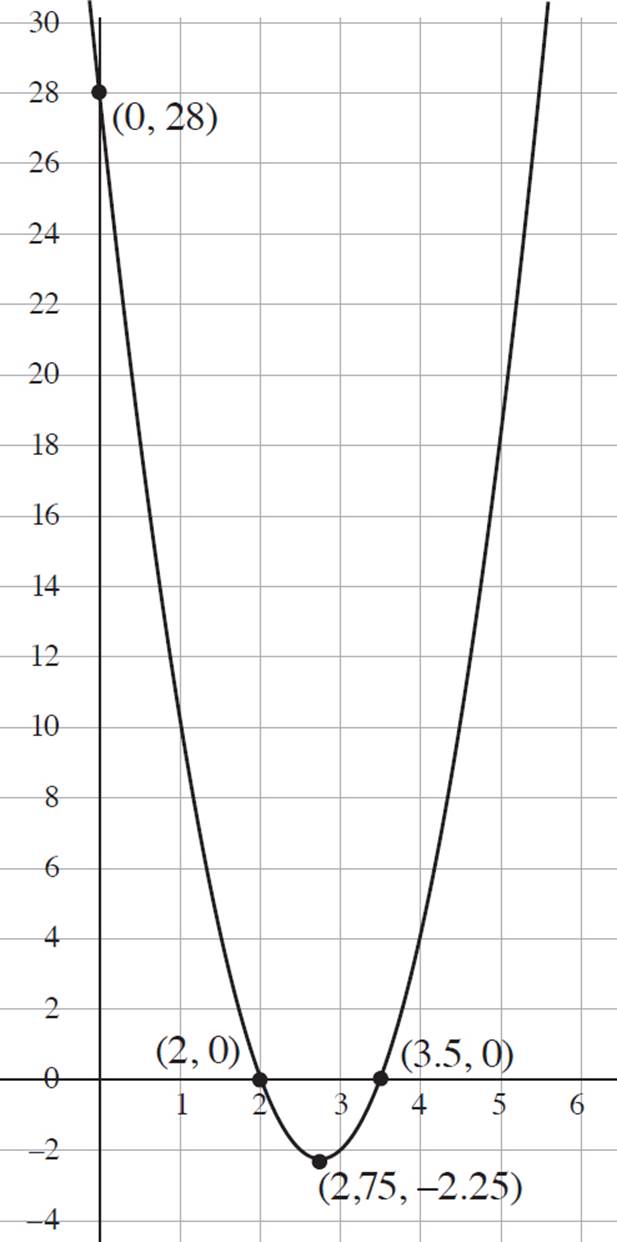
7. Roots: (2, 0) and (3.5, 0); y-intercept: (0, 28); Vertex: (2.75, −2.25)
Begin by expanding the quadratic and putting it in standard form, where ax2 + bx + c: f(x) = (4x − 3)2 − (12x2 − 2x − 19), f(x) = (4x − 3)(4x − 3) − 12x2 + 2x + 19, f(x) = 16x2 − 12x − 12x + 9 − 12x2 + 2x + 19, and f(x) = 4x2 − 22x + 28. Therefore, a = 4, b = −22, and c = 28.
Now find the values of d, where d = 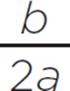 , and e, where e = c −
, and e, where e = c − 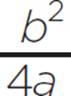 , to complete the square and factor the quadratic in the form a(x + d)2 + e. Use the values of a, b, and c and the formula given previously to find d: d =
, to complete the square and factor the quadratic in the form a(x + d)2 + e. Use the values of a, b, and c and the formula given previously to find d: d = 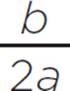 , d =
, d = 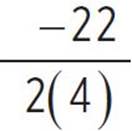 , d =
, d = 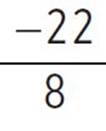 , and d = −2.75. Next, find the value of e, substituting the values of a, b, and c: e = c −
, and d = −2.75. Next, find the value of e, substituting the values of a, b, and c: e = c − 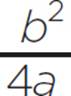 , e = 28 −
, e = 28 − 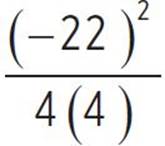 , e = 28 −
, e = 28 − 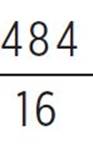 , e = 28 − 30.25, and e = −2.25. Now that you’ve found d and e, substitute the values a = 4, d = −2.75, and e = −2.25 into the form associated with completing the square: a(x + d)2 + e = 4(x − 2.75)2 − 2.25.
, e = 28 − 30.25, and e = −2.25. Now that you’ve found d and e, substitute the values a = 4, d = −2.75, and e = −2.25 into the form associated with completing the square: a(x + d)2 + e = 4(x − 2.75)2 − 2.25.
Next, set the factored expression equal to zero, simplify the equation, and solve for x: 4(x − 2.75)2 − 2.25 = 0, 4(x − 2.75)2 = 2.25, (x − 2.75)2 = 0.5625, (x − 2.75) = ±![]() , x = 2.75 ± 0.75, and x = 2 and x = 3.5. Therefore, the x-intercepts, or roots, of the quadratic function are (2, 0) and (3.5, 0).
, x = 2.75 ± 0.75, and x = 2 and x = 3.5. Therefore, the x-intercepts, or roots, of the quadratic function are (2, 0) and (3.5, 0).
To find the y-intercept of the function, set x = 0 in the standard form of the function f(x), f(x) = 4x2 − 22x + 28; here, f(x) = 4x2 − 22x + 28, f(x) = 4(0)2 − 22(0) + 28, and f(x) = 28. Thus, the y-intercept of the function occurs at (0, 28).
Next, find the vertex, (h, k), of the function, given that a = 4, b = −22, and c = 28; (h, k) = 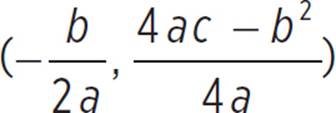 , (h, k) =
, (h, k) = 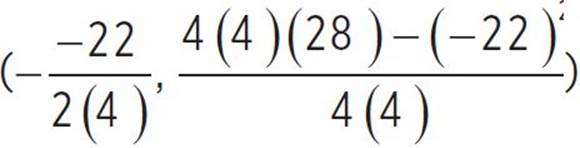 , (h, k) =
, (h, k) = 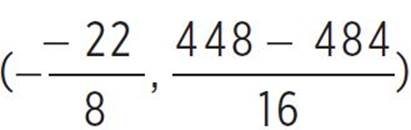 , (h, k) = (2.75,
, (h, k) = (2.75, 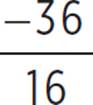 ), and (h, k) = (2.75, −2.25).
), and (h, k) = (2.75, −2.25).
Finally, use the information you’ve gleaned to plot the graph in the coordinate plane. Refer to the graph below.
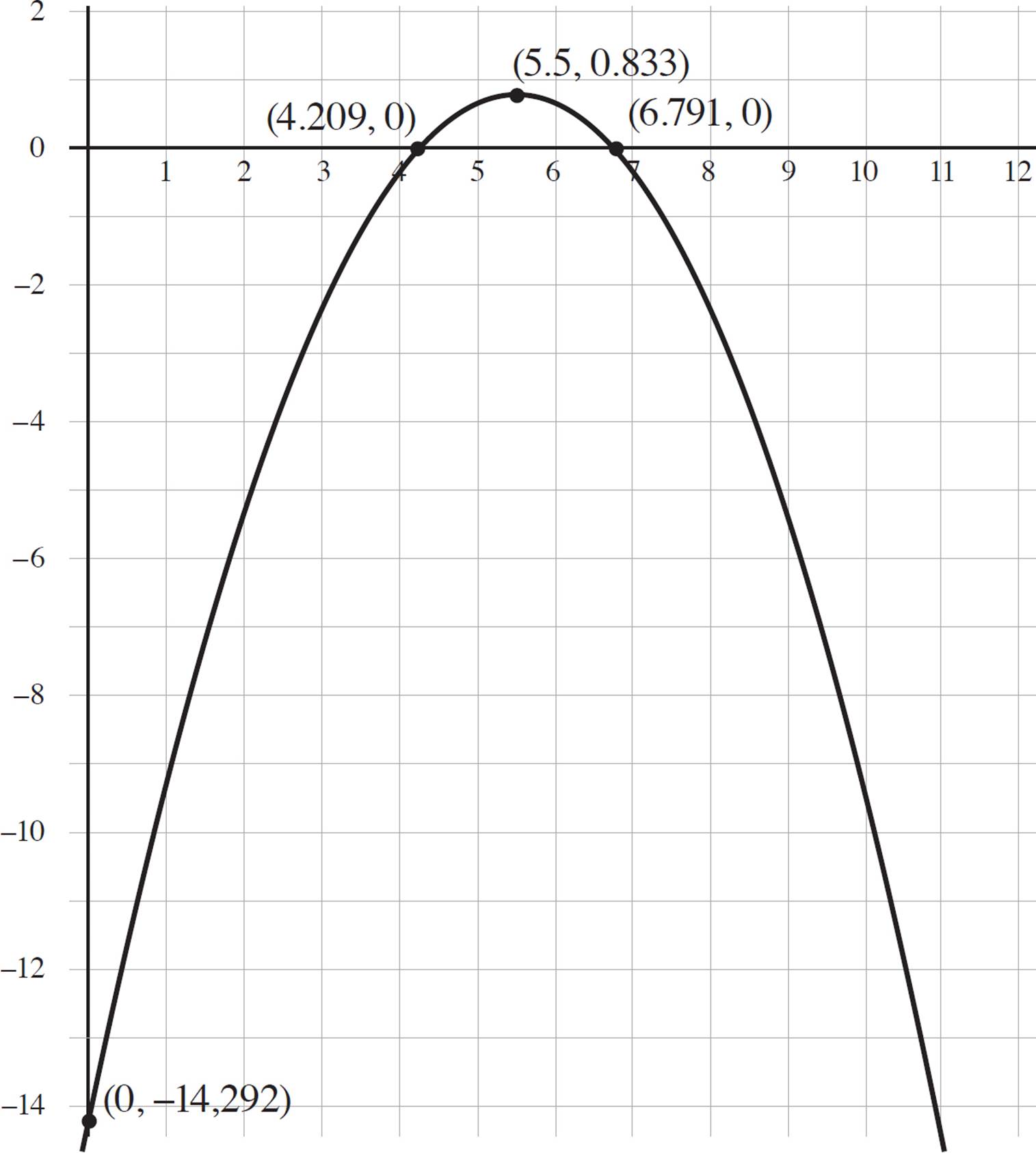
8. Roots: 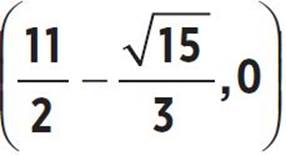 and
and 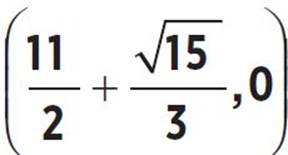 , or (4.21, 0) and (6.791, 0); y-intercept: (0, −
, or (4.21, 0) and (6.791, 0); y-intercept: (0, − ) or (0, −14.29); Vertex:
) or (0, −14.29); Vertex: 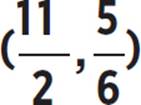 or (5.5, 0.833), maximum; Axis of symmetry: x =
or (5.5, 0.833), maximum; Axis of symmetry: x = ![]() or x = 5.5; Interval of increase: (−∞, 5.5]; Interval of decrease [5.5, ∞); Domain: (−∞, ∞); Range: (−∞, 0.833]; End f(x) → −∞, as x → −∞ and f(x) → −∞, as x → ∞
or x = 5.5; Interval of increase: (−∞, 5.5]; Interval of decrease [5.5, ∞); Domain: (−∞, ∞); Range: (−∞, 0.833]; End f(x) → −∞, as x → −∞ and f(x) → −∞, as x → ∞
You’re given the function moose(x) = 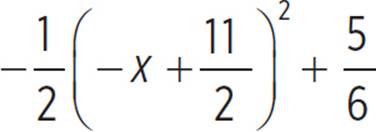 , and asked to identify the vertex of the function, stating whether the vertex is a minimum or maximum value, and identify the axis of symmetry. Note that there is a direct connection between the completing the square form of a quadratic, where a(x + d)2 + e, and the vertex form of a quadratic, where a(x − h )2 + k and (h, k) is the vertex. Thus, the function moose(x) =
, and asked to identify the vertex of the function, stating whether the vertex is a minimum or maximum value, and identify the axis of symmetry. Note that there is a direct connection between the completing the square form of a quadratic, where a(x + d)2 + e, and the vertex form of a quadratic, where a(x − h )2 + k and (h, k) is the vertex. Thus, the function moose(x) = 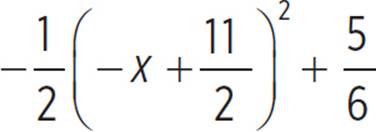 can be written in vertex form as moose(x) =
can be written in vertex form as moose(x) = 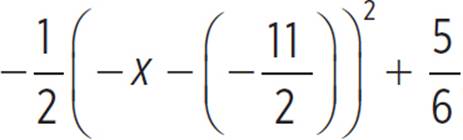 , where the vertex of the function is at
, where the vertex of the function is at  , as −x −
, as −x − 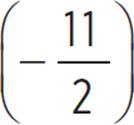 = 0 and x =
= 0 and x = ![]() .
.
Next, determine whether the vertex is a minimum or a maximum. Given a quadratic function in standard form, f(x) = ax2 + bx + c, the quadratic will have a minimum if a > 0, and the quadratic will have a maximum at if a < 0. In the quadratic moose(x) = 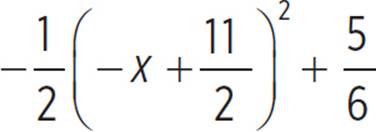 , a < 0, so the quadratic has a maximum at
, a < 0, so the quadratic has a maximum at  . You can now find the axis of symmetry, which is equal to the x-coordinate of the vertex; thus, the axis of symmetry is found at x =
. You can now find the axis of symmetry, which is equal to the x-coordinate of the vertex; thus, the axis of symmetry is found at x = ![]() or x = 5.5.
or x = 5.5.
Now find the roots of the function and the y-intercept. Start by finding the roots of the function: 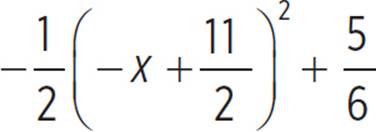 = 0,
= 0, 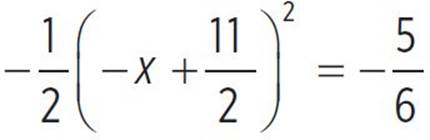 ,
, 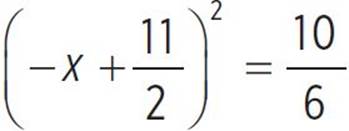 , −x +
, −x + 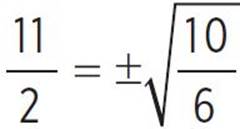 , −x +
, −x + 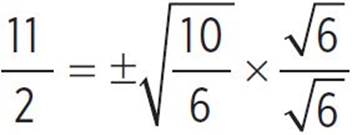 , −x +
, −x + 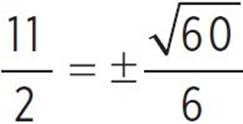 , −x +
, −x + 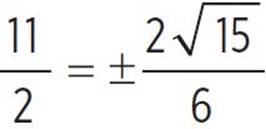 , −x +
, −x + 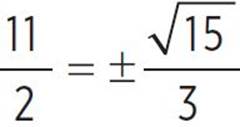 , x +
, x + 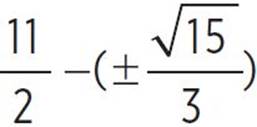 ,x =
,x = 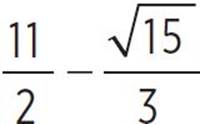 and
and 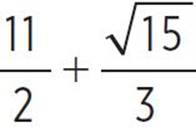 or x = 4.209 and x = 6.791. Therefore, the roots of the function occur at
or x = 4.209 and x = 6.791. Therefore, the roots of the function occur at 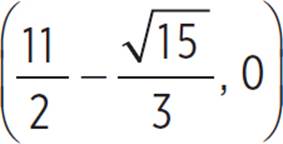 and
and 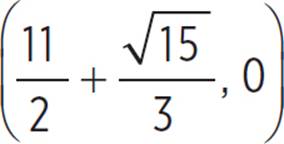 or (4.209, 0) and (6.791, 0).
or (4.209, 0) and (6.791, 0).
In order to find the y-intercept of the function, set x = 0 and solve for moose(x): moose(x) = 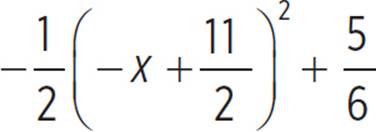 , moose(x) =
, moose(x) = 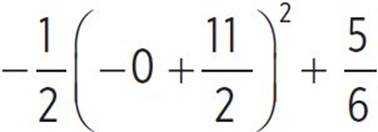 , moose(x) =
, moose(x) = 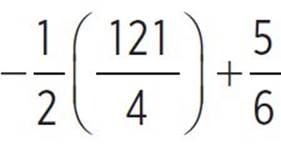 , moose(x) =
, moose(x) = 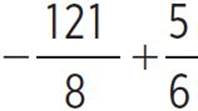 , moose(x) =
, moose(x) = 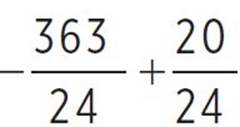 , and moose(x) = −
, and moose(x) = − or −14.292. Thus, the y-intercept occurs at (0, −
or −14.292. Thus, the y-intercept occurs at (0, − ) or (0, −14.292).
) or (0, −14.292).
At this point, you can use the information you’ve found to graph moose(x) in the coordinate plane, as shown on the next page. Once the function is graphed, you can determine the intervals of increase and decrease, domain and range, and end behavior of the function. A quadratic function is increasing if the function slopes upwards from left to right along the x-axis, and decreasing if the function slopes downwards from left to right along the x-axis. In the function moose(x), the function is increasing from −∞ to the vertex, (5.5, 0.833) and decreasing from the vertex to −∞. Thus, the function moose(x) is increasing from (−∞, 5.5] and decreasing from [5.5, ∞).
Now determine the domain and range of the function. Based on the graph of moose(x), both the left and right ends of the function continue downward indefinitely. Therefore, the domain is all real numbers, −∞ < x < ∞, which is expressed in interval notation as (−∞, ∞). Next, look at the possible y-values to determine the range. The maximum y-value occurs at (5.5, 0.833), and the graph continues downwards indefinitely. Thus, the range of the function is all real numbers, −∞ < y < 0.833, which is expressed in interval notation as (−∞, 0.833].
Finally, determine the end behavior of 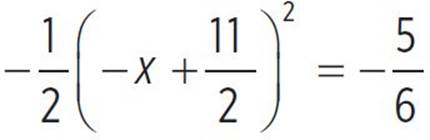 . Consider the left end the function,
. Consider the left end the function, 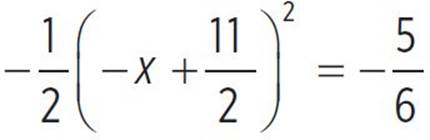 ; here, as the value of x approaches negative infinity, the value of f(x), or y, also approaches negative infinity. Now consider the right end of the function; here, as the value of x approaches infinity, f(x), or y, approaches negative infinity. Therefore, you would express the end behavior as f(x) → −∞, as x → −∞ and f(x) → −∞, as x → ∞.
; here, as the value of x approaches negative infinity, the value of f(x), or y, also approaches negative infinity. Now consider the right end of the function; here, as the value of x approaches infinity, f(x), or y, approaches negative infinity. Therefore, you would express the end behavior as f(x) → −∞, as x → −∞ and f(x) → −∞, as x → ∞.
REFLECT
Congratulations on completing Chapter 8!
Here’s what we just covered.
Rate your confidence in your ability to:
•Explain the key features of quadratic functions
1 2 3 4 5
•Determine the solutions to a quadratic function by factoring, completing the square, or using the quadratic formula
1 2 3 4 5
•Use the discriminant to determine whether a quadratic function has real or complex solutions
1 2 3 4 5
•Find the intercepts, minimum and maximum, and axis of symmetry of a quadratic function
1 2 3 4 5
•Find the domain and range, intervals of increase and decrease, and end behavior of a quadratic function
1 2 3 4 5
•Graph quadratic functions
1 2 3 4 5
If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.
CHAPTER 8 KEY POINTS
![]() The standard form of a quadratic function is f(x) = ax2 + bx + c = 0, where x is the variable and a, b, and c, are constants, and a ≠ 0.
The standard form of a quadratic function is f(x) = ax2 + bx + c = 0, where x is the variable and a, b, and c, are constants, and a ≠ 0.
![]() A quadratic function is quadratic expression set equal to f(x), or y, and is the algebraic representation of the path of a parabola, or the symmetrical curve created by a quadratic.
A quadratic function is quadratic expression set equal to f(x), or y, and is the algebraic representation of the path of a parabola, or the symmetrical curve created by a quadratic.
![]() The discriminant is b2 − 4ac.
The discriminant is b2 − 4ac.
○ If the discriminant is positive, the quadratic equation will have two real solutions.
○ If the discriminant is zero, the quadratic equation will have one real solution.
○ If the discriminant is negative, the quadratic equation will have two complex solutions, or solutions that include the imaginary number i.
![]() The quadratic formula is x
The quadratic formula is x 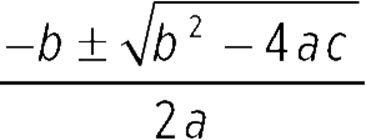 .
.
![]() The vertex (h, k) for any quadratic ax2 + bx + c can be determined with (h, k) = (
The vertex (h, k) for any quadratic ax2 + bx + c can be determined with (h, k) = (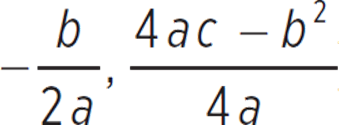 ).
).
![]() The vertex form of a quadratic is given by y = a(x − h)2 + k, where (h, k) is the vertex.
The vertex form of a quadratic is given by y = a(x − h)2 + k, where (h, k) is the vertex.
○ If the value of a is positive, the graphed quadratic will resemble a smile.
○ If the value of a is negative, the quadratic will resemble a frown.
![]() The axis of symmetry for any quadratic ax2 + bx + c can be determined with x = −
The axis of symmetry for any quadratic ax2 + bx + c can be determined with x = −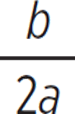 .
.
![]() The minimum or maximum value of a quadratic function occurs at x = −
The minimum or maximum value of a quadratic function occurs at x = −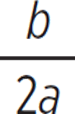 .
.
○ If the value of a > 0, the function has a minimum value.
○ If the value of a < 0, the function has a maximum value.
![]() The domain of a function is all possible x-values for which the function exists, while the range of a function is all possible y-values for which the function exists.
The domain of a function is all possible x-values for which the function exists, while the range of a function is all possible y-values for which the function exists.
![]() A quadratic function is increasing if the function slopes upwards from left to right along the x-axis.
A quadratic function is increasing if the function slopes upwards from left to right along the x-axis.
![]() A quadratic function is decreasing if the function slopes downwards from left to right along the x-axis.
A quadratic function is decreasing if the function slopes downwards from left to right along the x-axis.
![]() The end behavior of a function is the behavior of f(x) as x approaches either positive or negative infinity.
The end behavior of a function is the behavior of f(x) as x approaches either positive or negative infinity.