High School Algebra II Unlocked (2016)

Lesson 2.3. Variation Equations

REVIEW

DISTANCE FORMULA: distance = rate × time

A variation equation can be written as a variable set equal to a single term in which a constant is multiplied and/or divided by one or more other variables.

In a direct variation, two variables are directly proportional; one is a constant multiple of the other. A direct variation is of the form a = kb, where a and b are variables and k is some constant, known as the constant of variation. Another way to view a direct variation is in the form a/b = k, meaning that the two variables have a constant ratio. If one variable increases, the other variable must increase proportionally (by the same factor).

In a direct variation a = kb,
we say, “a varies directly
as b.” In more common,
everyday language, we say,
“a varies directly with b.”

In an inverse variation, one variable is inversely proportional to the other variable. The product of the two variables is constant, so ab = k, or a = k/b, where a and b are variables and k is the constant of variation. If one variable increases, the other variable must decrease by the same factor, so that the product is still the constant, k.

In a joint variation, a variable varies directly with more than one other variable. A joint variation in three variables is in the form a = kbc, where a, b, and c are variables and k is the constant of variation. Here, a varies directly as the product of b and c. If the value of b or c is held constant, then a varies directly as the other variable.

In a combined variation, a variable both varies directly with one or more variables and varies inversely with one or more other variables. The simplest form of a combined variation is a = k • b/c (which can also be written as a = kb/c), where a, b, and c are variables and k is the constant of variation. Here a varies directly as b and varies inversely as c, when the other variable is held constant.

Describe the variation relationship and the value of k for each of the volume equations below.

V_{rectangular prism} = lwh

V_pyramid = 1/3 Bh

V_cylinder = πr²h

For a rectangular prism, volume varies jointly as l, w, and h (length, width, and height), and k = 1.

For a pyramid, volume varies jointly as B (the area of its base) and h (height), and k = 1/3.

For a cylinder, volume varies directly as h, when r is held constant, so k = πr² in that case. We cannot say that the volume varies jointly as r and h, because r is squared. The relationship between V and r is not directly proportional when h is held constant. (If rdoubles, V quadruples, not doubles.)

To solve algebraically, substitute −2x + 3 for y in the second equation. After setting the entire thing equal to 0, by adding, subtracting, and dividing from both sides, you should be able to factor the quadratic to find that the x-values of 1 and 4 are solutions. These can then be substituted into each equation to solve for their corresponding y-values, which yields (1, 1) and (4, −5).

Alternatively, you could graph both given equations, as shown below, and look for the points of intersection. The correct answer in either method is (C).

You can use variation relationships to set up equations and solve problems.

At 4:00 P.M., Jorge and Martin started driving toward one another on the same highway, each at a constant speed. They passed one another when Jorge had driven 80 miles and Martin had driven 96 miles. Write an equation that relates Jorge’s speed to Martin’s speed. If they passed one another at 5:20 P.M., at what speeds were they each driving?

For this situation, we can use the relationship distance = rate × time, or d = rt, and rewrite it as t = d/r. Let’s call Jorge’s rate j and Martin’s rate m. For Jorge, t = 80/j, and for Martin, t = 96/m. Time is inversely proportional to speed. Since Jorge and Martin drove the same period of time until passing one another, t has the same value in both equations. We can substitute to get 80/j = 96/m. Cross-multiply to get 80m = 96j. If we solve for j, we get j = 80/96 m, or j = 5/6 m simplified. This direct variation equation relates Jorge’s speed to Martin’s speed.

If they passed one another at 5:20 P.M., then they each drove for 1 hour and 20 minutes, or 1 1/3 hours. We can say t = 4/3, where t is in hours. Substitute this into Martin’s t = 96/m equation to get 4/3 = 96/m. The solution is m = 72, so Martin’s driving speed was 72 miles per hour.

The units must match,
so we must express time
in hours to match speed
in miles per hour.

Jorge’s speed in relation to Martin’s speed is given by j = 5/6 m, so j = 5/6 (72) = 60. Jorge was driving at a speed of 60 miles per hour. We could also have used the equation t = 80/j with t = 4/3 to solve for j, also resulting in j = 60.

The d = rt relationship is a very simple one, but certain complicated relationships can still be understood in terms of variation relationships.

Caitlin plans to take out a business loan, the size of which will be determined by what monthly payment amount she can afford for a five-year repayment of the loan. She has found a bank that will give her a loan of any amount between $5,000 and $50,000 at a 3.6% interest rate compounded annually. To find the amount, P, of her monthly payment due, she uses the formula P = 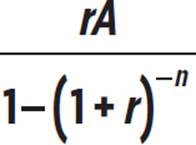, where A represents the amount of the loan, r represents the interest rate per month (as a decimal), and n represents the total number of monthly payments. What is the relationship between the loan amount and the monthly payment amount? Write and graph an equation representing this relationship. Use the graph to determine what loan amount Caitlin should apply for, if she can put $450 per month toward its repayment.

Here is how you may see combined variations on the ACT.

The number of minutes it takes a group of waiters at a certain catering company to set up for a dinner event varies directly with the square root of the number of guests and inversely with the number of waiters working the event. If c represents the constant of variation, which of the following expressions represents the number of minutes it will take w waiters to set up for a dinner event with n guests?

A. cw

B.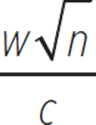

C.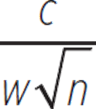

D.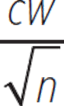

E.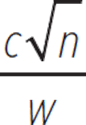

Even though the formula P = 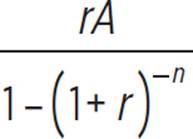looks messy, the values of r and n are constant for this particular situation. So, P varies directly as A, with a constant of variation of .

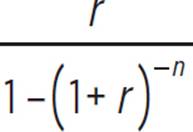The 3.6% interest rate is an annual interest rate, compounded annually, so r, the interest rate per month, is 0.036/12, or 0.003. The variable n represents the total number of monthly payments in the five years in which Caitlin plans to repay the loan, so n = 5 ⋅ 12 = 60. Let’s substitute the values of r and n into the formula.

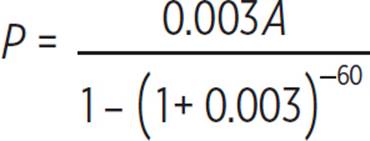
Rounding the coefficient off to the nearest thousandth, this simplifies to P = 0.018A. The graph of P = 0.018A for 5000 ≤ A ≤ 50,000 is shown on the following page.

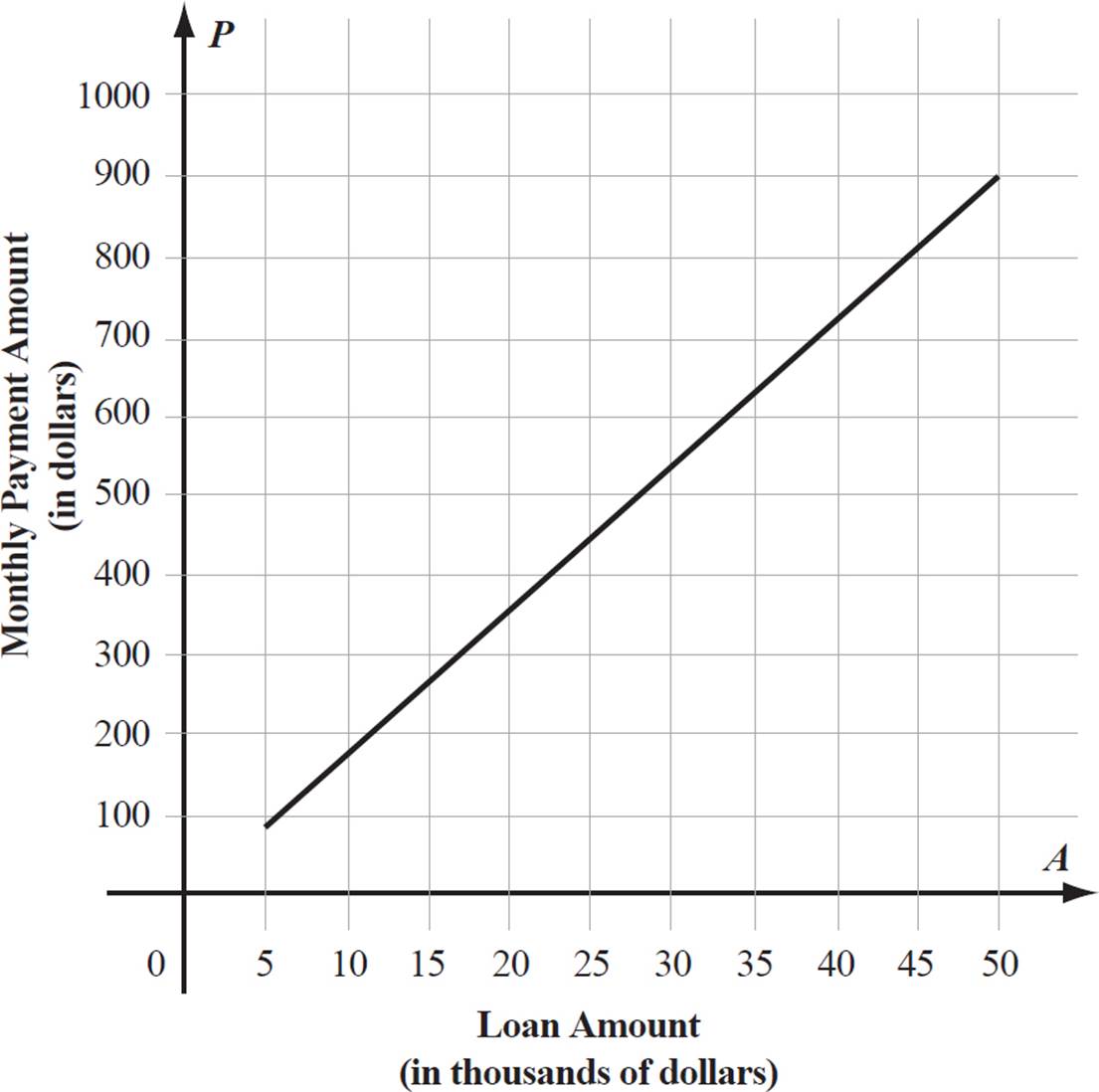
The monthly payment amount is on the vertical axis, so find the point on the line segment that aligns with 450 on the vertical axis. The A-value, or loan amount, of this point is 25, but this is in thousands of dollars. So, if Caitlin can pay $450 per month toward the loan repayment, she should take out a $25,000 loan.

To confirm our answer, let’s substitute 25,000 for A in P = 0.018A.

P = 0.018(25,000) = 450

Yes, a $25,000 loan at the terms described results in a $450 monthly payment amount.