High School Algebra II Unlocked (2016)
Chapter 3. Radical and Rational Equations and Inequalities
Lesson 3.4. Radical Equations in One Variable
REVIEW
An inverse operation undoes what the original operation did. Addition and subtraction are inverse operations, and multiplication and division are inverse operations. Taking the square root is the inverse operation of squaring, and taking the cube root is the inverse operation of cubing.
A radical equation is an equation that contains a radical expression. The radicals you will encounter most often are square roots, but radicals also include cube roots and roots of other degrees.
To solve a radical equation, isolate the radical on one side of the equation and use the inverse operation. For example, for a square root, square both sides, and for a cube root, cube both sides. Just watch out for extraneous solutions when raising to an even power!
How does squaring
both sides produce
extraneous solutions?
Look at a numerical
example. The equation
−3 = 3 is false, but
when you square both
sides, you get the true
equation 9 = 9. When
we find solutions to
a squared equation,
they may not actually
make the original
radical equation true.

Solve the following equation for x.
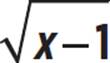 + 3 = x
+ 3 = x
First, subtract 3 from both sides, to isolate the radical expression.
|
|
|
|
x − 1 = (x − 3)2 |
Square both sides of the equation. |
|
x − 1 = x2 − 6x + 9 |
Expand the squared binomial. |
|
0 = x2 − 7x + 10 |
Move all terms to one side of the equation. |
|
0 = (x − 5)(x − 2) |
Factor the quadratic. |
|
x = 5 or x = 2 |
Solve for each factor set equal to 0. |
Test each of these values in the original equation. We cannot use any other equation from later in the solution process, because the act of squaring is what produces extraneous solutions, and squaring both sides was one of the first things we did.
|
|
|
|
|
|
|
2 + 3 ≟ 5 |
1 + 3 ≟ 2 |
|
5 = 5 |
4 ≠ 2 |
The equation 5 = 5 is true, so x = 5 is a solution. The equation 4 = 2 is not true, so x = 2 is an extraneous solution. The only solution to the equation 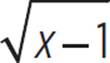 + 3 = x is x = 5.
+ 3 = x is x = 5.


Find all possible solutions for a.
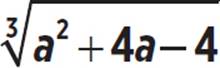 − a = 0
− a = 0
Add a to both sides to isolate the cube root on one side of the equation.
|
|
|
|
a2 + 4a − 4 = a3 |
Cube both sides. |
|
0 = a3 − a2 − 4a + 4 |
Move all terms to one side of the equation. |
|
0 = a2(a − 1) − 4(a − 1) |
Factor out the common factor from each pair of terms. |
|
0 = (a − 1)(a2 − 4) |
Use the distributive property to rewrite as two factors. |
|
0 = (a − 1)(a + 2)(a − 2) |
Factor the difference of squares. |

If you didn’t see the
trick of factoring the
cubic into two pairs
of (a − 1) multiplied
by some common
factor, you could have
used the Rational
Root Theorem
and Remainder
Theorem to find the
full factorization.
For a review of
these theorems and
their application to
factoring polynomials,
see Chapter 1.
The potential solutions are a = 1, a = −2, and a = 2. Let’s test each one in the original equation.
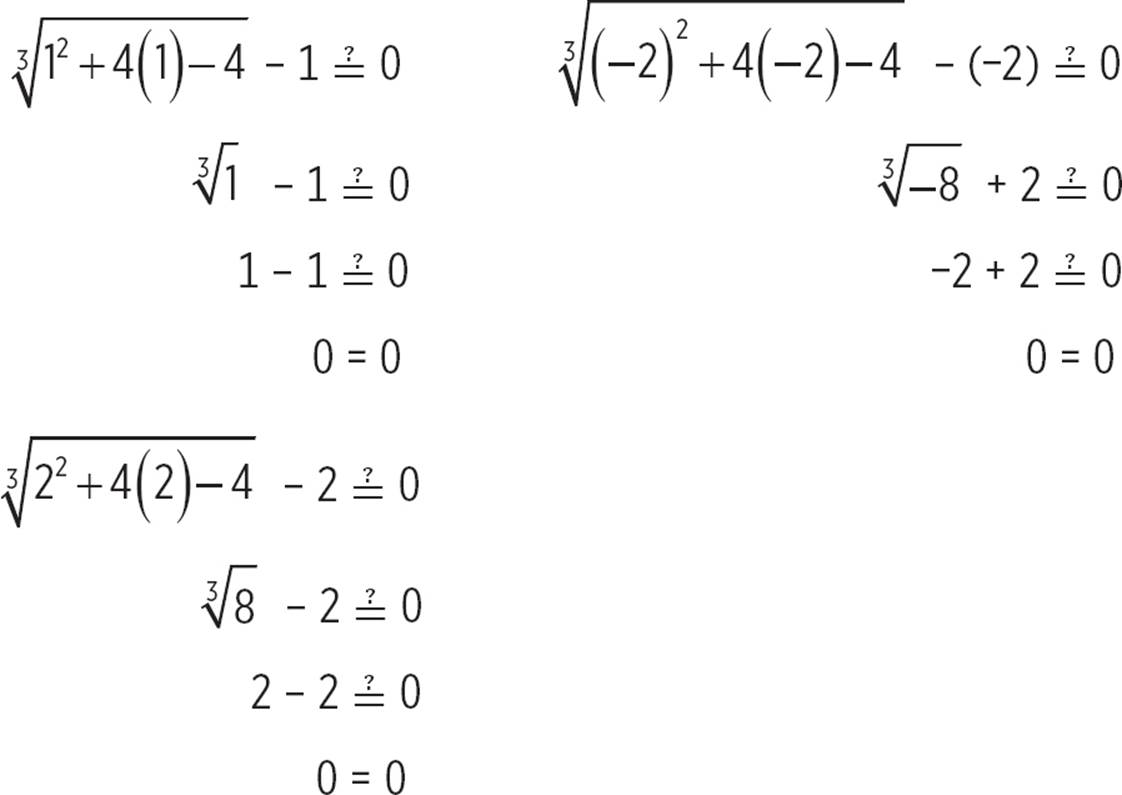
All three a-values produce true numerical equations, so all three are possible solutions. The possible solutions are −2, 1, and 2.
Notice the lack of
extraneous solutions?
Cubing a number
preserves its sign,
whether negative
or positive, so
cubing does not
produce extraneous
solutions the way
squaring or raising to
another even-degree
power might.


Here is how you may see radical equations on the ACT.
If 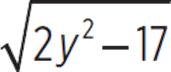 = y + 2, then what could be the value of y?
= y + 2, then what could be the value of y?
A. −3 and 7 only
B. 3 and 7 only
C. −3 only
D. 3 only
E. 7 only
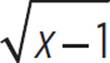 = x − 3
= x − 3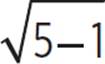 + 3 ≟ 5
+ 3 ≟ 5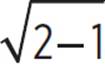 + 3 ≟ 2
+ 3 ≟ 2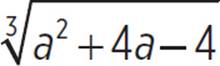 = a
= a