High School Algebra II Unlocked (2016)
Chapter 3. Radical and Rational Equations and Inequalities
Lesson 3.6. Radical Functions
REVIEW
The graph of a quadratic function is a parabola. It opens upward if the coefficient of x2 is positive and opens downward if the coefficient of x2 is negative.
If a constant is added to a function value, the function graph is translated vertically—up if the constant is positive, down if the constant is negative.
If a constant is added to every x-value in a function, the function graph is translated horizontally—to the left if the constant is positive, to the right if the constant is negative.
The Pythagorean Theorem states that the sum of the squares of the leg lengths of a right triangle is equal to the square of its hypotenuse: a2 + b2 = c2.
A radical function is a function that is defined as a radical expression.
In this lesson, we will only explore square root functions.

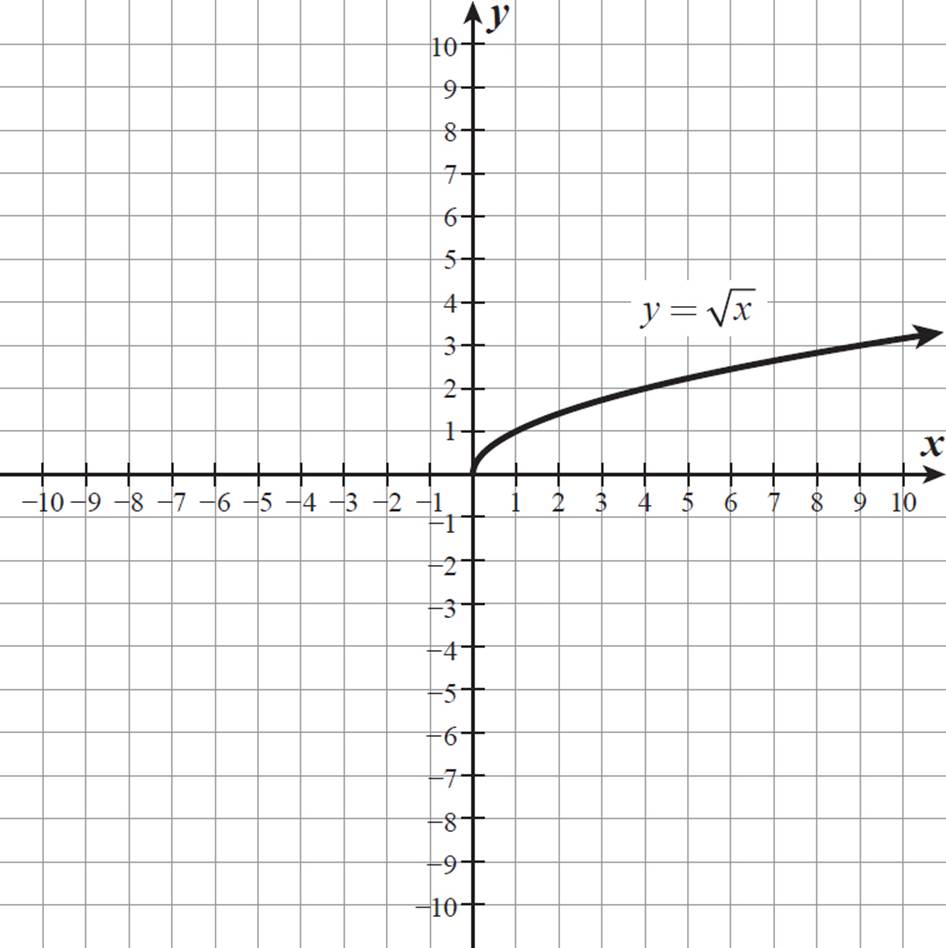
Graph the function y = 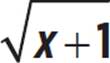 .
.
If we square both sides, we get y2 = x + 1, which we can rewrite as x = y2 − 1. This looks like a familiar quadratic equation, but it tells you how x is related to y, instead of how y is related to x. Remember how you graph quadratic functions.
The quadratic y = x2 − 1 looks like this.

When the variables are switched, as in x = y2 − 1, the relationship produces the same parabola but turned 90° clockwise. Actually, it is technically a reflection, not a rotation. When a function has its x and y variables switched, it gets reflected across the line y =x. The result for this parabola is the same, though. The graph of x = y2 − 1 is shown below.
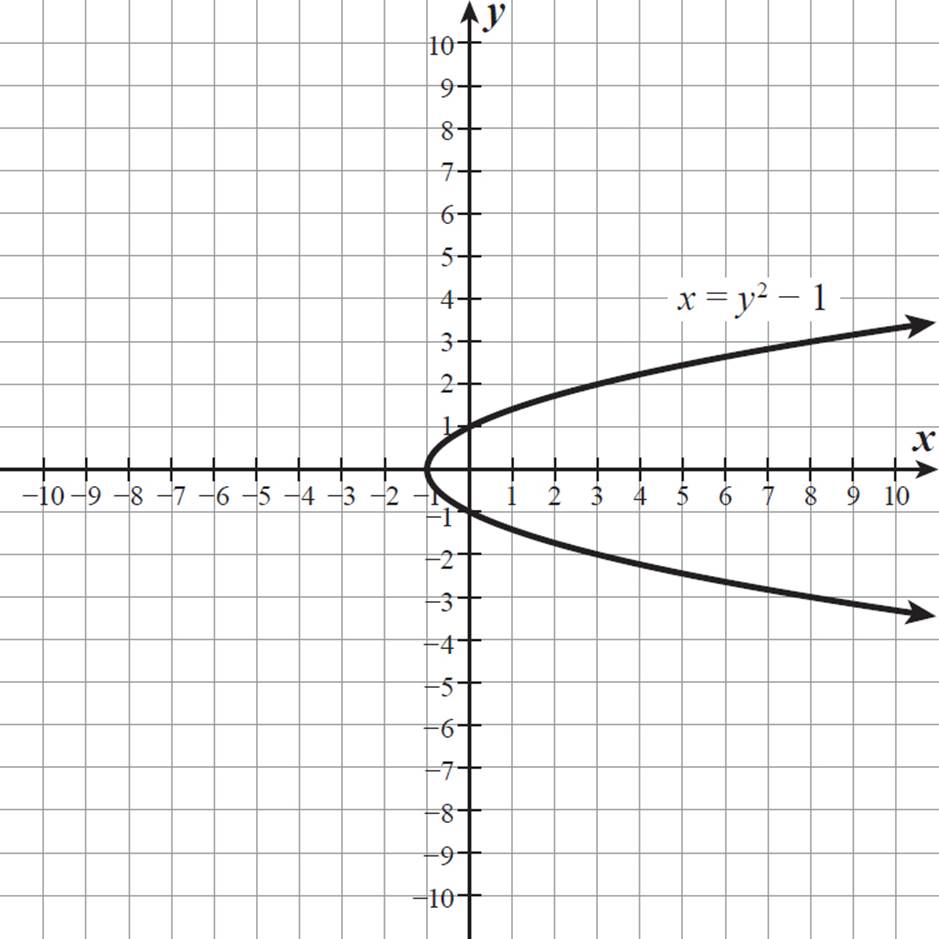
In the function
y = ![]() , the
, the
radicand cannot
be negative, so
x + 1 ≥ 0, which means
that x ≥ −1. This is
already evident in the
graph of x = y2 − 1.
However, the function y = 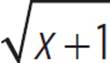 is not exactly the same as x = y2 − 1. We know that the value of a square root must be greater than or equal to 0, so
is not exactly the same as x = y2 − 1. We know that the value of a square root must be greater than or equal to 0, so 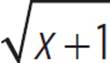 ≥ 0, or y ≥ 0. The half of the parabola that is below the x-axis represents negative y-values, so it is not included in the function y =
≥ 0, or y ≥ 0. The half of the parabola that is below the x-axis represents negative y-values, so it is not included in the function y = 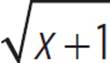 . The graph of y =
. The graph of y = 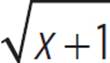 is the half of the parabola x = y2 − 1 that is above the x-axis.
is the half of the parabola x = y2 − 1 that is above the x-axis.

The point (−1, 0) on
the x-axis is included
in the function,
because a square root
can equal 0 (![]() = 0).
= 0).
The square root just
can’t be negative.

The domain of the function y = 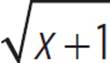 is x ≥ −1, as you can see from the graph (starting at x = −1 and continuing indefinitely to the right), as well as from the equation (x + 1 ≥ 0, because the radicand must be non-negative). The range of this function is y ≥ 0, as you can see from the graph (starting at y = 0 and continuing indefinitely upward), as well as from the equation (a square root, such as
is x ≥ −1, as you can see from the graph (starting at x = −1 and continuing indefinitely to the right), as well as from the equation (x + 1 ≥ 0, because the radicand must be non-negative). The range of this function is y ≥ 0, as you can see from the graph (starting at y = 0 and continuing indefinitely upward), as well as from the equation (a square root, such as 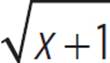 , must be 0 or any positive number).
, must be 0 or any positive number).
The graph of a basic square root function in the form f(x) = ![]() , where a is a constant, is half of a parabola.
, where a is a constant, is half of a parabola.
Another way to graph the function y = 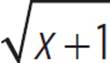 is to graph it as a translation of its parent function, y =
is to graph it as a translation of its parent function, y = 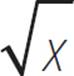 .
.

In Lesson 1.3, you
saw how changes to
x or to the function
value translate a
given polynomial
function. These rules
apply to any kind of
function, including
radical functions.
For any kind of function, including radical functions, the following translation rules apply for a function f(x) and constant k.
The graph of f(x) + k represents a vertical shift of the graph of f(x) by k units—up if k is positive, down if k is negative.
The graph of f(x + k) represents a horizontal shift of the graph of f(x) by k units—to the left if k is positive, to the right if k is negative.
In the case of y = 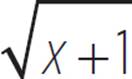 , a constant of 1 is added to x, inside the radicand, so the graph of y =
, a constant of 1 is added to x, inside the radicand, so the graph of y = 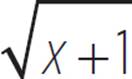 is the graph of y =
is the graph of y = 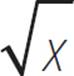 shifted 1 unit to the left.
shifted 1 unit to the left.

Graph the function h(x) = 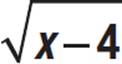 − 7.
− 7.
The parent function is y = ![]() . The constant 4 is subtracted from x, inside the radicand, so the graph of y =
. The constant 4 is subtracted from x, inside the radicand, so the graph of y = ![]() will be shifted 4 units to the right. The constant 7 is subtracted from the radical value, so the graph will be shifted 7 units down.
will be shifted 4 units to the right. The constant 7 is subtracted from the radical value, so the graph will be shifted 7 units down.
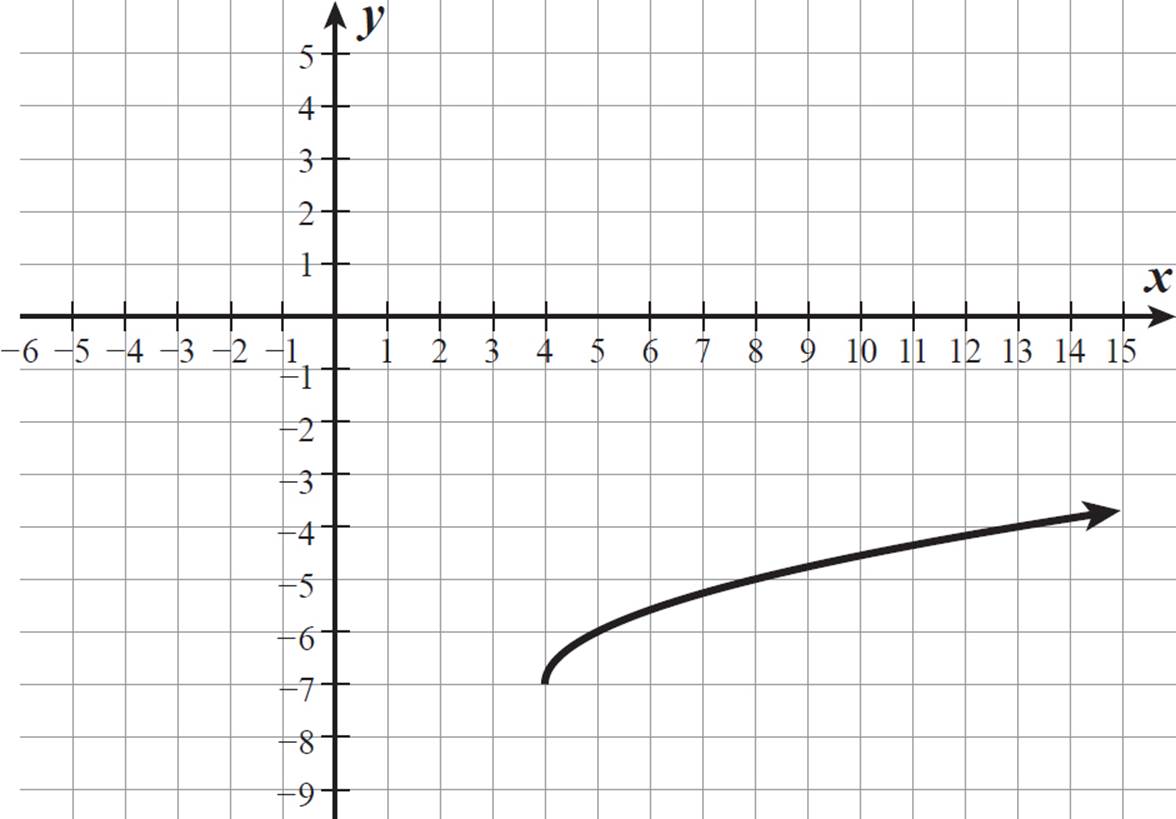
This is the graph of h(x) = 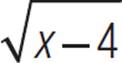 − 7. To make sure, let’s test values of x in the equation and see if the graph includes those points.
− 7. To make sure, let’s test values of x in the equation and see if the graph includes those points.
The radical 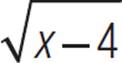 only exists as a real number when x − 4 ≥ 0, or x ≥ 4. That matches our graph, which starts at x = 4 and moves to the right.
only exists as a real number when x − 4 ≥ 0, or x ≥ 4. That matches our graph, which starts at x = 4 and moves to the right.
When x = 4, h(4) = ![]() − 7 = −7.
− 7 = −7.
When x = 5, h(5) = 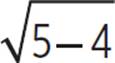 − 7 = −6.
− 7 = −6.
When x = 8, h(8) = 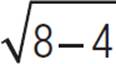 − 7 = −5.
− 7 = −5.
When x = 13, h(13) = 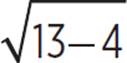 − 7 = −4.
− 7 = −4.
The equation produces the coordinate pairs (4, −7), (5, −6), (8, −5), and (13, −4), and the graph passes through each of these points. We have correctly graphed h(x) = 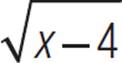 − 7.
− 7.

The function f(x) = 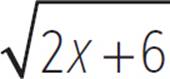 is not as easy to graph, because the parent function is not simply translated in this case. The magnitude of the half parabola is also affected, because x is multiplied by 2 in the radicand. However, we can still determine key characteristics of the graph of f(x) =
is not as easy to graph, because the parent function is not simply translated in this case. The magnitude of the half parabola is also affected, because x is multiplied by 2 in the radicand. However, we can still determine key characteristics of the graph of f(x) = 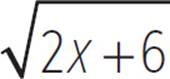 by looking at its equation.
by looking at its equation.

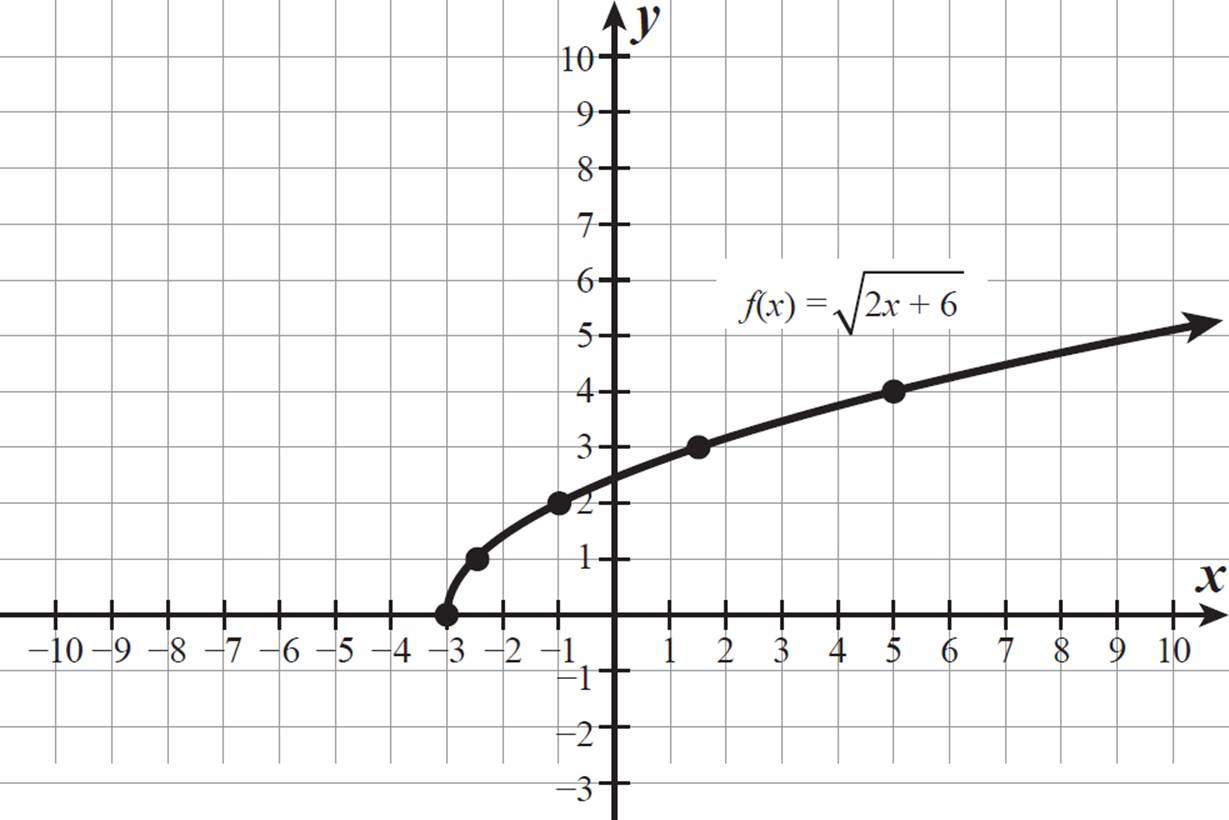
Graph the function f(x) = 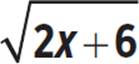 .
.
The smallest possible value of any square root is always 0, so the minimum value of f(x) is 0. This means that the lowest point on the graph of f(x) = 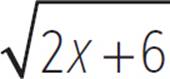 is on the x-axis (where f(x) = 0) and the rest of the graph is above the x-axis.
is on the x-axis (where f(x) = 0) and the rest of the graph is above the x-axis.
Let’s find the smallest possible value of x for this function. The value of the radicand must be greater than or equal to 0, so 2x + 6 ≥ 0.
|
2x ≥ −6 |
Subtract 6 from both sides. |
|
x ≥ −3 |
Divide both sides by 2. |
Since x-values for f(x) = 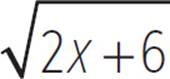 are always greater than or equal to −3, we know that the graph starts at x = −3 and moves to the right. The half parabola begins at the point (−3, 0) and curves up and to the right similarly to the y =
are always greater than or equal to −3, we know that the graph starts at x = −3 and moves to the right. The half parabola begins at the point (−3, 0) and curves up and to the right similarly to the y = ![]() function. We just need to find points that the graph passes through, to complete our graph. Choose values of x that make (2x + 6) a perfect square.
function. We just need to find points that the graph passes through, to complete our graph. Choose values of x that make (2x + 6) a perfect square.
When x = −5/2, f(−5/2) = 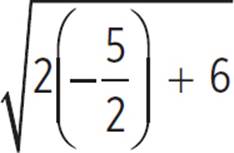 =
= ![]() = 1.
= 1.
When x = −1, f(−1) =  =
= ![]() = 2.
= 2.
When x = 3/2, f(3/2) = 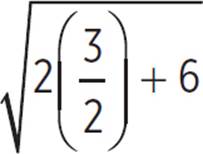 =
= ![]() = 3.
= 3.
When x = 5, f(5) = 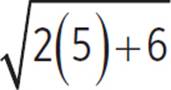 =
= 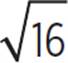 = 4.
= 4.
The graph begins at (−3, 0) and passes through (−5/2, 1), (−1, 2), (3/2, 3), and (5, 4).

RADICAL FUNCTIONS IN THE REAL WORLD
Radical functions may be useful for solving problems where the relationship involves one or more squared variables, such as a relationship described by the Pythagorean theorem.

Yimin is decorating a series of cards of various sizes by adding ribbons along their diagonals. Each card is a rectangle that is 7 centimeters longer than it is wide. Write a formula for the length of ribbon needed for a rectangular card in terms of the card’s width. If one card has a diagonal that is 3 centimeters more than twice the width of the rectangle, what are the dimensions of this rectangular card?
Let w = the width of the rectangular card, l = the length of the card, and d = the length of the diagonal of the card. The length is 7 centimeters longer than the width, so l = w + 7.
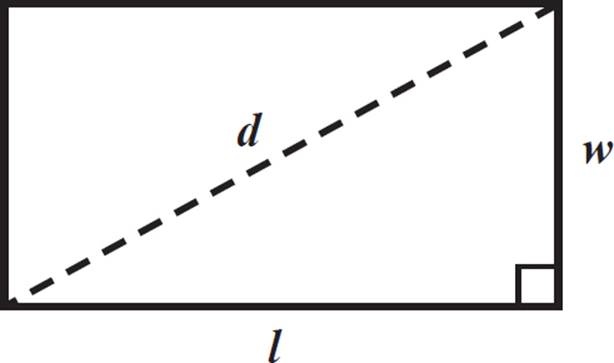
It’s often helpful to
draw diagrams to
visualize geometric
relationships.
As you can see from the diagram, the width, length, and diagonal of a rectangle form a right triangle, so we can write an equation using the Pythagorean theorem.
|
l2 + w2 = d2 |
|
|
d = |
Solve for d. |
|
d = |
Substitute (w + 7) for l. |
|
d = |
Expand the squared binomial in the radicand. |
|
d = |
Combine like terms. |
This formula gives the length, d, of ribbon needed for a card of width w in Yimin’s collection.
If the diagonal of a card is 3 centimeters more than twice the width, then d = 2w + 3. We can substitute (2w + 3) for d in our radical function equation.
|
2w + 3 = |
|
|
(2w + 3)2 = 2w2 + 14w + 49 |
Square both sides. |
|
4w2 + 12w + 9 = 2w2 + 14w + 49 |
Expand the squared binomial. |
|
2w2 − 2w − 40 = 0 |
Move all terms to one side. |
|
w2 − w − 20 = 0 |
Divide both sides by 2. |
|
(w + 4)(w − 5) = 0 |
Factor the quadratic. |
The solutions to the equation are w = −4 and w = 5. However, a card cannot have a negative length for either side length, so the width cannot equal −4. This is an extraneous solution. In fact, if you test w = −4 in the equation 2w + 3 = 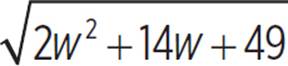 , you will get a false numerical equation (−5 = 5).
, you will get a false numerical equation (−5 = 5).
The solution is w = 5. The width of the card is 5 centimeters. The length of the card is 5 + 7 = 12 centimeters. The diagonal of the card, or the length of the ribbon needed for this card, is 2(5) + 3 = 13 centimeters.

We could also solve by graphing a system of equations, after correctly translating the given information into equations. Here is our system of equations relating the variables d and w.
d = 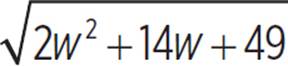
d = 2w + 3
Notice that the radical
function is a different
shape from most of the
ones we have looked at
so far. Having an x2 (or
w2, in this case) within
the radicand produces
a very different
graph. Graphing
technology is great
for these situations!
Using graphing technology, we can graph both functions on the same coordinate grid.
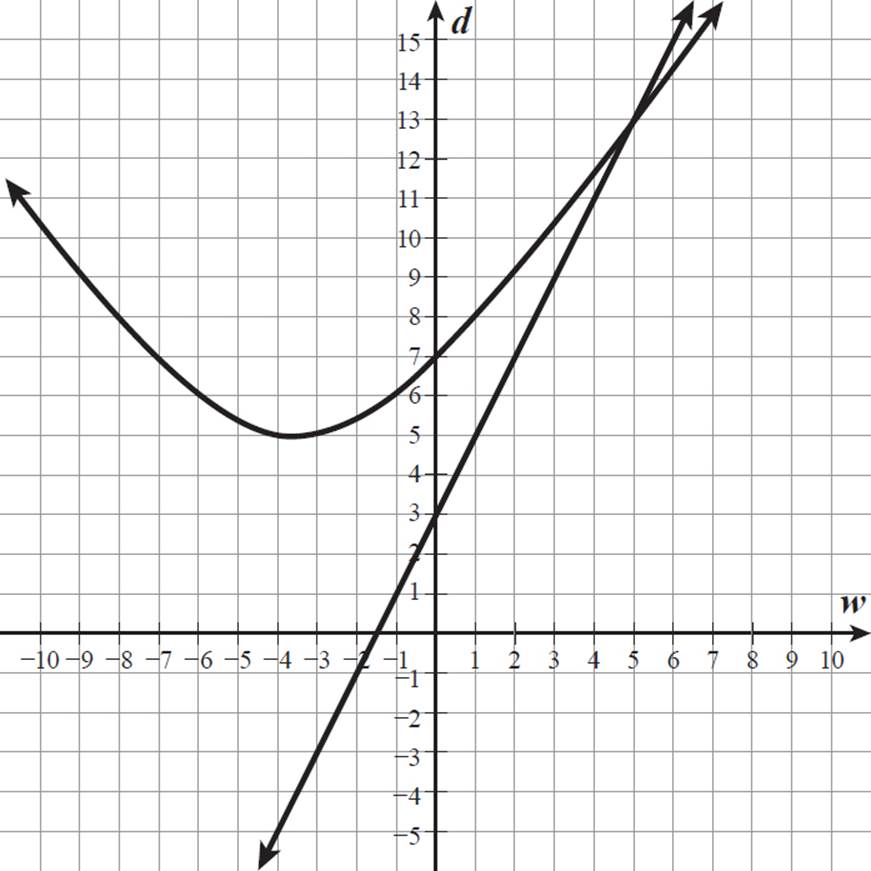
The two graphs intersect at the point (5, 13), so the solution to the system of equations is w = 5, as we found algebraically. The width of the card is 5 centimeters. The d-value of this point of intersection is 13, so the length of the diagonal, the length of the ribbon, is 13 centimeters. The length of the card is 7 centimeters more than its width, or 12 centimeters.
DRILL
CHAPTER 3 PRACTICE QUESTIONS
Click here to download a PDF of Chapter 3 Practice Questions.
Directions: Complete the following open-ended problems as specified by each question stem. For extra practice after answering each question, try using an alternative method to solve the problem or check your work.
1. Solve the equation and check your solution. 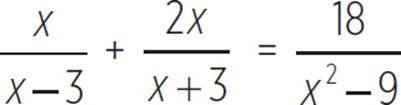
2. Sketch the graph of f(x) = 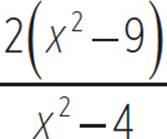 by discussing asymptotes, intercepts, symmetry, and finding a couple of additional points to plot. Use a calculator to check your graph.
by discussing asymptotes, intercepts, symmetry, and finding a couple of additional points to plot. Use a calculator to check your graph.
3. Find all real solutions of 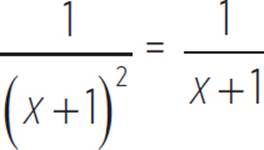 + 2.
+ 2.
4. Find all real solutions to 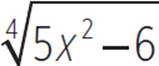 = x.
= x.
5. Solve ![]() − 1 =
− 1 = 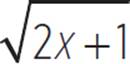 and check the solution(s).
and check the solution(s).
6. Solve  < 2 and check the solution.
< 2 and check the solution.
7. The length of a rectangle is 7 units more than its width. Find the range of values for the length and the width if the ratio of the length to the width is no more than 10 and at least 5.
8. On her first ski run this morning, Mitsue skied a 0.3-mile trail. The second trail she skied was twice as long and steeper, and her speed on it was 1.5 times as fast as her speed on the first trail. Her ski time for the second trail was half a minute more than her time for the first trail. Write an equation for t, Mitsue’s time on the first trail, as a function of r, her skiing speed on the first trail. Write another equation to represent her second trail run, in terms of the same values of t and r. What was Mitsue’s skiing speed, in miles per hour, for each of the two trails?
9. Jean-Luc needs to install a new cylindrical storage tank water heater. To minimize how much space it takes in his basement, he plans to get the tallest one possible that will fit, which is 5 feet 3 inches high. Write a function for r, the radius, in feet, of a storage tank of height 5 feet 3 inches, in terms of v, the volume of water, in cubic feet, that it holds. Jean-Luc decides to get an 80-gallon storage tank. If one cubic foot contains 7.48 gallons, what is the diameter of the storage tank he chose?
SOLUTIONS TO CHAPTER 3 PRACTICE QUESTIONS
1. −2
Multiply each side by the lowest common denominator of (x + 3)(x − 3):
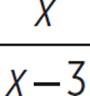 (x + 3)(x − 3) +
(x + 3)(x − 3) + 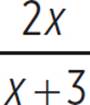 (x + 3)(x − 3) =
(x + 3)(x − 3) = 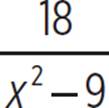 (x + 3)(x − 3)
(x + 3)(x − 3)
x(x + 3) + 2x(x − 3) = 18
x2 + 3x + 2x2 − 6x = 18
3x2 − 3x = 18
3x2 − 3x − 18 = 0
3(x2 − x − 6) = 0
3(x − 3)(x + 2) = 0
x = 3 ; x = −2
Don’t stop here! Now, check the solutions in the original equation. If 3 is plugged back in for x, then there is a zero in the denominator of two expressions, which means that 3 is an extraneous solution. So, check −2:
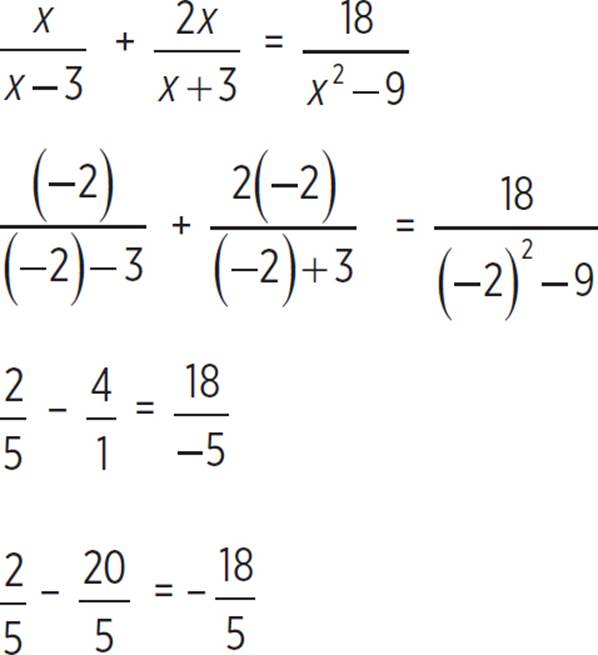
The statement is true, so the solution is x = −2.
2.
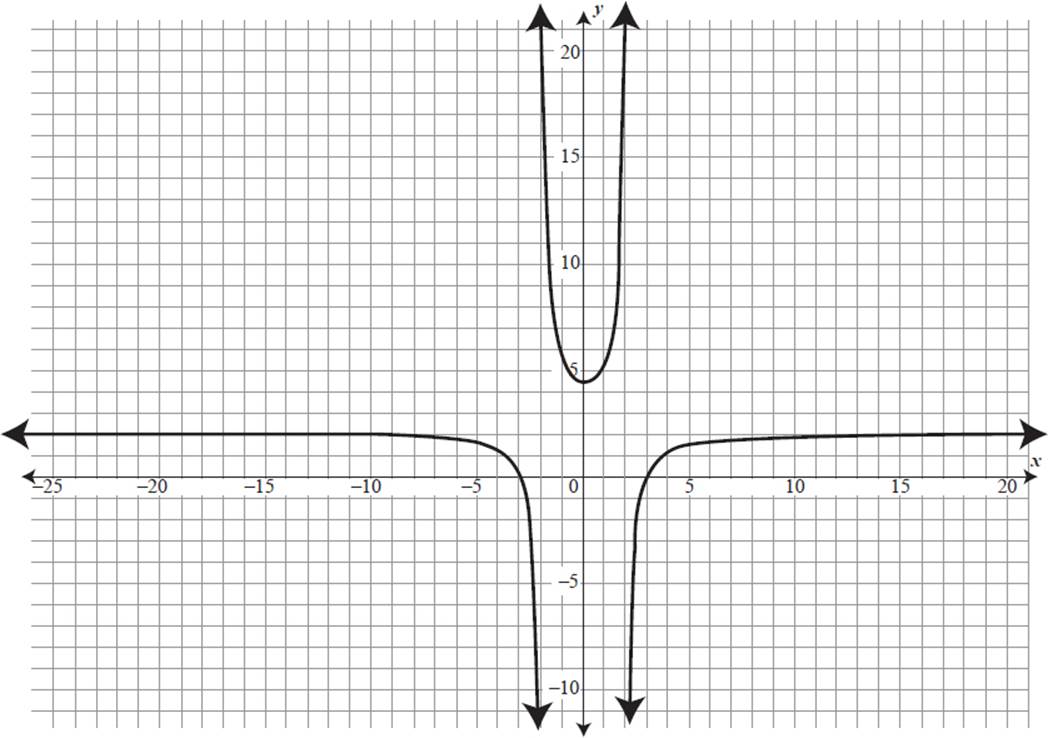
To sketch the graph, begin by finding the x- and y-intercepts. Factor the numerator and denominator of the given equation:
f(x) = 
To find the y-intercept, set x = 0:
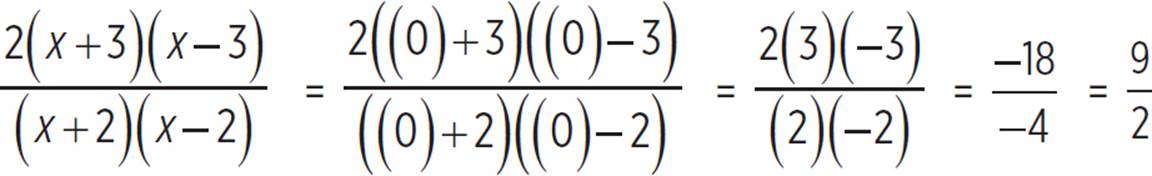
So, the y-intercept is at (0, ![]() ).
).
To find the x-intercept(s), set y = 0 and solve for x-values that make the numerator equal 0:
0 = 2(x + 3)(x − 3)
0 = x + 3 ; 0 = x − 3
−3 = x ; 3 = x
So, the x-intercepts are at (±3, 0).
Next, proceed to find the vertical and horizontal asymptotes. Find the vertical asymptote(s) by setting the denominator equal to zero and solving:
(x + 2)(x − 2) = 0
x + 2 = 0 ; x − 2 = 0
x = −2 ; x = 2
So, the vertical asymptotes occur at x = ±2.
Find the horizontal asymptote by comparing the degrees of the polynomials in the numerator and the denominator. Since the degrees are equal to each other (degree 2), look to the leading coefficients:
![]() = 2
= 2
So, the horizontal asymptote is at y = 2.
Check for symmetry with respect to the y-axis by finding f(−x):
f(x) = 
f(-x) = 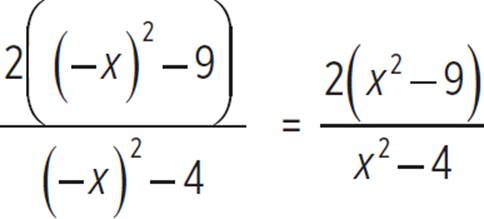
Since f(−x) = f(x), the function is even and has y-axis symmetry.
Plug in a couple of test values, such as x = 1 and x = 4, to see the 'margin-top:0cm;margin-right:0cm;margin-bottom:0cm; margin-left:20.6pt;margin-bottom:.0001pt;line-height:24.0pt'>f(1) = 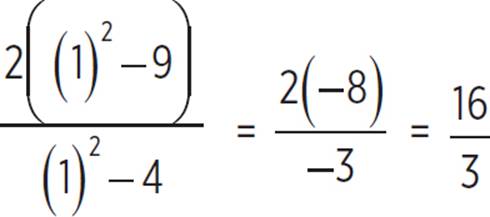
f(4) = 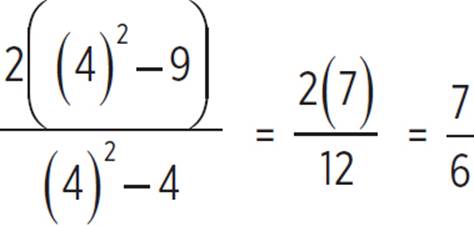
Finally, use the information gathered to sketch the graph.
3. x = −2,−1/2
The least common denominator of the three terms in this equation is (x + 1)2.
|
|
Convert each term to have the lowest common denominator. |
Since all denominators are the same, set the numerators of the left and right sides equal to each other. Note that x ≠ −1 since the denominator will equal zero at that x-value.
|
1 = (x + 1) + 2(x + 1)2, x ≠ −1 |
|
|
1 = x + 1 + 2(x2 + 2x + 1) |
Expand the squared binomial using FOIL. |
|
1 = x + 1 + 2x2 + 4x + 2 |
Distribute 2 to each term in parentheses. |
|
0 = 2x2 + 5x + 2 |
Subtract 1 from both sides and combine like terms. |
Next, to determine the solutions, factor the quadratic and set each term equal to zero. (The quadratic formula could also be used with a = 2, b = 5, and c = 2.)
0 = 2x2 + 5x + 2
0 = (2x + 1)(x + 2)
2x + 1 = 0 ; x + 2 = 0
x = −1/2 ; x = −2
The solutions are x = −2 and x = −1/2.
4. x = ![]() ,
, ![]()
To tackle this problem, clear out the radical by raising both sides to the fourth power:![]() = x
= x
![]() = (x)4
= (x)4
5x2 − 6 = x4
Next, get the expression equal to zero by moving all terms to one side:
5x2 − 6 = x4
0 = x4 − 5x2 + 6
The terms are in decreasing order of exponents and can be factored:
|
0 = x4 − 5x2 + 6 |
Quadratic in form of a2 − 5a + 6 |
|
0 = (x2 − 3)(x2 − 2) |
Factored form of (a − 3)(a − 2) |
Set each factor equal to zero and solve for x:
|
0 = x2 − 3 ; 0 = x2 − 2 |
|
|
3 = x2 |
2 = x2 |
|
± |
± |
Don’t stop there! Remember to check your solutions by plugging back into the original equation. The expression on the left-hand side of the equation is an even root, so it will always produce a positive value. The negative roots would produce a positive fourth-root expression on the left side of the equation and a negative expression on the right side (x), so they fail the check. So, check x = ![]() and
and ![]() :
:


Therefore, the solutions are x = ![]() and x =
and x = ![]() .
.
5. No solution.
Square both sides of the given equation to begin removing the square root:
|
|
Given. |
|
( |
Square both sides. |
|
x − 2 |
FOIL the left-hand side. |
|
−2 |
Combine like terms. |
Repeat the process of squaring both sides to remove the radical:
|
−2 |
|
|
(−2 |
Square both sides. |
|
4x = x2 |
|
|
0 = x2 − 4x |
Subtract 4x from both sides. |
|
0 = x(x − 4) |
Factor. |
|
0 = x ; 0 = x − 4 |
Set each term equal to 0. |
|
0 = x ; 4 = x |
Solve for x. |
Don’t stop there! Check both solutions!

Since both solutions failed the check, the equation ![]() − 1 =
− 1 = 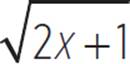 has no real solutions. An alternative way to solve this equation is by graphing the system of equations y =
has no real solutions. An alternative way to solve this equation is by graphing the system of equations y = ![]() − 1 and y =
− 1 and y = 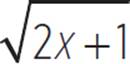 , as shown below. Any solution to the equation
, as shown below. Any solution to the equation ![]() − 1 =
− 1 = 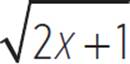 corresponds to an intersection of these two functions.
corresponds to an intersection of these two functions.

The two graphs never intersect. As x increases, the value of 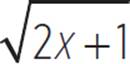 increases more quickly than the value of
increases more quickly than the value of ![]() − 1, so the graphs get farther and farther apart.
− 1, so the graphs get farther and farther apart.
6. −1 ≤ x < 3
Begin by squaring both sides to remove the radical. This yields x + 1 < 4, which can be simplified to x < 3.
Squaring both sides sometimes produces an incorrect solution set, so we must test values on either side of 3, to make sure that x < 3 is correct.
When x = 0, the inequality becomes 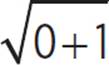 < 2, which simplifies to 1 < 2. This is true.
< 2, which simplifies to 1 < 2. This is true.
When x = 8, the inequality becomes 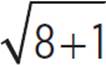 < 2, which simplifies to 3 < 2. This is false.
< 2, which simplifies to 3 < 2. This is false.
The inequality x < 3 seems true. However, take a look back at the original function. Since there is a square root involved, the radicand cannot be negative. To finish out the solution, it must be determined where x + 1 ≥ 0:
x + 1 ≥ 0
x ≥ −1
So, the solution is −1 ≤ x < 3.
7. 70/9 ≤ l ≤ 35/4 and 7/9 ≤ w ≤ 7/4
First, determine expressions for the dimensions of the rectangle. Since the length is 7 more than the width, the width can be expressed as x and the length can be expressed as x + 7. Given that the ratio of the length to the width is at least 5 and no more than 10, an inequality can be set up as follows:
5 ≤ 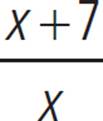 ≤ 10
≤ 10
Begin solving the inequality by multiplying both all three expressions by x:
5x ≤ x + 7 ≤ 10x
Solve by splitting the inequality up into two pieces:
|
5x ≤ x + 7 |
and |
x + 7 ≤ 10x |
|
4x ≤ 7 |
7 ≤ 9x |
|
|
x ≤ 7/4 |
7/9 ≤ x |
So, the range of possible values for the width, x, is 7/9 ≤ x ≤ 7/4. Since the length is 7 more than the width, the possible range for the length, x + 7, can be found by adding 7:
7/9 + 7 ≤ x + 7 ≤ 7/4 + 7
70/9 ≤ x + 7 ≤ 35/4
The dimensions of the rectangle are length l and width w given by 70/9 ≤ l ≤ 35/4 and 7/9 ≤ w ≤ 7/4.
8. 12 miles per hour, 18 miles per hour
This situation uses the distance = rate × time relationship. To write an equation for t as a function of r, rewrite the d = rt equation as t = d/r. On Mitsue’s first ski run this morning, she skied a distance of 0.3 mile, so the function t = 0.3/r describes the run.
On the second trail she skied, the distance was twice as long: 2 ⋅ 0.3 = 0.6 mile. Her speed was 1.5 times as fast: 1.5r. Her time was half a minute more: t + 0.5. Use these new values in the t = d/r relationship.
t + 0.5 = 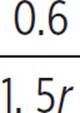
Notice that t still represents Mistue’s time, in minutes, on the first trail, and r still represents her speed on the first trail. Because these values are consistent, we can solve this system of two equations to find t and r.
|
t = |
Subtract 0.5 from both sides of the equation for the second trail. |
|
0.3/r = |
Substitute the expression for t from the first trail equation, t = 0.3/r. |
|
0.45 = 0.6 − 0.75r |
Multiply both sides of the equation by the LCD, 1.5r. |
|
−0.15 = −0.75r |
Subtract 0.6 from both sides. |
|
0.2 = r |
Divide both sides by −0.75. |
All values have been given in miles and minutes, so this solution means that Mitsue’s speed on the first trail was 0.2 mile per minute. To convert to miles per hour, multiply by 60 minutes/hour: 0.2 ⋅ 60 = 12. Mitsue’s speed on the second trail was 1.5 times this speed: 1.5 ⋅ 12 = 18. Her speed on the first trail was 12 miles per hour, and her speed on the second trail was 18 miles per hour.
9. 1.6 feet
The shape of each storage tank is a cylinder, and the volume of a cylinder is given by πr2h, where r is the radius and h is the height. Jean-Luc wants a storage tank that is 5 feet 3 inches high. Convert this height to feet: 5 3/12 feet, or 5.25 feet. With h = 5.25, we can write the volume formula as v = 5.25πr2. To write a function for r in terms of v, solve this equation for r.
|
|
Divide both sides by 5.25π. |
|
|
Take the square root of both sides. |
In this situation, r is a measurement of the radius, so it must be positive.
Instead of volume in cubic feet, we are given the capacity of the water tank in gallons, 80 gallons. We must convert gallons to cubic feet to substitute for v in our formula.
80 gallons ÷ 7.48  ≈ 10.7 cubic feet
≈ 10.7 cubic feet
|
r = |
Substitute 10.7 for v in the radius function. |
|
r ≈ 0.8 |
Use your calculator to evaluate |
The diameter is twice the radius: 2 ⋅ 0.8 = 1.6. Jean-Luc chose a storage tank that is 1.6 feet in diameter.
REFLECT
Congratulations on completing Chapter 3! Here’s what we just covered. Rate your confidence in your ability to:
•Solve single-variable rational and radical equations and inequalities
1 2 3 4 5
•Write and solve rational and radical equations, inequalities, and functions to describe real-life situations and solve problems
1 2 3 4 5
•Graph rational and radical functions
1 2 3 4 5
•Use systems of equations to solve single-variable rational and radical equations
1 2 3 4 5
If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.
 Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.
Access your online student tools for a handy, printable list of Key Points for this chapter. These can be helpful for retaining what you’ve learned as you continue to explore these topics.
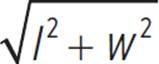
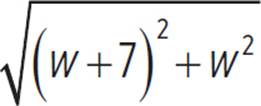
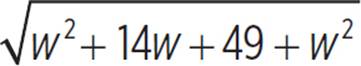
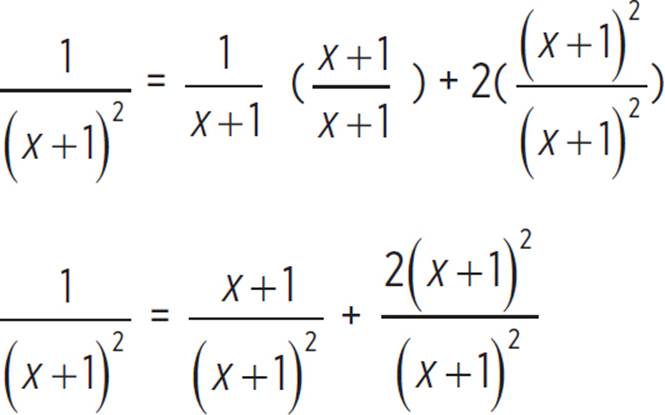
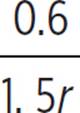 − 0.5
− 0.5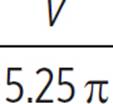 = r2
= r2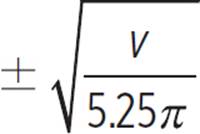 = r
= r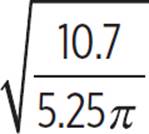
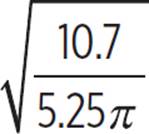 .
.