High School Algebra II Unlocked (2016)
Chapter 4. Trigonometric Functions
Lesson 4.2. Radians
REVIEW
Angles can be measured from 00 to 3600. Those that are less than 900 are called acute, while those that are between 900 and 1800 are obtuse. Right angles are exactly 900, and straight angles are exactly 1800.
Triangles can be defined either by their angles (a right triangle has a right angle) or sides (an isosceles triangle has two equal sides).
A radius of a circle is any line segment connecting a point on the circle to the center of the circle. The radius of a circle is also defined as the length of any radius of the circle.
The diameter of a circle is a line segment passing through the center of the circle, with both endpoints on the circle. The length of the diameter is twice the radius.
The circumference of a circle is the distance around the circle and is equal to 2πr, where r is the length of the radius of the circle. An arc is a portion of that circumference.
A 30-60-90 triangle is a right triangle with angle measures of 30°, 60°, and 90°, and has side lengths in the ratio 1: ![]() :2, respectively opposite each of those angles.
:2, respectively opposite each of those angles.
Degrees and radians are two different units used to express angle measurements. Radians are defined in relationship to a circle, as measuring a central angle of the circle. A central angle is an angle formed by two radii of the circle. Its vertex is the center of the circle.
The radian measure of a central angle of a circle is the ratio of the length of the circular arc the angle subtends to the radius of the circle.
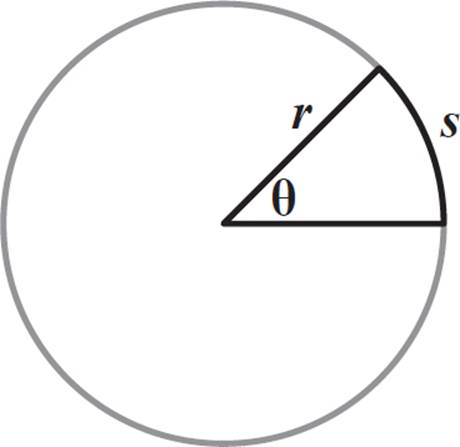
The circular arc subtended by the central angle is the portion of the circle between the endpoints of the radii that form the angle. In the diagram below, the central angle is labeled as θ, a radius is labeled as r, and the subtended arc is labeled as s.
All radii of a circle
are congruent, so
the unlabeled radius
forming the other side
of the central angle is
the same length, r.
So, the measure of θ in radians is s/r, where s is the arc length and r is the radius.
A minor arc is an arc subtended by a central angle of less than 180°, and a major arc is an arc subtended by a central angle of more than 180°. For any given two points on a circle, the minor arc and the major arc connecting them make up the entire circle. The minor arc is the shorter path between them, and the major arc is the longer path.
When two points on
a circle are endpoints
of the same diameter,
then the two arcs
connecting them
are each exactly
180° and neither is
minor nor major.

In the diagram below, circle P has a diameter of 12 units. If minor arc QR has a measure of 4π, what is the measure of ∠QPR in radians?
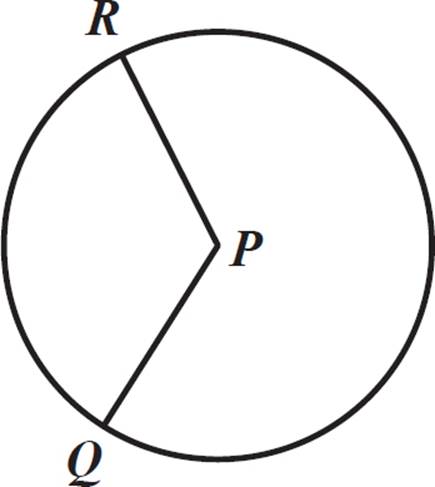
Minor arc QR is the shorter arc connecting points Q and R. We know from the definition of radian measure that the measure of angle QPR in radians equals s/r. The arc length of arc QR is 4π. The diameter of circle P is 12, so its radius is 6.
|
m∠QPR = s/r |
Use the definition of radian measure to write an equation. |
|
m∠QPR = 4π/6 |
Substitute 4π for s and 6 for r. |
|
m∠QPR = 2π/3 |
Simplify the fraction. |
The measure of angle QPR is 2π/3 radians.
The expression 2π/3
is the same as 2/3 π.
The π can be written as
part of the fraction, in
the numerator, or can
follow the fraction.

RADIANS AND DEGREES
A complete revolution of a circle is 360 degrees (360°). According to the definition of radian measure, the radian measure of a complete revolution of a circle is equal to the circumference of the circle divided by its radius. The circumference of a circle is given by the expression 2πr, so the radian measure of a full-circle central angle is 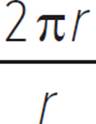 , which simplifies to 2π. So, 360° is equivalent to 2π radians.
, which simplifies to 2π. So, 360° is equivalent to 2π radians.
180° = π radians
Divide both sides of
the ratio 360:2π by 2
to get the simplified
ratio 180:π.

25/11 π radians is approximately equal to how many degrees?
To convert from radians to degrees, we must multiply by 180/π.
|
|
|
|
|
Cancel out the common factor of π in the numerator and denominator. |

Converting between
radians and degrees
is just like switching
between units of
measurement like
inches and feet.
Remember to carefully
label units as you
convert, and cancel
out units that overlap.
In this example,
radians will cancel
out, leaving degrees.

Here is how you may see radians on the SAT.
In the figure to the right, circle O has a radius of 4, and angle XOY measures ![]() π radians. What is the measure of minor arc XY?
π radians. What is the measure of minor arc XY?
A) ![]() π
π
B) 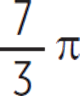
C) 7π
D) 12π
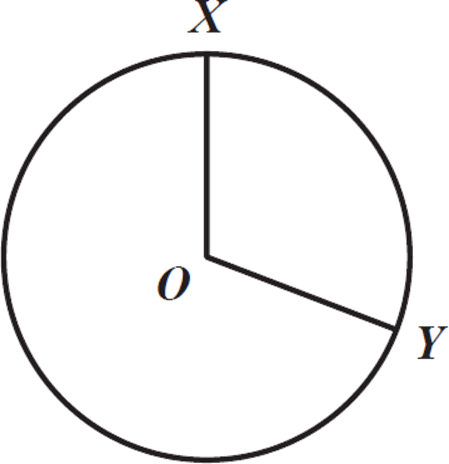
|
|
Multiply to combine fractions. |
|
408.09 |
Calculate fraction value. |
25/11 π is approximately equal to 409°.
Notice that the angle
measure is greater
than 360°, or 2π.
It is possible, in
trigonometry, to have
angles that measure
more than a full
revolution of a circle.


What is the measure, in radians, of an acute angle of an isosceles right triangle?
An isosceles right triangle is also known as a 45-45-90 triangle, because its angles measure 45°, 45°, and 90°. Each acute angle measures 45°, so we must convert 45° to radians.
|
45 degrees × |
|
|
45π/180 |
Multiply. |
|
π/4 |
180 is the same as 4 ⋅ 45, so we can cancel out the common factors of 45. |
An acute angle of an isosceles right triangle, or a 45° angle, has a measure of π/4 radians.
This time π is on top
and 180 is on the
bottom, because we
are “canceling out”
degrees in the unit
labels, converting
to radians.

RADIANS AND UNIT CIRCLES
Although radians measure central angles of circles of any radius (such as in Example 3), mathematicians tend to use the unit circle—a circle of radius 1 unit—for work involving radians. Why is that? Well, take a look at the relationship of radians to arc length and radius, θ = s/r. When the radius, r, equals 1, the equation becomes simply θ = s.
The radian measure of an angle is equal to the length of the arc on the unit circle subtended by the angle.

Shown below is a sector of a unit circle. What is the length of arc EF?
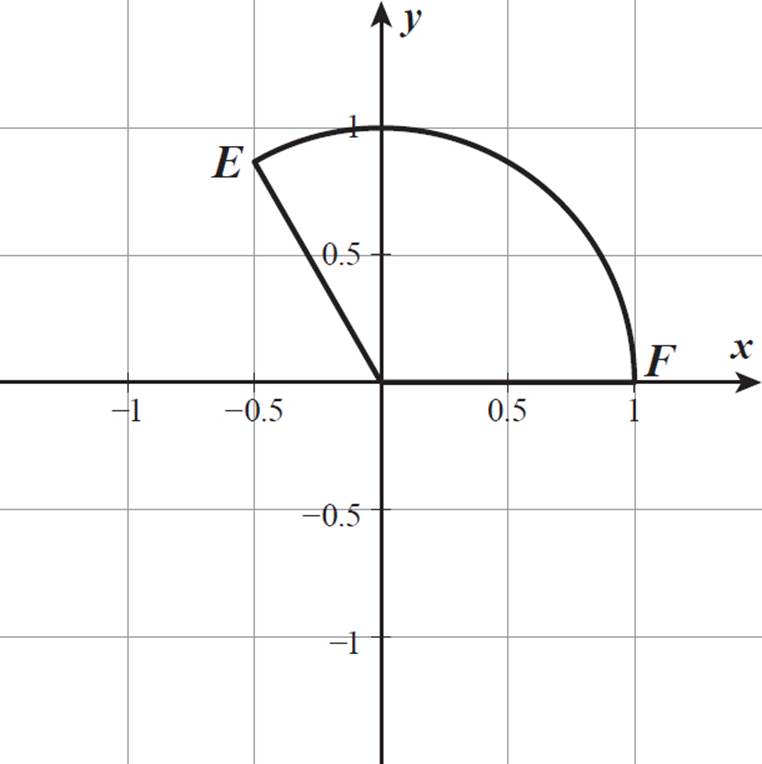
To find the length of the arc, we have to find the measure of its central angle, in radians. We know that it is greater than π/2, or 90°, because the section in the first quadrant, between the x-axis and y-axis, is a right angle. The measure of the additional portion to the left of the y-axis is what we must find.
Notice that point E has an x-value of −1/2, which means that it is exactly 1/2 unit away from the y-axis. When we draw this direct distance as a horizontal line, we form a triangle with the angle side and the y-axis.

We know that the measure of angle XOY in radians equals s/r. The angle measure is 7/12 π radians, and the radius is 4.
|
m∠XOY = s/r |
|
|
|
Substitute 7/12 π for m∠XOY and 4 for r. |
|
4 · |
Multiply both sides by 4. |
|
|
Cancel out the common factor of 4 in the numerator and denominator. |
Minor arc XY has a measure of 7/3 π. The correct answer is (B).
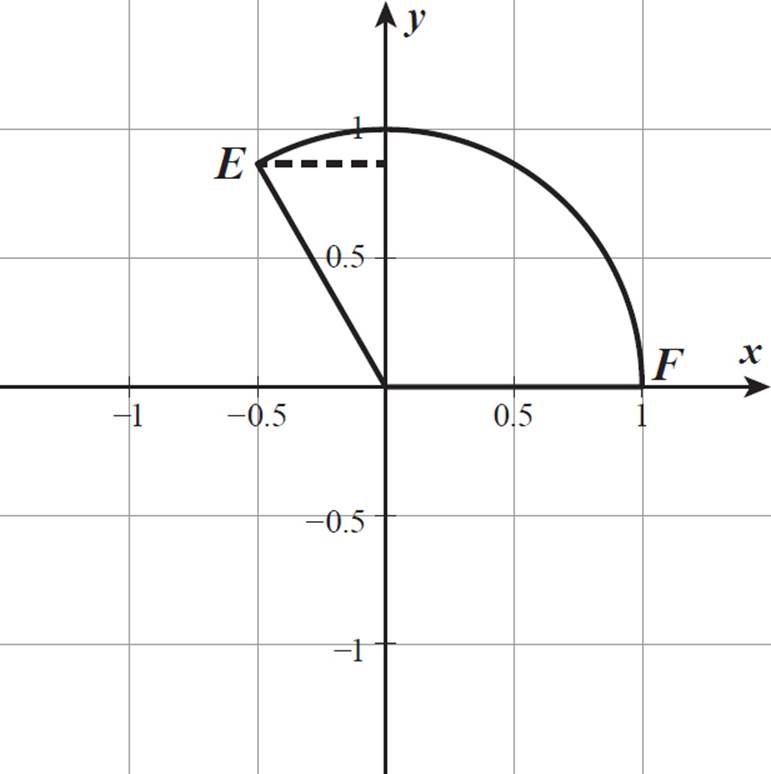
This is a right triangle, because the horizontal dashed line and the vertical y-axis are perpendicular. The length of the diagonal side of the triangle is 1 unit, because it is a radius of a unit circle. The short side is 1/2 unit long, because this is the distance from point E to the y-axis.
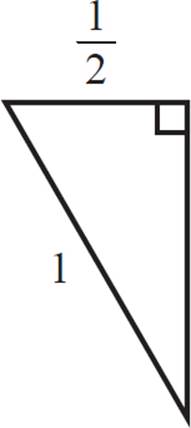
Does this look familiar? When the hypotenuse of a right triangle is twice as long as its shorter leg, you know that it must be a 30-60-90 right triangle. In our triangle, the hypotenuse length, 1, is 2 times the leg with length 1/2, so the angle opposite that leg measures 30°.
Now we know that the angle of the sector is 90° + 30° = 120°. Convert this measure to radians.
120° × 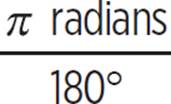 = 2/3 π radians
= 2/3 π radians
The angle of the sector measures 2/3 π, so the length of the unit circle arc EF is also 2/3 π.

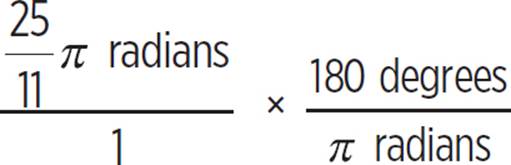
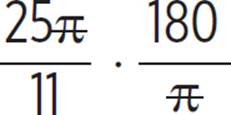
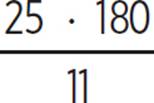
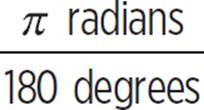
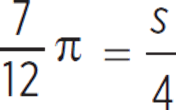
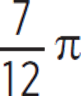 = s
= s