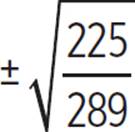High School Algebra II Unlocked (2016)
Chapter 4. Trigonometric Functions
Lesson 4.5. Trigonometric Function Identities
REVIEW
The equation of a circle centered at the origin, with radius r, is x2 + y2 = r2.
COMMUTATIVE PROPERTY OF ADDITION: a + b = b + a
As with polynomials, there are identities that relate the various trigonometric functions to one another. We already described several of them earlier in this chapter, such as csc θ = 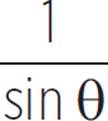 , sec θ =
, sec θ = 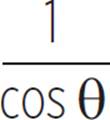 , and cot θ =
, and cot θ = 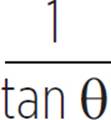 . Each of these represents an inverse relationship, so we can rewrite them as sin θ =
. Each of these represents an inverse relationship, so we can rewrite them as sin θ = 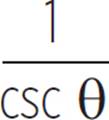 , cos θ =
, cos θ = 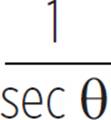 , and tan θ =
, and tan θ = 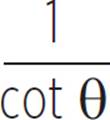 .
.

Here is how you may see trigonometric function graphs on the ACT.
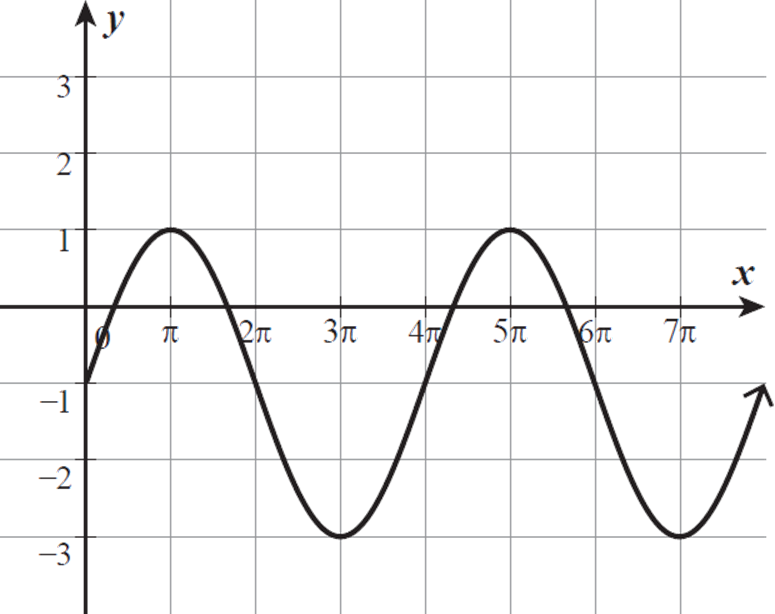
Which of the following equations describes the equation graphed below?
A. y = sin x/2
B. y = −1 + sin x/2
C. y = −1 + 2 sin x/2
D. y = 2 sin x
E. y = −1 + 2 sin x

Write an identity for tan θ in terms of two other trigonometric functions.
Tangent is defined as  . Another trigonometric function that involves the leg opposite the given angle is sine, which is
. Another trigonometric function that involves the leg opposite the given angle is sine, which is 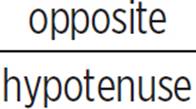 . The cosine is defined as
. The cosine is defined as  . Let’s divide sin θ by cos θ.
. Let’s divide sin θ by cos θ.
|
|
Write each trigonometric function as its ratio. |
|
|
Rewrite the division as multiplication by the reciprocal of the divisor. |
|
|
Cancel out the common factor in the numerator and denominator. |
|
|
Multiply. |
|
tan θ |
Use the definition of tangent. |
Another way to write
an identity for tan θ is
tan θ = 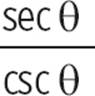 .
.
You can prove this
using the same steps
we used to prove
that tan θ = 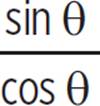 .
.
Another way to write sin θ ÷ cos θ is as the fraction 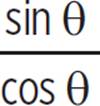 . So, our identity can be written as tan θ =
. So, our identity can be written as tan θ = 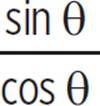 .
.

Another identity that we have already explored within this chapter is cos θ = sin (π/2 − θ). Likewise, sin θ = cos (π/2 − θ). Similar identities exist for the other trigonometric functions as well.
An easy way to remember these identities is to reference a right triangle, such as triangle ABC at the beginning of this chapter. The cosine of an angle is equal to the sine of its complementary angle. The sine of an angle is equal to the cosine of its complementary angle. These identities are just extended to all possible value of θ.
Here is a list of some useful trigonometric function identities.

Any true equation that relates trigonometric functions is a trigonometric function identity.
As we saw in Example
16, these identities
can also be extended
to coterminal angles.

All of the answer choices are sine functions. The graph begins at the midline when x = 0, like y = sin x, so this is a sine function shifted vertically downward.
The maximum of the graph shown is 1 and the minimum is −3. Let’s find their average.
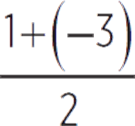 = −2/2 = −1
= −2/2 = −1
The midline is the line y = −1. The graph is shifted down 1 unit.
The amplitude is the difference between the midline value, −1, and the maximum, 1, or minimum, −3. So, the amplitude is 2.
Take a look at the period. This function has a period of 4π, so its period is twice that of the function y = sin x. The coefficient of x must be 1/2. So, the function must be y = −1 + 2 sin (1/2 x), which can also be written as y = −1 + 2 sin x/2. The correct answer is (C).
When squaring a trigonometric function, put the superscript immediately after the abbreviation. In other words, sin2 x = (sin x)2, or sin x ⋅ sin x.

Fully simplify the expression 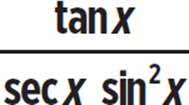 to find its equivalent trigonometric function, where the original expression exists.
to find its equivalent trigonometric function, where the original expression exists.
Use the basic trigonometric function identities and the rules of fractions to simplify the given expression.

This yields 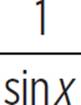 , and we can use a trigonometric identity to convert that to csc x.
, and we can use a trigonometric identity to convert that to csc x.
The expression 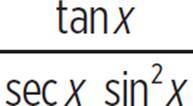 , where it exists, is equivalent to csc x.
, where it exists, is equivalent to csc x.

Let’s pause for a moment to consider the phrase “where it exists.” Recall from work in previous chapters that if any part of the original expression would be undefined—whether that’s from a denominator that’s equal to zero, or because a trigonometric function like tan π/2 doesn’t exist—then those values are not part of the solution set. That’s why it’s important that we include “where it exists,” so as to acknowledge any constraints on an equivalence.
Another useful trigonometric function identity is a version of the familiar Pythagorean identity.
As we learned earlier, the sine value of any central angle centered at the origin is the y-value of the point where its terminal side intersects the unit circle, and its cosine value is the x-value of that point.
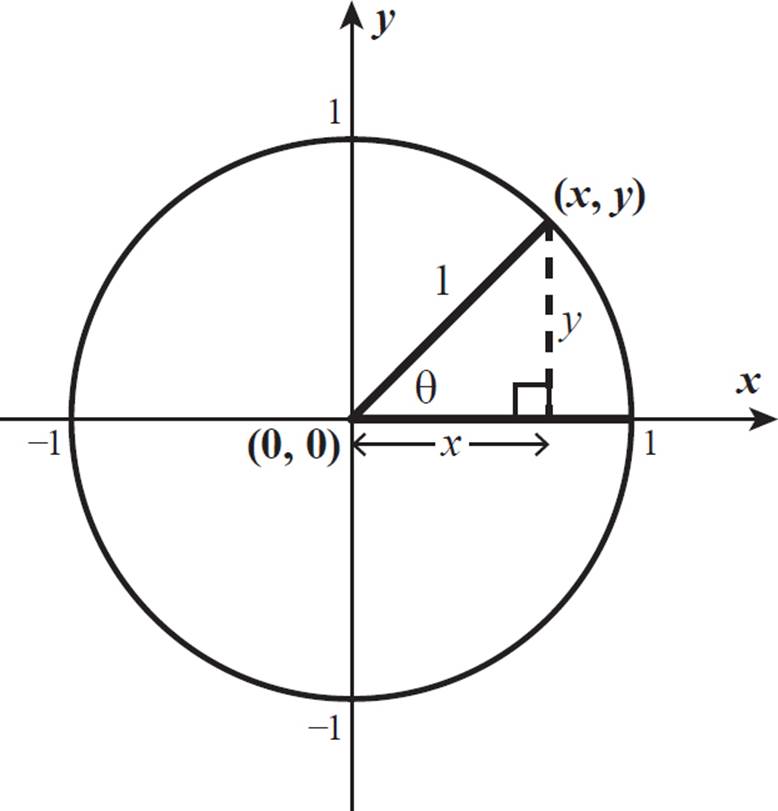
As shown in the diagram, the relationship between x, y, and 1 is a right triangle. By the Pythagorean theorem, x2 + y2 = 1. Even if the terminal side is in a different quadrant, where x and/or y is a negative number, the values still make the equation x2 + y2 = 1 true. Notice that this is the equation that describes the unit circle.

Here is how you may see the Pythagorean trigonometric identity on the ACT.
If 2x + sin2 θ + cos2 θ = 9, then x = ?
A. 1
B. 2
C. 3
D. 4
E. 5
Because x = cos θ and y = sin θ, the equation can be rewritten as cos2 θ + sin2 θ = 1, or, using the commutative property of addition, as sin2 θ + cos2 θ = 1.
The Pythagorean trigonometric identity states that sin2 θ + cos2 θ = 1 for any angle θ.
This identity allows you to solve for any trigonometric function value of an unknown angle if given the sine, cosine, or tangent of that angle and the quadrant in which it lies.

For an example of
how trigonometric
function identity
questions appear on
the ACT, please access
the online Student
Tools for this book.

For θ, an angle whose measure is between π/2 and π, cos θ = −3/5. What is sin θ? What is cot θ?
We are given the value of cos θ, −3/5. Substitute this into the Pythagorean trigonometric identity equation, sin2 θ + cos2 θ = 1.
|
sin2 θ + (−3/5)2 = 1 |
|
|
sin2 θ + 9/25 = 1 |
Evaluate the square. |
|
sin2 θ = 16/25 |
Subtract 9/25 from both sides, remembering that 1 = 25/25. |
|
sin θ = ± |
Take the square root of both sides. |
|
sin θ = ±4/5 |
Evaluate the square root. |
To determine whether sin θ is positive or negative, look at what quadrant its terminal side lies in. The measure of θ is given to be between π/2 and p, so the terminal side is in Quadrant II, where x-values are negative and y-values are positive. The sine is the y-value of the point where the terminal side meets the unit circle, so here sin θ is positive. The value of sin θ is 4/5.
Use one of the identities for cotangent to solve for cot θ.
|
cot θ = |
Use the identity that uses cosine and sine, since we know these values. |
|
cot θ = |
Substitute the values we found for cos θ and sin θ. |
|
cot θ = −3/5 ⋅ 5/4 |
Division by a fraction is multiplication by its reciprocal. |
|
cot θ = −3/4 |
Multiply, canceling out the common factor of 5. |
Solving the equation
sin2 θ + cos2 θ = 1 for sin
θ gives you sin θ =![]() .
.
Similarly, cos θ =![]() . You can
. You can
use these equations as
shortcuts when solving
for sin θ or cos θ. In
this case, we have sin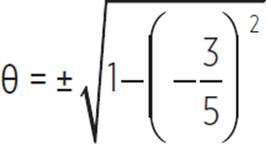 .
.
Remember that
the value that was
squared—in this case,
sin θ—could be either
positive or negative,
so include the ±
symbol when taking
the square root.

Another way to determine the sign of sin θ is by looking at the graph of y = sin x. When x is between π/2 and π, the value of sin x is always positive.
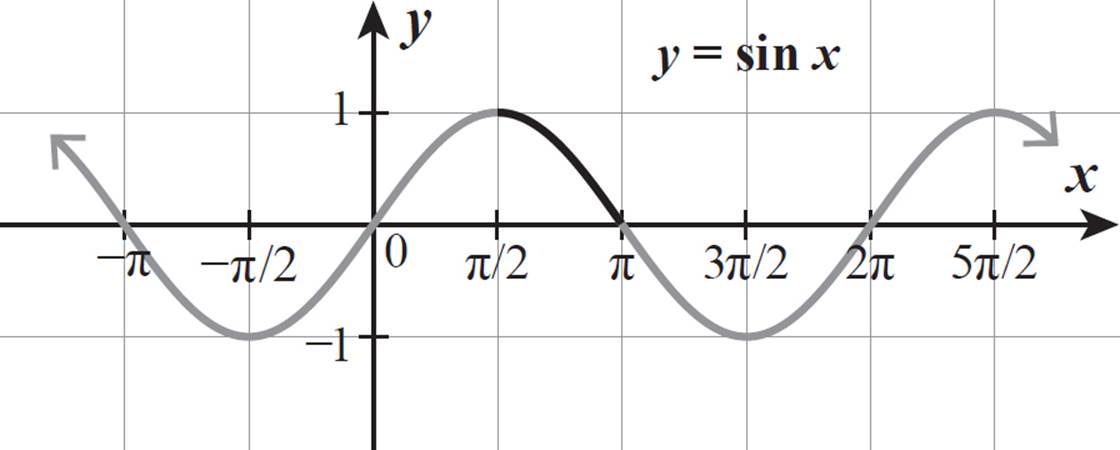
To solve for trigonometric function values of an unknown angle when given the tangent value of that angle and the quadrant of its terminal side, use the fact that tan θ = 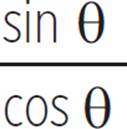 in conjunction with the Pythagorean trigonometric identity.
in conjunction with the Pythagorean trigonometric identity.

Use the fact that sin2 θ + cos2 θ = 1 for any angle θ.
|
2x + 1 = 9 |
Substitute 1 for sin2 θ + cos2 θ. |
|
2x = 8 |
Subtract 1 from both sides. |
|
x = 4 |
Divide both sides by 2. |
The correct answer is (D).

If tan θ = −8/15 and θ has a measure between 3π/2 and 2π, what is cos θ?
|
|
Substitute |
|
sin θ = −8/15 cos θ |
Multiply both sides by cos θ. |
Now that we have sin θ defined in terms of cos θ, let’s use the Pythagorean trigonometric identity.
|
sin2 θ + cos2 θ = 1 |
|
|
(−8/15 cos θ)2 + cos2 θ = 1 |
Substitute −8/15 cos θ for sin θ. |
|
64/225 cos2 θ + cos2 θ = 1 |
Square the entire expression (−8/15 cos θ). |
|
289/225 cos2 θ = 1 |
Combine the like terms on the left side of the equation. |
|
cos2 θ = 225/289 |
Multiply both sides of the equation by 225/289. |
|
cos θ = |
Take the square root of both sides. |
cos θ = ±15/17 Evaluate the square root.
The cosine of angles between 3π/2 and 2π is positive, so cos θ = 15/17.

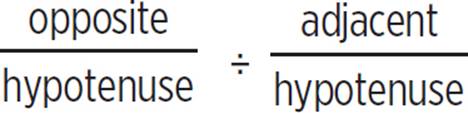
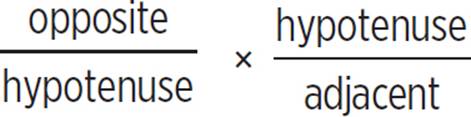
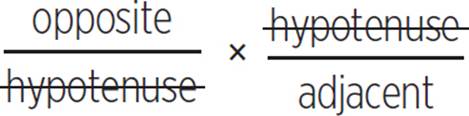
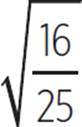
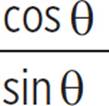
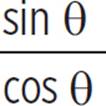 = −8/15
= −8/15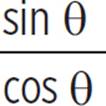 for tan θ in the given equation.
for tan θ in the given equation.