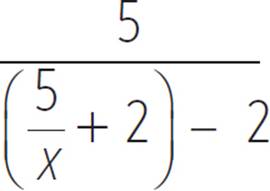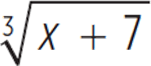High School Algebra II Unlocked (2016)
Chapter 5. Logarithms
GOALS
By the end of this chapter, you will be able to
•Find the inverse relation of a given function, including exponential functions, and determine any necessary domain restrictions on the function to make its inverse a function
•Evaluate or estimate numerical logarithms, where they exist
•Solve single-variable equations containing logarithmic expressions
•Use binary, natural, and common logarithms
•Use logarithmic identities
•Graph logarithmic functions
•Write and use logarithmic functions to represent real-life situations and solve problems
Lesson 5.1. Inverse Functions
REVIEW
A relation is set of ordered pairs, usually of the form (x, y), or an equation that describes a relationship between values in two sets. Functions are relations, but not all relations are functions.
Vertical line test: For a graph of a relation, if you can draw a vertical line somewhere that intersects the graph more than once, then the relation is not a function.
Switching x and y in a given relation reflects the graph of the relation across the line y = x.
A function maps each element in its domain (each x-value) to a single corresponding element in its range (a y-value, or f(x)-value). An inverse function takes every element in the original function’s range and maps it back to its corresponding element in the original function’s domain. So, the domain of a function is the range of its inverse function, and the range of a function is the domain of its inverse function.

For a refresher on
domains and ranges
you’ll want to refer
back to Lesson 3.3.
Inverse operations can
be found in Lesson 3.4.
In other words, an inverse function “undoes” or “reverses” whatever the original function did. In the simplest cases, an inverse function uses the inverse operation of the one used in the original function.
The functions f(x) = x − 8 and g(x) = x + 8 are inverse functions. The functions p(x) = x/3 and q(x) = 3x are also inverse functions. If you take an x-value in the domain of f(x), such as 10, the function f(x) produces the value 2. The inverse function, g(x), takes 2 and produces the value 10. The inverse function undid the work of f(x) and restored the original number. Likewise, p(x) takes an x-value of 12 and produces a p(x)-value of 4, while q(x) takes an x-value of 4 and produces a q(x)-value of 12.
When a function involves more than one operation, writing the inverse becomes a little more complicated. The idea is to create a new function that solves for each x-value from the original function’s domain, given its f(x)-value, or solving for x in terms of y. The only catch is that the old y-values must be the new domain values in the inverse function, meaning they must be x-values.
To find an inverse for a function, switch the x and y variables and solve for the new y in terms of the new x.
The notation f −1(x)
indicates the inverse
function of f(x). The
−1 is not an exponent,
so f −1(x) does not
mean [f(x)]−1.
This way, a coordinate pair (a, b) in the original function is reproduced as (b, a) in the inverse function.

If f(x) = 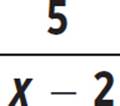 , what is f −1(x), its inverse?
, what is f −1(x), its inverse?
Use y in place of f(x), then switch the variables and solve for the new y.
|
y = |
Rewrite with y instead of f(x). |
|
x = |
Replace y with x and x with y. |
|
x(y − 2) = 5 |
Multiply both sides by (y − 2). |
|
xy − 2x = 5 |
Distribute the multiplication through the binomial factor. |
|
xy = 2x + 5 |
Add 2x to both sides. |
|
y = |
Divide both sides by x. |
|
y = 2 + 5/x |
Rewrite the fraction as two terms and simplify. |
The inverse function is f −1(x) = 5/x + 2.

Let’s try finding the composite function f −1(f(x)). A composite function is a function within a function. The outer function takes the output (function) values of the inner function and uses them as input values for its own function equation.
A composition of functions f(x) and g(x), specifically f composed with g of x, can be written as f(g(x)) or as (f ο g)(x). Likewise, g composed with f of x can be written as g(f(x)) or as (g ο f)(x).
In Example 1, f(x) = 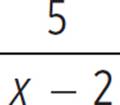 and f −1(x) = 5/x + 2. To write the composite function f −1(f(x)), replace f(x) with
and f −1(x) = 5/x + 2. To write the composite function f −1(f(x)), replace f(x) with 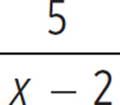 and then use that as x in the f −1(x) equation.
and then use that as x in the f −1(x) equation.
|
f −1(f(x)) |
= f −1 |
Substitute |
|
= |
Substitute |
|
|
= 5 · |
Rewrite division by |
|
|
= x − 2 + 2 |
Multiply and cancel out the common factor of 5. |
|
|
= x |
Add −2 and 2. |
So, f −1(f(x)) = x. This demonstrates that the inverse undoes the work of f(x), leaving us with each original element of the domain of f(x): each x-value.

Here is how you may see inverse functions on the ACT.
Given p(x) = 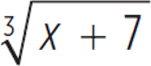 , which of the following expressions is equal to p−1(x) for all real numbers x ?
, which of the following expressions is equal to p−1(x) for all real numbers x ?
A. ![]() − 7
− 7
B. 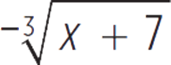
C. 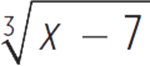
D. (x + 7)3
E. x3 − 7
What about function f composed with its inverse function, or f(f −1(x))?
|
f(f −1(x)) |
= f(5/x + 2) |
Substitute 5/x + 2 for f −1(x). |
|
= |
Substitute 5/x + 2 for x in the f(x) equation. |
|
|
= |
Combine 2 and −2 in the denominator. |
|
|
= 5 · |
Rewrite division by 5/x as multiplication by the reciprocal, x/5. |
|
|
= x |
Multiply and simplify. |
So, f(f −1(x)) is also equal to x. A function and its inverse undo one another. It works in either direction.
Functions f(x) and g(x) are inverses of one another if and only if f(g(x)) = x and g(f(x)) = x for all values of x in their domains.
Some functions have an inverse relation that is not a function. Sometimes a function maps more than one x-value to the same y-value. Its inverse relation must then map that one function value back to two different values, which means that it breaks the rules of function behavior.

Given y = x2 − 3, find its inverse relation, and graph both on the same coordinate grid.
Switch the variables x and y, and solve for the new y.
x = y2 − 3
y2 = x + 3
y = ±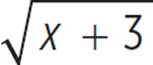
The inverse relation is y = ±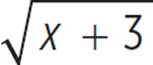 . This is not a function, because it produces both a positive and a negative number for each x-value (other than −3, which produces just 0). The graphs of y = x2 − 3 and y = ±
. This is not a function, because it produces both a positive and a negative number for each x-value (other than −3, which produces just 0). The graphs of y = x2 − 3 and y = ±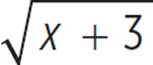 are shown on the coordinate grid below.
are shown on the coordinate grid below.
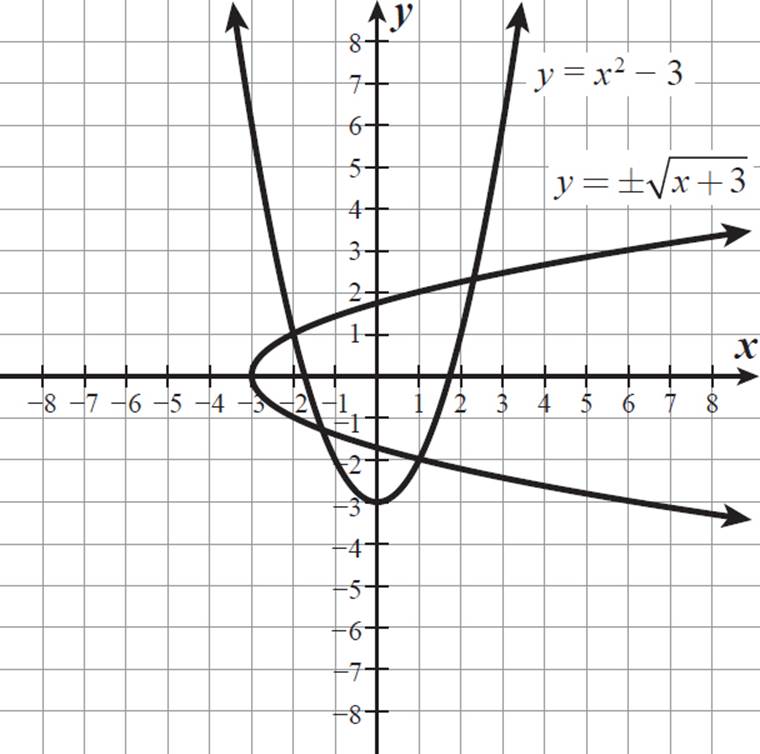
Notice that the graph
of y = ±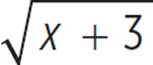
fails the vertical line
test for a function. A
vertical line can be
drawn that passes
through this graph in
more than one place.


|
y = |
Write using y instead of p(x). |
|
x = |
Switch x and y. |
|
x3 = y + 7 |
Cube both sides. |
|
x3 − 7 = y |
Subtract 7 from both sides to isolate y. |
So, p−1(x) = x3 − 7. The correct answer is (E).
Notice that, together, the two graphs are symmetrical with respect to the diagonal line y = x. This makes sense, because the way to reflect a graph across the line y = x is by switching the variables x and y in the given equation. We switched x and y in the equation y = x2 − 3, producing a relation (y = ±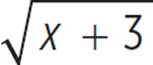 ) that is the reflection of the original function across the line y = x.
) that is the reflection of the original function across the line y = x.
Alternatively, we
could have restricted
the range of
y = ±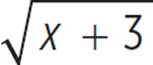 to only
to only
negative numbers
and 0. The functions
y = x2 − 3 for x ≤ 0
and y = −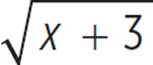 are
are
inverse functions.
Although y = ±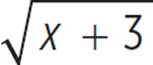 is not a function, if we include only the top half of its parabola, represented by the equation y =
is not a function, if we include only the top half of its parabola, represented by the equation y = 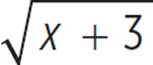 , then it becomes a function. In this case, though, only half of the function y = x2 − 3 is its inverse. We are restricting the range of the relation y = ±
, then it becomes a function. In this case, though, only half of the function y = x2 − 3 is its inverse. We are restricting the range of the relation y = ±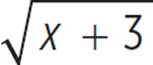 to only positive y-values and 0 (or y ≥ 0). The range of the inverse is the domain of the original function, so the domain of y = x2 − 3 must be restricted to only x ≥ 0. The inverse functions y= x2 − 3 for x ≥ 0 and y =
to only positive y-values and 0 (or y ≥ 0). The range of the inverse is the domain of the original function, so the domain of y = x2 − 3 must be restricted to only x ≥ 0. The inverse functions y= x2 − 3 for x ≥ 0 and y = 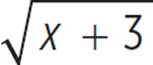 are shown on the graph below.
are shown on the graph below.
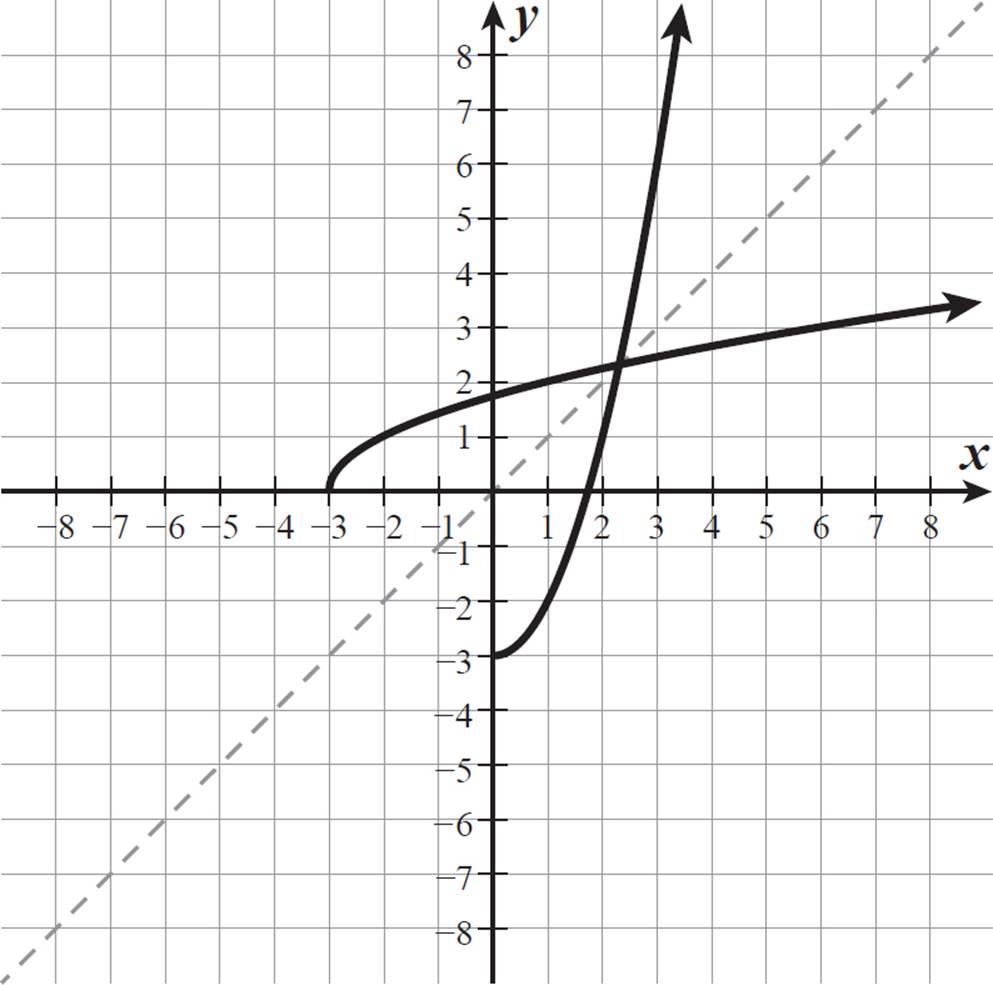
This graph also shows the line of reflection, y = x, as a dashed line.
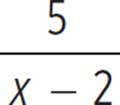
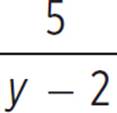
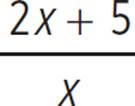
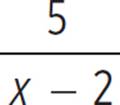 for f(x).
for f(x).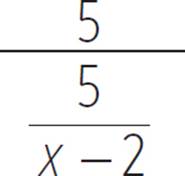 + 2
+ 2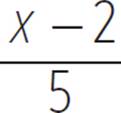 + 2
+ 2