High School Algebra II Unlocked (2016)

Lesson 1.2. Operations with Polynomials

REVIEW

Polynomials are terms or expressions that have one or more variables (raised to any whole-number exponent) and numbers. Monomials have one term, binomials have two, and trinomials have three.

As with complex numbers, the commutative, associative, and distributive properties apply to polynomials. Use these properties, as well as the properties of exponents, to perform operations on polynomials. Always fully simplify your answer.

Expand and simplify: (x − 5)(x² + 3x − 4)

We can use the distributive property to rewrite the product as the sum of the product of x and the trinomial and the product of −5 and the trinomial.

A subtraction of 5 is the
same as an addition of
−5. The negative sign
needs to be included in
the multiplication of each
term in the trinomial: (−5)
(x²) + (−5)(3x) + (−5)(−4).

A real number can be
described as a monomial
in which the only x-term
has an exponent of 0.
Remember, a polynomial
includes at least one
variable raised to any
whole-number exponent,
and 0 is a whole number.
The value of x⁰ is 1,
so the number 8 is
the polynomial 8x⁰.

In this example, the product of two polynomials is another polynomial. In fact, whenever you add, subtract, or multiply polynomials, the result will always be another polynomial. We say that polynomials are closed under the operations of addition, subtraction, and multiplication. Even in the case of (x + 6) + (−x + 2), the sum, 8, is still a polynomial. All real numbers are polynomials.

Integers, like polynomials, are closed under addition, subtraction, and multiplication. Notice that neither integers nor polynomials are closed under division. If you divide an integer by another integer, you may end up with a non-integer such as 3/4. If you divide a polynomial by another polynomial, you may end up with a non-polynomial such as 5/x or x⁻².

Uta has designed a vase that is cylindrical but has a solid glass hemispherical base, as shown below.

Write a formula for the volume capacity of the vase, in terms of r, the radius of its circular base, and h, its height. Then, rewrite the formula according to a rule that the height of the vase must be 3 inches greater than the diameter of the vase.

The capacity of the vase is the total capacity of a cylinder this size (πr²h) minus the volume of the hemispherical base. A hemisphere is half of a sphere, so the volume of this hemisphere is 1/2 (4/3πr³), or 2/3 πr³. Let’s translate this information into an equation: The capacity of the vase is given by the formula V = πr²h − 2/3 πr³.

Remember, the volume
of a cylinder is given by
the formula V = πr²h,
and the volume of a
sphere is given by the
formula V = 4/3 πr³.

Here is how you may see operations with polynomials on the ACT.

The expression (n² − 8n + 1)(n + 3) is equivalent to:

A. n³ − 8n² − 24n + 3

B. n³ − 7n² − 21n + 3

C. n³ − 5n² + n + 3

D. n³ − 8n² + n + 3

E. n³ − 5n² − 23n + 3

If the height must be 3 inches greater than the diameter, then h = d + 3. The diameter is twice the length of the radius (d = 2r), so h = 2r + 3. Let’s substitute this expression in terms of the radius for height in our volume formula.

Keep an eye out for
questions that ask
for a specific unit of
measurement. This
formula gives volume
in cubic inches, not
capacity in ounces or
liters, since h was defined
in terms of inches.

V = πr²(2r + 3) − 2/3 πr³

Expand and combine like terms to simplify.

V = 2πr³ + 3πr² − 2/3 πr³

V = (2πr³ − 2/3 πr³) + 3πr²

V = πr³(2 − 2/3) + 3πr²

V = πr³(4/3) + 3πr²

V = 4/3 πr³ + 3πr²

We can also use our polynomial operation skills to uncover the pattern behind raising a binomial to various whole-number exponents.

Expand (x + y)¹, (x + y)², (x + y)³, and (x + y)⁴.

(x + y)¹ = x + y
(x + y)² = (x + y)(x + y) = x(x + y) + y(x + y) = x² + xy + xy + y² = x² + 2xy + y²

Let’s rewrite (x + y)³ as (x + y)(x + y)² then substitute the expression we found for (x + y)².

Let’s rewrite (x + y)⁴ as (x + y)(x + y)³ then substitute the expression we found for (x + y)³.

Do you see a pattern? Each expanded expression begins with x raised to the power that (x + y) was raised to, and each ends with y raised to that power. In each consecutive term within the expanded expression, the power of xdecreases by 1 and the power of y increases by 1.

The coefficients of the terms also seem to follow a pattern: (1, 1), (1, 2, 1), (1, 3, 3, 1), and (1, 4, 6, 4, 1). Each set of coefficients is like a palindrome. Even more interesting, they follow the pattern of numbers shown in the triangle below. This pattern was discovered by Blaise Pascal and is now referred to as Pascal’s Triangle.

The 1 in the first row
represents (x + y)⁰, which
is equal to 1, because any
non-zero number raised
to a power of 0 is equal to
1. Then, as you saw from
Example 8, the second
row shows the coefficients
for (x + y)¹, the third row
shows the coefficients
for (x + y)², and so on.

The triangle continues infinitely beyond what is shown here, with an expanding base. Each number is the sum of the two numbers in the row above it immediately to the left and right of its placement.

The Binomial Theorem states this pattern formally with the equation

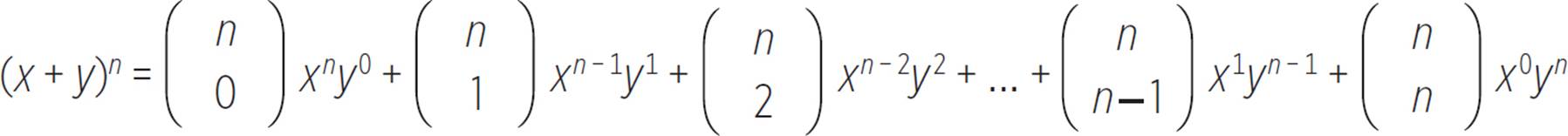
where each 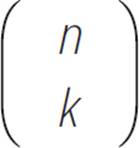is the binomial coefficient, as shown in Pascal’s Triangle.

We can use the distributive property to rewrite the product as the sum of the product of n and the trinomial and the product of 3 and the trinomial.

Expand (a² − 2ab)⁵.

First, rewrite the binomial as a sum, to fit the form for the Binomial Theorem: [a² + (−2ab)]⁵.

The binomial is raised to a power of 5, so the coefficients we need are in the 6th row of Pascal’s Triangle: 1, 5, 10, 10, 5, and 1.

To expand a binomial
raised to the n th power,
use the numbers from row
(n + 1) of Pascal’s Triangle
as the coefficients.