High School Algebra II Unlocked (2016)
Chapter 7. Making and Using Mathematical Models
GOALS
By the end of this chapter, you will be able to:
•Manipulate given equations to solve for certain variables or to reveal properties of functions
•Determine key features of functions from equations, tables, and graphs, and interpret those features in the context of the situations described by the functions
•Model described situations with equations and inequalities, and use them to solve problems
•Model described situations with graphs, and use them to solve problems
Lesson 7.1. Manipulating Equations
Many relationships in the world around us can be modeled using math, in the form of equations, inequalities, and graphs. When we are given a representative equation, we may be able to manipulate it to make better use of it.
For example, if we have the formula that converts temperatures in degrees Celsius (variable C) to degrees Fahrenheit (variable F), F = 9/5 C + 32, then we can rewrite this equation to perform conversions in the other direction. Solve forC, using the same algebraic solution methods that you would use to solve a single-variable equation, treating F as just another number.
|
F = 9/5 C + 32 |
|
|
F − 32 = 9/5 C |
Subtract 32 from both sides. |
|
5/9 (F − 32) = C |
Multiply both sides by 5/9, the reciprocal of 9/5. |
Now we have the formula C = 5/9 (F − 32), which can be used to directly convert temperatures in degrees Fahrenheit to degrees Celsius.

Here is how you may see manipulation of equations on the ACT.
Oliver discovers that the current value of his car can be calculated using the equation x = P(1 − d)n, where x is the current value, P is the original price Oliver paid for the car, d is a depreciation constant for that kind of car, and n is the number of years since he bought it. Which of the following is an expression for d in terms of P, n, and x?
A. 1 − 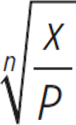
B. 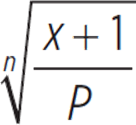
C. ![]()
D. 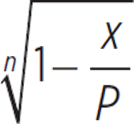
E. 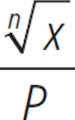 + 1
+ 1

If a car accelerates at a steady rate, then the distance, d, the car travels in time, t, is given by the formula d = vit + 1/2 at2, where vi is the car’s initial velocity and a is its acceleration. Write a formula that gives a in terms of vi and t. Then, use the fact that the rate of acceleration is the ratio of the change in velocity (from the car’s initial velocity to its final velocity, vf) to the change in time, to write a formula for vf in terms of d, t, and vi.
First, we must solve the given equation for a.
|
d = vit + 1/2 at2 |
|
|
d − vit = 1/2 at2 |
Subtract vit from both sides. |
|
2(d − vit) = at2 |
Multiply both sides by 2. |
|
|
Divide both sides by t2. |
The formula for acceleration is a = 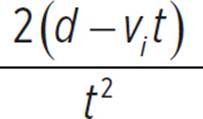 , which can also be written as a =
, which can also be written as a = 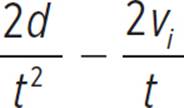 .
.
The fraction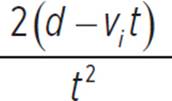 can be
can be
written as 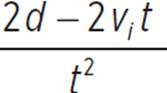
and then broken
into the sum of two
fractions with the
same denominator: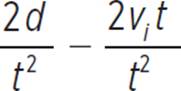 . By
. By
canceling out a factor
of t in the numerator
and denominator of
the second fraction,
we get 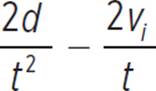 .
.
The acceleration rate is the change in velocity over the change in time. The variable t represents the time that the car has been moving distance d, so the change in time is just t. The change in velocity is vf − vi.
a = 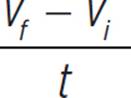
Let’s substitute this expression for a into our formula.
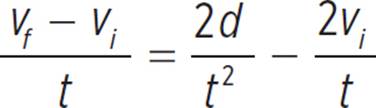
Now we can solve for vf.
|
vf − vi = t |
Multiply both sides by t. |
|
vf − vi = |
Distribute the factor of t to both terms in the parentheses. |
|
vf = |
Add vi to both sides. |
This formula gives vf in terms of d, t, and vi.

Sometimes, instead of solving for a different variable, you just need to rearrange a given equation to reveal various properties of the function. For example, in Chapter 1, Example 13, we rearranged the given function h = −16t2 + 48t + 64 in factored form as h = = −16(t + 1)(t − 4) to find its x-intercepts (t-intercepts), −1 and 4, and in vertex form as h = −16(t − 3/2)2 + 100 to find its vertex, (3/2, 100).

To graph the function y = 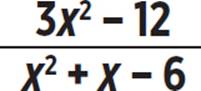 , Bonnie wants to determine the horizontal asymptote, the vertical asymptote, and any holes in the graph. Which of these can she best assess from the current form of the function? Rewrite the function to reveal the other two properties.
, Bonnie wants to determine the horizontal asymptote, the vertical asymptote, and any holes in the graph. Which of these can she best assess from the current form of the function? Rewrite the function to reveal the other two properties.
When the numerator and denominator of a rational function are of the same degree, as they are here, the horizontal asymptote is the line y =  . So, in this form, Bonnie can easily see that the function has a horizontal asymptote at y= 3/1, or y = 3.
. So, in this form, Bonnie can easily see that the function has a horizontal asymptote at y= 3/1, or y = 3.
To determine the vertical asymptote and any holes in the function, she must factor both the numerator and the denominator.
|
y = |
Factor 3 out of the numerator. |
|
y = |
Factor the quadratics in the numerator and denominator. |
Any zero of the denominator represents a point of discontinuity in the function. If the zero is also a zero of the numerator, then the discontinuity is a hole. If the zero is not a zero of the numerator, then the discontinuity is a vertical asymptote. This function has a hole when x = 2 and a vertical asymptote of x = −3.
The factored form of
the rational function
also tells you that
the function has an
x-intercept of −2,
because that value will
make the factor (x + 2)
of the numerator equal
to 0 (but will not make
the denominator 0).


|
x = P(1 − d)n |
|
|
x/P = (1 − d)n |
Divide both sides by P. |
|
|
Take the nth root of both sides. |
|
|
Subtract 1 from both sides. |
|
− |
Multiply both sides by −1. |
|
1 − |
Use the commutative property of addition. |
The correct answer is (A).
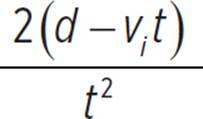 = a
= a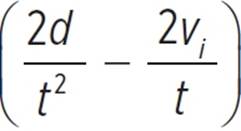
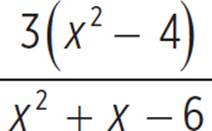
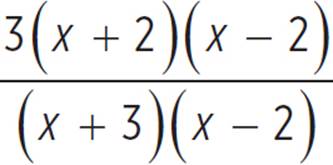
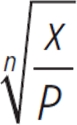 = 1 − d
= 1 − d