Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 3. Limits and Continuity

TECHNOLOGY: EVALUATING LIMITS WITH A GRAPHING CALCULATOR

You can sum up the whole concept of limits in one statement: A limit is a height toward which a function is heading at a certain x value. With this in mind, a graphing calculator greatly simplifies the limit process. Many times, the function you are given is bizarre looking, and its graph is beyond the grasp of mere mortal men and women in the time allotted to answer an AP question. The majority of these limit questions appear on the non-calculator portion of the AP test, forcing you to use the substitution, factoring, and conjugate methods to reach an answer. However, evaluating limit problems will sometimes seep into the calculator-active section like a viscous, sticky goo. In these cases, limits are no match for you at all, as the calculator affords you numerous tools in your dual quests for a 5 on the AP test and peace in the universe.

ALERT! Remember that your calculator can only be used to approximate limits. Using the calculator to approximate a limit may not be acceptable on a free-response question. This method is only your last resort!

Example 12: Evaluate using your calculator.

Solution: You solved this problem in an earlier exercise using the conjugate method (which works just fine) and got —1/6. Graph it on your calculator—it looks almost like a straight line (but it’s definitely not linear).

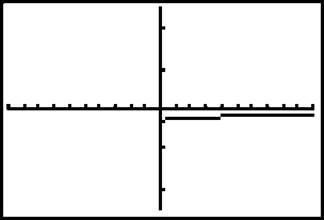
Use the [2^nd] → [Trace] → “value” command on your calculator to find the value of the function at x = 9. The corresponding y value should come out blank! This makes sense, because 9 is not in the domain of the function. Therefore, substitution does not work. However, we can use the calculator to substitute a number very close to 9. This value is a good approximation of the limit for which you are looking. Again, use the [2^nd] → [Trace] → “value” function of your calculator to evaluate the function at x = 8.9999.

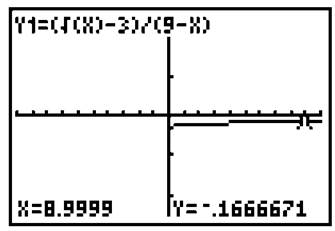
The calculator gives a limit of x = —.1666671. Using other x values even closer to 9 (e.g., 8.99999999999), the approximation looks more like —.16666666667, which is approximately —1/6, the exact value we received from using the conjugate method.

Example 13: Show that using your calculator.

Solution: Using the rule for rational functions at infinity, the limit is clearly 3/5 as the degrees of the numerator and denominator are the same. The graph certainly appears to approach that height as x approaches both ∞ and —∞.

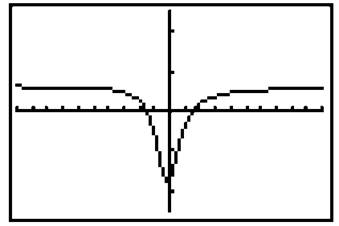
To verify this numerically, press [Trace] and repeatedly press the right arrow key. The function’s height will slowly get closer to 3/5 = .6.

Another option open to you is the [2^nd] → graph (or [Table]) function of the calculator, which lists function values quickly.

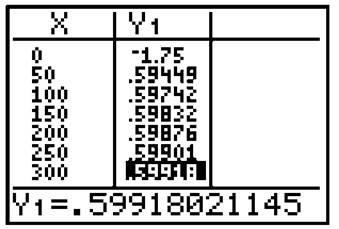
Clearly, the function approaches a limiting height of .6 as x approaches ∞.

EXERCISE 8

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

1. If exists, what must be true?

2. Given 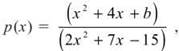find the value of b that ensures p is nonremovably discontinuous only once on (—∞,∞).

3. What conditions must be met if f(x) is continuous at x = c?

4.

5. Design two functions, g(x) and h(x), such that g(x) + h(x) = 4x² + 3x + 1 and

6. What three function behaviors prevent a limit from existing?

7. What value of a makes k continuous if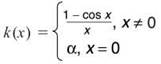

8.

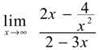
9. If d(x) is defined by the graph below, answer the following questions:

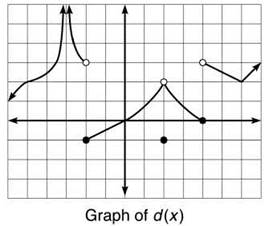
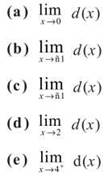
(f) List all x values where d is discontinuous.

(g) Which of your answers to part (f) represents removable discontinuities, and why?

(h) What value(s) of β make the following statement true?

10.

11. Give the equations of the horizontal and vertical asymptotes of if a and b are real numbers.

12.

13. The population, v, of the bacteria Makeyoucoughus hurtyourthroatus is modeled by the equation y = 50e^.1013663t, where t is days and y is the number of colonies of bacteria. Use the Intermediate Value Theorem to verify that the bacteria will reach a population of 100 colonies on the time interval [4,7].

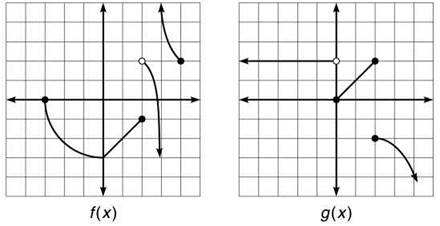
14. If f(x) and g(x) are defined by the graphs below, evaluate the following limits (if possible):

15. Find the values of c and d that make m (x) continuous if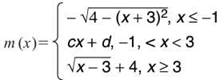

16. James’ Diabolical Challenge Problem:

Given 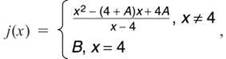j(2) = 1 and j(x) is everywhere continuous, find A and B.

ANSWERS AND EXPLANATIONS

1. The three conditions for a limit to exist are: (1) exists, (2) exists, and (3) they are equal.

2. The denominator of p factors to (2x — 3)(x + 5), so p will be discontinuous at x = 3/2 and —5. If the numerator contains one of these factors, our goal will be achieved. It makes good sense to force (x + 5) to be a factor, rather than (2x — 3) because the leading coefficient of the numerator is 1. (In other words, the numerator will factor into (x + A)(x + B) and (x + 5) is of this form.) To find b, we factor the numerator using (x + 5) as one of the factors:

Subtract x² from each side and factor to get

Thus, 5+^1 (the coefficient of x on the left side of the equation) must equal 4 (the coefficient of x on the right side of the equation).

Therefore, (x — 1) is the remaining factor. Thus,

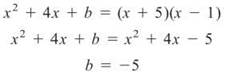
Because (x + 5) is a factor of the numerator and denominator, exists, and the discontinuity there is removable. The discontinuity at x = 3/2 has no limit because which indicates a vertical asymptote (essential discontinuity).

3. If f(x) is continuous at x = c, then (1) exists, (2) f(c) exists, and (3) the two are equal.

4. Multiply the binomials in the numerator to get Because this is a rational function evaluated at infinity, you can use the shortcut method of examining their degrees. Because the degree of the denominator exceeds the degree of the numerator, the function’s limit at infinity is 0. Don’t be confused because x→ —∞. Remember that a rational function approaches the same limits as x→∞ and —∞.

5. Because is a rational function and we know that the leading coefficients of g(x) and h(x) must be in the ratio 3:1. One possible g(x) is 3x² + 2x + 1. The matching h(x) would have to be x² + x. Notice that the sum of the two functions is 4x² + 3x + 1, as directed, and There are numerous possible answers, but they will work in essentially the same fashion.

6. If a function oscillates infinitely, increases or decreases without bound, or has right- and left-hand limits that are unequal, the function will not possess a limit there.

7. Special Limit Rule 4 gives us that Thus, and the first condition of continuity is met. Notice that k(0) = α, and (for k to be continuous) a must equal that limit as x approaches 0. Therefore, α = 0.

8. Use Special Limit Rule 1 to simplify the fraction as follows:

This is a rational function being evaluated at infinity with equal degrees in the numerator and denominator, so the limit is equal to

9. (a) 0

(b) -1: Remember the key is that you are approaching —1 from the right, not to the right.

(c) 3

(d) 2: even though f(2) = —1, the function leads up to a height of 2 when x = 2

(e) 3

(f) x = —3, —2,2,4

(g) x = 2: If you redefine d such that d(2) = 2 (instead of —1), then the limit and the function value are equal to 2 and d is continuous there. No other discontinuities can be eliminated by redefining a finite number of points.

(h) β = —3,∞: d increases without bound as you approach 3 from the left and the right; the graph also increases without bound as x approaches ∞.

10. You don’t have to use special limit rules here—substitution is possible. The answer is sin 2/2, or .455.

11. Factor the fraction fully to get

The denominator of g will equal 0 when However, the numerator will not equal zero simultaneously. Thus, vertical asymptotes are present, and the equations for the vertical asymptotes are x = —b/3a and x = b/2a. To find the horizontal asymptotes, note that the numerator and denominator have the same degree, and find the limit at infinity.

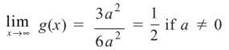
From this, you know that the horizontal asymptote is y = 1/2.

12. It’s the revenge of the conjugate method! Multiply the numerator and denominator of the fraction by the conjugate of the expression.

Because the degrees of the numerator and denominator are both 1 (since √x² = x), you find the limit by taking the coefficients of the terms of that degree and ignoring the rest of the problem (just as you’ve done in the past with rational limits at infinity).

13. The population at t = 4 is approximately 75, and the population at t = 7 is approximately 101.655. The Intermediate Value Theorem guarantees the existence of a c ∈ [4,7] such that f(c) = 100.

14. (a) No limit: does not exist, so f(x) — 3 g(x) cannot have a limit.

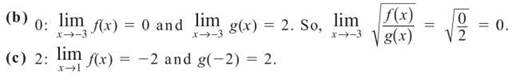
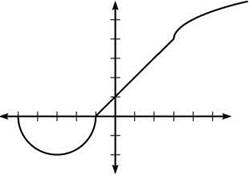
15. The graph will begin as a semicircle of radius 2 centered at (—3,0), will become a line (since cx + d is linear) between the x values of —1 and 3, and will end as the graph of √x shifted to the right 3 and up 4. To find the first point on the linear section, plug —1 into the first rule: The line will begin at point (—1,0). The line will end at The focus of the problem, then, is to find the equation of the line that passes through (—1,0) and (3,4). Find the slope of the line and use point-slope form to get

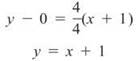
Therefore, the correct c and d values are both 1. The solution is further justified by the graph of m.

16. To begin, factor the function and use the fact that j(2) = 1.

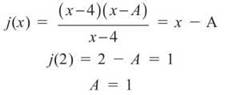
Since the function is continuous, must be equal to f(4). So, you get f(4) = 4 — 1 = B (according to the given information); B = 3.

SUMMING IT UP

• Remember that the limit of a graph at x = c is the height that the graph reaches at x = c.

• Limits answer the question “Where is a function heading?”

• Only point discontinuities are removable, because a limit exists.

• Rational, polynomial, radical, exponential trigonometric, and logarithmic functions are always continuous at all points in their domain. To help remember this, use the mnemonic device

• Red Parrots continuously Repeat Everything They Learn.