Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 4. Differentiating
THE POWER RULE
Many years ago, I attended a F aye Kellerman book signing with my father in California. The famous mystery writer politely asked what I did for a living as I handed her a copy of her most recent book, Prayers for the Dead, to sign for me. When she found out I was a calculus teacher, she confessed to taking many math classes in college and that one of the most vivid things she remembered from calculus was how to take a derivative with the power rule. This sentiment is echoed by many of the people I meet—but only by those who will maintain eye contact with me when they find out I am a math teacher.
The Power Rule is the most basic of derivative techniques, used when you encounter a variable raised to a constant power:
The Power Rule: If y = xc, where c is a real number, then y' = c ∙ xc-1
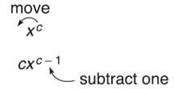
TIP. Visually, you “pull the exponent down” in front of the variable and subtract one from the power.
The Power Rule, so named because the variable is raised to a power, also works if a coefficient is present. In the case of y = nxc, you still bring the original exponent c to the front and subtract one from the power, but now the c you brought to the front gets multiplied by the n that was already there. For example, if y = 5x4, then by the Power Rule, y' = 5 ∙ 4x3 = 20x3.
That’s the Power Rule in its entirety. Sometimes, the Power Rule will apply even though it is not obvious—some rewriting will be necessary first, as demonstrated below.
ALERT! The derivative of y = 2x is not y' = x ∙ 2x-1. The Power Rule works only when a single, solitary variable is raised to a constant power.
Example 4: Use the Power Rule to find the derivative of each of the following:
(a) y = x8
This is a straightforward example: y’ = 8x7.
(b) f(x) = 2x3 + 9x2
ALERT! You cannot find the derivatives of products or quotients as easily as you did in 4(b). Unlike sums and differences, they have special rules (the Product and Quotient Rules) that govern their derivatives.
This problem is a sum, so each term can be differentiated separately—the same would be true for a difference. Remember, when you “bring down” the powers, you need to multiply by the coefficients that are already present.
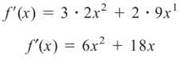
c) y = 5/x2
Rewrite this as 5x-2 to apply the Power Rule:
TIP. Even though you can find the derivatives of 4(e) and 4(f) using the Power Rule, it’s better if you can find the derivatives immediately using the important facts listed there.
d) 
This fraction can be simplified to 
so 
(e) y = 6
You can rewrite this as y = 6x0, since x0 = 1 (as long as x ≠ 0, but don’t worry about that). If y = 6x0, then y' = 0 ∙ 6x-1 = 0. This is an important fact: The derivative of any constant term is zero.
(f) y = 7x + 5
This is the same as 7x1, so y' = 1 ∙ 7x0 = 7 ∙ x0 = 7 ∙ 1 = 7. This is another important fact: The derivative of a linear polynomial, y = ax + b, is a.
Now that you have some practice under your belt, try some slightly trickier problems in Example 5. More rewriting is required here in order to apply the Power Rule.
Example 5: Find dy/dx for each of the following:
(a) y = (x2 - 1)(x + 5)
You’ll have to multiply these binomials together before you can apply the Power Rule. You cannot simply find the derivative of each factor and then multiply those. Remember, products and quotients have their own special rules, and we haven’t gotten to those yet.
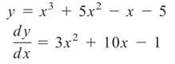
b) y = (2x3)2
NOTE. The directions in Examples 1 through 5 ask you to find the derivative but in different ways. Be able to recognize different kinds of notation. More on the notation d/dx and dy/dx in the section entitled “A Word About Respecting Variables.”
Square the (2x3) term first to get y = 4x6. Clearly, then, 
(c) 
Some rewriting and distributing is necessary to begin this problem:
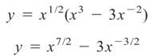
Now the Power Rule applies:
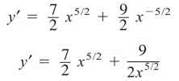
EXERCISE 2
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
DO NOT USE A GRAPHING CALCULATOR FOR ANY OF THESE PROBLEMS.
1. Find dy/dx if y = 12xπ.
2. If f(x) = x4 + 3x2 — 1, what is f’(x)?
3. Calculate 
4. Find DX [2x - 1]3.
5. Find y’ if 
6. What is the equation of the tangent line to h(x) = 2x3 — 3x + 5 at the point (1,4)?
7. How many derivatives must you take of g(x) = 4x2 + 9x + 6 until you get zero?
ANSWERS AND EXPLANATIONS
1. π is just a real number, so you can still apply the Power Rule: 
2. Each of the terms can be differentiated separately, so f'(x) = 4x3 + 6x. Don’t forget that the derivative of any constant (in this case 1) will be 0.
3. Rewrite the expression to get 
or 
The 1/4 is now a constant and we can apply the Power Rule. The derivative will be 
4. A common mistake is to assume that the derivative is 3(2x — 1)2. This is not correct. Instead, expand the expression before applying the Power Rule:
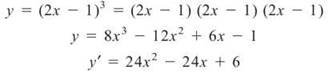
5. This one is a little ugly to start with. Some rewriting and distributing will fix that:
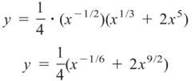
Notice that the 4 in the denominator squirts out easily to become the coefficient 1/4. This is not absolutely necessary, but it simplifies your calculations. As in past examples, leave the coefficient alone until the last step and then multiply it through:
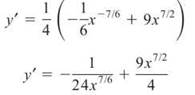
NOTE. The second derivative of f(x) can be written as f"(x) or 
Similarly, the third derivative can be written as f"'(x) or 
6. To create the equation of a line, you need a point and a slope; point-slope form will then easily follow. You are given the point (1,4), and the slope of a tangent line may be found by the derivative. Thus, the slope we need is given by h'(1):
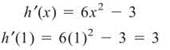
Apply the point-slope formula using m = 3 and (x1,y1) = (1,4):
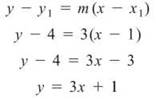
7. Each of the derivatives is pretty easy: g'(x) = 8x + 9, g"(x) = 8, g"'(x) = 0. The third derivative, then, will give you zero.