Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 4. Differentiating
DERIVATIVES TO MEMORIZE
Before exploring other tools of differentiation, it is necessary to supplement your toolbox. If the Power Rule is the hammer of derivatives, it is pretty useless without a collection of different kinds of nails—one for every purpose. Calculus is full of derivatives, most of which cannot be nailed down by the Power Rule alone. In order to succeed in calculus and on the AP test, you’ll need to be able to derive the functions in this section automatically, without even a second thought. In other words, memorize, memorize, memorize. Although memorizing may not be a glorious road to enlightenment, it has plenty of clean rest stops along the way with reasonably priced vending machines.
Trigonometric Derivatives
Trigonometric functions and their derivatives are all over the AP test. By not memorizing these, you are crippling yourself and your chance to score well.
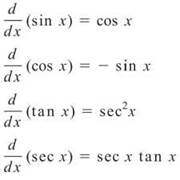
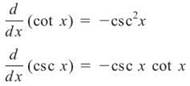
NOTE. The notation for each derivative formula is d/dx, which means the derivative with respect to x.
Note the similarities between the tangent and cotangent functions as well as the cosecant and secant functions. It is also important to note that all the co-trigonometric derivatives are negative.
Logarithmic Derivatives
In traditional courses, logarithmic and exponential derivatives are not introduced until the end of calculus. However, this is not the case any more. In fact, the functions are pervasive on the AP test, so it is common practice now to introduce them right away. The result is a lot more to memorize at first, but greater success and mastery later.
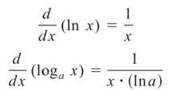
You will see far more natural logs on the AP test, but logs with different bases occasionally make cameo appearances.
NOTE. The a in the logarithmic and exponential derivative formulas represents a constant.
Example 6: Find f'(t) if f(t) = 4log3 t.
Solution: Remember, when finding derivatives, you can ignore the coefficient and multiply through at the end. Therefore, according to the formula,
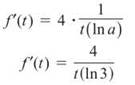
Exponential Derivatives
It doesn’t get much easier than exponential derivatives, especially ex.
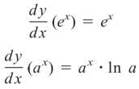
Notice that the derivative of ax involves multiplying by the natural log of the base used. This is similar to deriving logax, in which you divide by the natural log of the base used. This makes sense, because exponential functions and logarithmic functions are inverse functions, just like multiplication and division are inverse operations.
Example 7: Find y' if y = esc x — lnx + 5x without consulting your derivative formulas.
Solution: If you are memorizing these formulas as you proceed, this problem is relatively simple: ![]()
Inverse Trigonometric Function Derivatives
TIP. If anyone told you that there was no memorizing in calculus, they were lying to you.
These functions revisit you later, during the integration section of the book. Knowing them now makes life so much easier down the road. Some textbooks use the notation sin-1x to denote the inverse sine function, whereas many use arcsin x. Both mean the same thing. I personally prefer arcsin x because sin-1x looks hauntingly similar to (sin x)-1, or csc x.

Things start getting messy with arcsecant, but all these derivatives have things in common. Notice that the derivatives contain (1 + x2), ![]() and
and ![]() Learning which denominator goes with which inverse function is the key to recognizing these later. Also note that the co- derivatives are again negative, as they were with ordinary trigonometric function derivatives.
Learning which denominator goes with which inverse function is the key to recognizing these later. Also note that the co- derivatives are again negative, as they were with ordinary trigonometric function derivatives.
EXERCISE 3
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
DO NOT USE A GRAPHING CALCULATOR FOR ANY OF THESE PROBLEMS.
1. Below is a list of all the functions whose derivatives were listed in this section. Complete the table without the use of notes.
Note: You may want to make a few photocopies of this problem and complete them every few weeks to keep the formulas fresh in your mind.

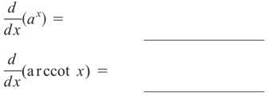
2. Name each function whose derivative appears below:
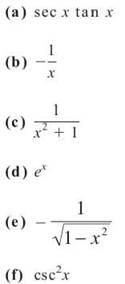
3. Find each of the following derivatives:
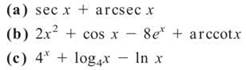
4. Name a function, g(x), other than ex such that g'(x) = g(x).
ANSWERS AND EXPLANATIONS
1. Check answers with the formulas listed previously in this section.
2. (a) sec x
(b) —ln x: The —1 is a coefficient, so ![]()
(c) arctan x: By the commutative property of addition, 1 + x2 = x2 + 1
(d) ex
(e) arccos x
(f) —cot x: By the same reasoning as 2(b) above.
3.
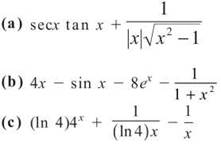
4. The easiest such function is g(x) = 0, since the derivative of any constant is 0.