Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 4. Differentiating
THE QUOTIENT RULE
Just like products, quotients of functions require their own special method of differentiation. Because multiplication and division are so closely related, you can use the Product Rule to develop the Quotient Rule from scratch. In Example 12, your objective will be to create the Quotient Rule.
TIP. The words top and bottom refer to the fraction’s numerator and denominator, respectively. If you refer to the numerator of a fraction as the top during math class, your teacher may hit you in the mouth with a hard leather shoe.
Example 12: Use the Product Rule to find the derivative of 
Solution: You must rewrite the quotient as a product before you can begin: y = f(x) ∙ (g(x))-1. Now, apply the Product Rule and simplify completely.
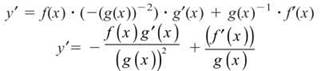
Multiply the second term by 
to get common denominators and then combine the terms.
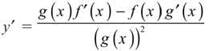
The Quotient Rule: If 
then 
Translation: If a fraction is formed by two functions, the derivative is found by multiplying the bottom by the derivative of the top minus the top times the derivative of the bottom, all divided by the bottom squared. Some people use the following verbal device to remember the Quotient Rule:
Example 13: Find p'(t) if 
Solution: Applying the Quotient Rule, the derivative is as follows:
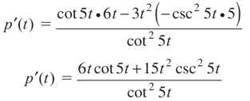
ALERT! There are all kinds of ways to screw up the Quotient Rule. Often, people concentrate so hard on getting the numerator of the Quotient Rule correct, they forget to write the denominator. Don’t forget to square your bottom!
Example 14: Find h'(e) if 
Solution: This problem begins with the Product Rule.
Finding the derivative of 
will require the Quotient and Chain Rules.
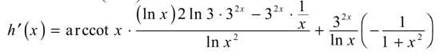
That sure isn’t pretty. Now find h'(<?), and remember that ln e = 1. That will remove some of the grime.
You can find the decimal value of this load using your calculator, but why put yourself through that much agony? If you do a single thing wrong when entering it into your calculator, you could lose those points you earned the hard way; be a heads-up test taker—if simplifying isn’t worth it, leave the answer unsimplified.
EXERCISE 6
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE YOUR CALCULATOR ONLY FOR PROBLEM 4.
1. Find f’(1) if 
2. Prove that 
using the Quotient Rule.
3. Given 
find dy/dx using two different methods.
4. If f(x) and g(x) are continuous and differentiable functions with some values given by the table below, find h'(3) if 
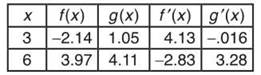
ANSWERS AND EXPLANATIONS
NOTE. Remember from the graph of ln x that ln 1 = 0.
1. The derivative of the numerator will require the use of the Product Rule, so be cautious.
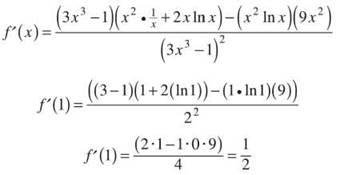
2. You can rewrite tan x as 
and use the Quotient Rule to find the derivative.
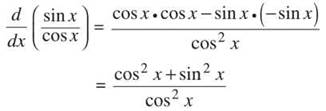
(by Mamma Theorem)
= sec2x
3. Method One: Quotient Rule
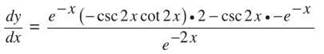
Certainly, simplification is possible, but the answer is quite messy with negative exponents.
Method Two: Product Rule
Rewrite the expression as a product, and things are much easier.
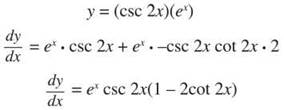
Both solutions are equivalent, although it is not obvious to the naked eye. Given a choice, Product Rule is clearly the way to go, even though the original problem was written as a quotient.
4. You may begin by factoring 1/3 out of the expression to eliminate the 3 in the denominator, but that is not required.
