Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 4. Differentiating
IMPLICIT DIFFERENTIATION
At this point in your long and prosperous calculus life, you are no longer intimidated by questions such as “Find dy/dx: y = 2sin x + 3x2.” Without a second thought (hopefully), you would answer dy/dx = 2cos x + 6x. Sometimes, however, the questions are not solved for a variable like the above problem was solved for y. In fact, some things you differentiate aren’t even functions, like the above example is a function of x. In such circumstances, you will employ implicit differentiation. In order to differentiate implicitly, you need to have a basic understanding of what it means to differentiate with respect to a variable (the previous topic in this chapter).
Steps for Success in Implicit Differentiation
ALERT! You must be at least 18 to purchase a book that discusses “explicit” differentiation.
(These steps assume that you are finding dy/dx, as it is your goal 85 percent of the time. If other variables are used, adjust accordingly.)
1. Find the derivative of the entire equation with respect to x.
2. Solve for dy/dx.
3. If a specific solution is required, substitute in the corresponding x and y values.
Example 17: Find the equation of the tangent line to the circle
x2 + y2 = 9 when x = 1
ALERT! Don’t forget to take the derivative of the constant: ![]()
Solution: In order to find the equation of a line, you need a point and a slope. It is very simple to find the point. Substitute x = 1 into the formula to find its corresponding y value. This coordinate pair (1, √8) marks the point of tangency, as shown in the figure below.
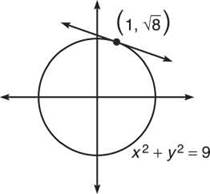
All that remains is to find the slope of the tangent line, which is given by the derivative, dy/dx. You need to find this derivative implicitly, however. To do so, first find the derivative of everything with respect to x:
![]()
To complete the problem, solve for dy/dx:
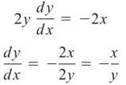
Hence, the derivative for any point (x,y) on the circle is given by the formula —x/y. Therefore, the slope of the tangent line at (1, √8) is —1/√8. Using point-slope form for a line, the equation of the tangent line is
![]()
NOTE. A normal line is perpendicular to the tangent line at the point of tangency.
Example 18: Find the equation of the normal line to sin (x) + exy = 3 when x = π.
Solution: In order to find the slope of the normal line, you need to take the opposite reciprocal of the slope of the tangent line (the derivative), since they are perpendicular. It is far from easy to solve this equation for y, so you should differentiate implicitly. Again, start by finding the point on the normal line by plugging in x = π:
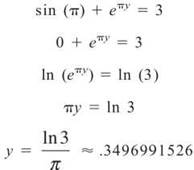
TIP. To keep resulting answers accurate, you shouldn’t round to .350 until the problem is completely over.
Thus, the tangent and normal lines both pass through (π, .3496991526).
Now, find the derivative of the equation with respect to x to get the slope of the tangent line, dy/dx:
![]()
Distribute exy and solve for dy/dx:
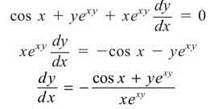
YIP. You must use the Product Rule to differentiate xy.
Plug in the coordinate (π, .3496991526) for (x,y) to get the slope of the tangent line there:

If this is the slope of the tangent line at (π, .3496991526), then the slope of the normal line is the negative reciprocal of —.0052094021, or 191.9606091 Therefore, the equation of the normal line is
y — .350 = 191.961(x - π)
(You are allowed to round at the very end of the problem on the AP test.)
EXERCISE 8
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEM 4 ONLY.
1. Find dy/dx: ![]()
2. What is the slope of the tangent line to ln (xy) + y2 = 2y at the point (e,1)?
3. Find ![]() if x2 - y2 = 16.
if x2 - y2 = 16.
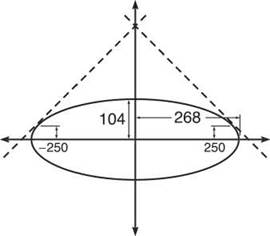
4. Dennis Franz High School (“Home of the Ferocious Prairie Dogs”) has had a top-notch track team ever since they installed their elliptical track. Its dimensions, major axis length 536 feet and minor axis length 208 feet, are close to an actual track. Below is a diagram of the Prairie Dogs’ track superimposed on a coordinate plane. If the northern boundaries of DF High are linear and tangent to the track at x = ±250 feet, find the equations of the northern property lines.
ANSWERS AND EXPLANATIONS
1. Find the derivative with respect to x.
![]()
Now, solve for dy/dx. You’ll need to factor dy/dx out of both terms on the left side of the equation.
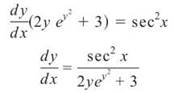
2. First, find d/dx. Remember to use the Product Rule for d/dx(xy):
![]()
Distribute 1/xy and solve for dy/dx:
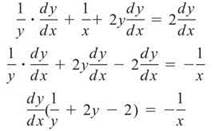
At this point, you can solve for dy/dx, but there is no real need to do so in this problem. You just want the derivative at (e, 1), so plug in those values for x and y:
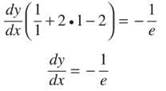
3. ![]() means the second derivative, so begin by finding dy/dx, the first derivative:
means the second derivative, so begin by finding dy/dx, the first derivative:
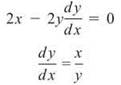
Use the Quotient Rule to find the second derivative:
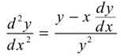
TIP. When entering fractions into the calculator, it’s a good idea to surround the numerator and denominator with parentheses.
You already know that ![]() so plug it in:
so plug it in:
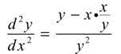
Get common denominators for y and x2/y and simplify:
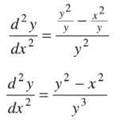
Now, the original problem states that x2 — y2 = 16, so y2 — x2 = —16. Substitute this, and you’re finished:
![]()
4. Begin by creating the equation of the ellipse. Remember, standard form of an ellipse is ![]() where a and b are half the lengths of the axes. Therefore, the track has the following equation:
where a and b are half the lengths of the axes. Therefore, the track has the following equation:
![]()
Now find the y that corresponds to both x = 250 and x = —250:
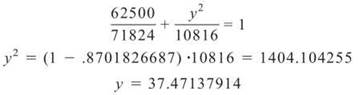
Now, you have points (±250,37.471379). Find dy/dx at these points to get the slope of the tangent lines. (Because the graph of an ellipse is y-symmetric, the slopes at x = 250 and x = —250 will be opposites.)
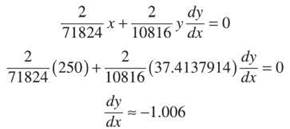
The property lines have equations y — 37.414 = —1,006(x — 250) and y — 37.414 = 1.006(x + 250).