Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 4. Differentiating
HANDS-ON ACTIVITY 4.1: APPROXIMATING DERIVATIVES
Occasionally, the AP writers can be not only tricky but maniacal as well. One such example is their new practice of asking students to find derivatives without even giving them a function.
1. A function w(t) is continuous; some of its values are listed in this table.

Draw one possible graph of w(t) for 0 ≤ t ≤ 1.
2. Although it likely won’t be exact, use a ruler to draw the tangent line to w(t) at t = .95.
3. Describe why it is impossible to find the exact value of w'(t).
____________________________________________________
____________________________________________________
4. Draw the secant line connecting t = .9 and .95. Why might this secant line be an important tool? What other secant lines could serve the same purpose?
____________________________________________________
____________________________________________________
____________________________________________________
5. Approximate w’(.95) using three different methods.
____________________________________________________
____________________________________________________
____________________________________________________
6. If a different graph, f(t), were continuous on the interval [—2,1], but you were only given the function values for t = —2, —3/2, —1, —1/2, ..., 3/2, and 2, explain how you would approximate f'(1).
____________________________________________________
____________________________________________________
____________________________________________________
SELECTED SOLUTIONS TO HANDS-ON ACTIVITY 4.1
3. In order to find the exact value of w'(t), you would need to know what rule defines w(t), not just the resulting graph.
4. The secant line has a slope that is very close to that of the tangent line. Using the very simple slope formula from algebra (∆y/∆x), you can calculate the secant slope and use it as an approximation for the derivative (tangent slope). Other secant lines that are good tangent approximators include the secant connecting (.95,3.6) to (1,3.7) and the secant line connecting (.9,3.4) to (1,3.7). All of these would be good approximations.
5. (a) Using the secant line connecting (.9,3.4) to (.95,3.6):
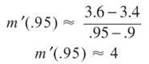
(b) Using the secant line connecting (.95,3.6) to (1,3.7):
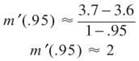
(c) Using the secant line connecting (.9,3.4) to (1,3.7):
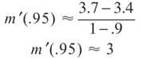
All of these are approximations, so the answers need not be the same.
6. You could find any of the following secant slopes: ![]() or
or ![]()
EXERCISE 9
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE YOUR GRAPHING CALCULATOR TO ANSWER THE FOLLOWING PROBLEMS.
Problems 1 through 4 refer to g(x) as defined by this graph:
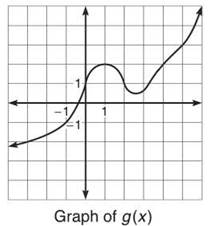
1. Give values for g(2), g(3), and g(4). Of these, which can only be an approximation?
2. Approximate h’(2).
3. Approximate the average rate of change of g(x) on the interval [—2,5].
4. Rank the following in numerical order from least to greatest: h’(—1), h'(1), h’(2).
ANSWERS AND EXPLANATIONS
1. The graph makes it pretty clear that g(2) = 1 and g(4) = 2. You’ll have to approximate g(3); according to the graph, g(3) ≈ .6.
2. The secant line connecting (1,2) and (2,1) is a good approximator; therefore, ![]()
NOTE. Problems 1 through 3 involve approximations. Your answers may not be exactly the same but may still be correct; your answer should be reasonably close.
3. The average rate of change of g(x) is given by
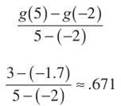
4. If you sketch tangent lines at these points, you’ll notice that the tangent line has negative slope at x = 2, zero slope at x = 1, and positive slope at x = —1. Although you do not know what the slopes actually are, you still know that negatives < 0 < positives. Therefore, h'(2) < h'(1) < h’(—1).