Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 5. Advanced Topics in Differentiation
TECHNOLOGY: FINDING POLAR AND PARAMETRIC DERIVATIVES WITH YOUR CALCULATOR (BC TOPIC ONLY)
Evaluating polar and parametric derivatives aren’t the most difficult topics you’ll encounter in AP Calculus. However, when the heat is on during the AP test and you ’re searching for that needle-in-a-haystack error you committed that is causing your answer to be mortally and inexplicably wrong, these derivatives can be pretty difficult. As you have seen in this chapter, even relatively simple polar equations can have long and yucky derivatives. There is good news—you can use your calculator to find these derivatives, and the process is very simple. To prove it to you, we’ll revisit Example 9 from earlier in the chapter, with our new calculator buddies tucked snugly in our sweaty palms.
Example 12: Find the equation of the tangent line to the parametric curve defined by x = arcsin t, y = e3t, when t = 1/√2.
Solution: Our overall approach will remain the same. We still need a point and a slope in order to construct a line. Make sure your calculator is in parametric mode ([Mode] → “Par”) and graph the equation. (You may want to adjust the graph’s [window] to see it better; I used a window of x = [-2,2] and y = [-1,15].) The point of tangency occurs (according to the problem) when t = 1/√2. To find this point in rectangular coordinates, press [2nd] → [Trace] → “value” and input t = 1/√2. The point of tangency is (.707,8.342), just as we got previously.
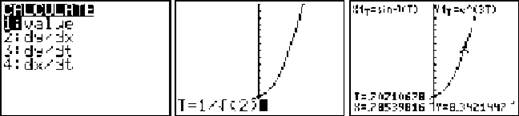
In order to find the derivative when t = 1/√2 go back to the [Calc] menu and this time select dy/dx. Enter 1/√2 for t as you did last time, and dy/dx = 17.696.
NOTE. Your calculator can find points of tangency for polar graphs, too. This (like everything else) is also found in the [Calc] menu.
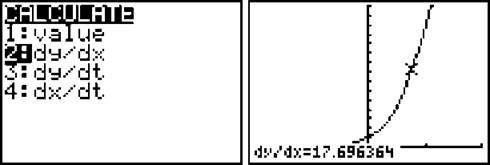
The equation of the tangent line, then, is
y - 8.342 = 17.696(x - .707)
Polar derivatives are just as easy with the calculator. Who’s up for reruns? Let’s enjoy Example 10 a second time, this time with our lil’ computing buddy by our side.
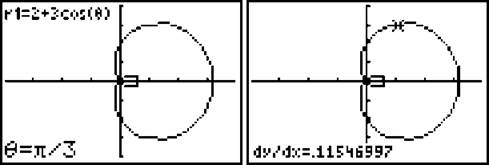
Example 13: Find the slope of the tangent line to r = 2 + 3cos θ if θ = π/3.
Solution: Make sure to set the calculator to Polar mode ([Mode] → “pol”) and graph the equation. Because this graph has trigonometric equations, it’s a good idea to choose [Zoom] → “Ztrig” (window settings that are friendly to trigonometric graphs). Much like Example 11, you proceed to the [Calc] menu ([2nd] → [Trace]) and select dy/dx, the derivative. The calculator then prompts you to input θ; type in π/3 (as shown below), and the derivative appears as if by magic: dy/dx = .115.
It’s worth repeating that you must know how to calculate points of tangency and derivatives without a calculator, although no one would argue that the calculator doesn’t make it significantly easier.
EXERCISE 6
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 4 THROUGH 8 ONLY.
1. Use a linear approximation at x = 1/2 to estimate m(.502) if 
--------------------------------------------------------
2. Evaluate 
*3. Find dy/dx at θ = 7π/6 for the polar equation r = sin θ cos θ.
*4. At what values of t does 
for the parametric function defined by x = 2 + t2, y = 3 - t?
*5. If f(x) = 2tan x + x3 and g(x) is a continuous, origin-symmetric function that contains the following values:
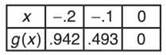
Estimate 
*6. Find the equation of the vertical tangent line (in rectangular form) to the curve defined by the parametric equations x = e t sin t, y = 2t + 1, 0 ≤ t < 2π.
7. If k(x) = 2x3 + x + 2, what is the equation of the tangent line to k-1(x) when x = 4.3?
*8. At what rectangular coordinates do the tangent lines to r = sin2θ at θ = π/6 and θ = 2π/5 intersect? (Note: Answer this as you would a free response question. Show all work, and make sure to include the setup for any answers you give based on calculator work.)
9. James’Diabolical Challenge: Let 
(a) Evaluate f-1(0).
(b) Find (f-1)' (0).
*(c) What is 
?
*a BC-only question.
ANSWERS AND EXPLANATIONS
1. We have to begin by finding the equation of the tangent line to m at x = 1/2. We determine the point of tangency by calculating m(1/2).
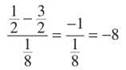
The point of tangency, therefore, is (1/2,-8). The slope of the tangent line will, as always, be given by the derivative, so use the Quotient Rule to find it:
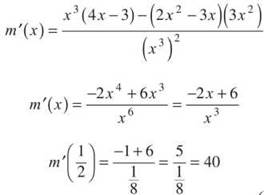
Therefore, the equation of the tangent line is y + 8 = 40 (x – 1/2).
Last step: Substitute x = .502 into the tangent line to get the linear approximation:
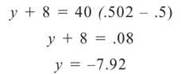
(If you plug the answer into the original equation, m(1/2) = -8, so this approximation is relatively close.)
2. L’HopitaTs Rule is too cumbersome for this problem. Notice that you have a rational function with the same degree (√x = x) in the numerator and denominator. Thus, the limit at infinity will be the ratio of the numerator’s and denominator’s leading coefficients: √3/5.
3. In order to find dy/dx you first must express the equation parametrically: x = sinθ cos2θ, y = sin2θ cosθ. Remember that dy/dx is basically y’/x’. You’ll need to use the Product Rule to get x’ and y’:
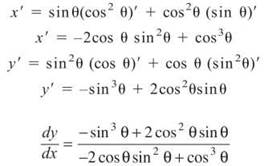
Now, evaluate dy/dx for θ = 7π/6:
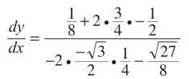
Of course, there is no need to simplify this answer, and doing so drastically increases your chances of making a mistake. If you simplifed further and want to know if you got it right, use a calculator to evaluate your expression; it should equal 2.887.
4. First, find dy/dx:
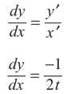
Clearly, the derivative will equal 1/2 whenever t = -1.
5. If you try to evaluate the limit via substitution, you will get indeterminate form 0/0, so you should default to L’Hopital’s Rule and find 
Simple differentiation yields f’(x) = 2sec2x + 3x2, so f'(0) = 2 ∙ 1 + 0 = 2. To complete the problem, however, you’ll also need g'(0), and that will require some estimation. Because g is origin symmetric, you automatically know that g(.1) = -.492 and g(.2) = -.942. You should use one of the following secant lines to estimate the derivative: from x = -.1 to .1, from x = -.1 to 0, or from 0 to .1. If you choose the secant line from -.1 to 0, the secant slope is 
Therefore, 
6. The slopes of all tangent lines, vertical or not, are furnished by dy/dx, so begin by finding it:
A vertical asymptote will occur when the denominator is 0 but the numerator is not. This numerator is always 2, so you need only determine where the denominator is 0. You can use your calculator to solve this, but the problem is pretty easy without the calculator:
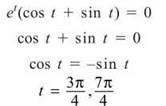
NOTE. You need only worry about (cost + sin t) being equal to 0 in problem 6 because et never equals 0 (the range of ex is y > 0).
However, this is not the answer to the question. Instead, you need to give the rectangular equations of the vertical tangent lines that occur at these values of t. To do so, use the [2nd] → [Tr ace] →“value” function of your calculator. When t = 3π/4, the corresponding rectangular coordinate is (7.460,5.712); when t = 7π/4, the corresponding coordinate is (—172.641,11.996). Therefore, the equations of the vertical tangent lines are x = 7.460 and x = -172.641.
7. You’ll need, as always, a point and a slope to form a line. You cannot find k-1(x) algebraically, so you ’ll need to use the Magnum P.I. formula to find the derivative of the inverse function and, hence, the slope of the tangent line:
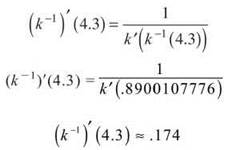
Now that you have the point and the slope, it is a trivial pursuit to write the equation of the line (although I always have trouble with those entertainment questions):
y - .890 = .174(x - 4.3)
CAUTION. You cannot use the [2nd]->[Trace]-> “intersection” feature of your calculator on the free-response portion of the test, so use the equation solving feature of the calculator instead.
8. Use the calculator’s [2nd] → [Trace] → “value” and [2nd] → [Trace]“dy/dx” functions to calculate the points of tangency and derivatives for each line. The tangent lines should be
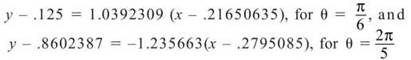
To find the intersection of these lines, solve both for y and set them equal to each other:
You can now solve the equation on your calculator by setting the above equation equal to 0 and finding the root:
Substitute this value into either line’s equation to get the corresponding y-value, and the resulting coordinate is (.574, .496).
9. (a) To find f-1 at a specific x, set f equal to x and solve:
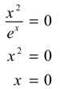
Therefore, f-1(0) = 0.
(b) This requires the inverse function derivative formula. Apply the information from 9(a), and the formula becomes
If you find f'(x) with the Quotient Rule, you get
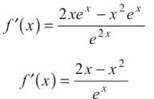
Therefore, f'(0) = 0; substitute this into the inverse function derivative formula:
(f-1)'(0) is undefined; the inverse function is not differentiable there due to a vertical tangent line.
(c) To find this limit, you must apply L’Hopital’s Rule twice (due to the presence of indeterminate form ∞/∞):
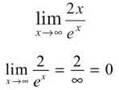
SUMMING IT UP
• The Power, Product, Quotient, and Chain Rules allow you to find the derivative in almost any expression or equation you will encounter.
• Inverse functions are helpful in their power to cause other functions to disappear.
• Linear approximations are the first step in a more complicated process known as Euler’s Method. Whereas approximations are on both the AB and BC tests, Euler’s Method appears only on the BC test.
• When applying L’Hopital’s Rule, find the derivatives of the numerator and denominator separately. Do not use the Quotient Rule to find the derivative of the entire fraction.
• L’Hopital’s Rule is for use only with indeterminate limits.
• Even though your graphs are done in polar mode, all equation-solving with the calculator (using v-intercepts) requires that you switch back to rectangular mode first.