Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 6. Applications of the Derivative
HANDS-ON ACTIVITY 6.1: ROLLE’S AND MEAN VALUE THEOREMS
The following activity will help you uncover two of the most foundational theorems of differential calculus. Rolle’s Theorem is one of those rare calculus theorems that makes a lot of sense right away. The Mean Value Theorem is not very difficult either, and it usually appears on the AP test pretty frequently. With your deep conceptual understanding of derivatives, you should have no problem at all understanding.
ALERT! Same students confuse the Mean Value Theorem with the Intermediate Value Theorem. They are similar only in that they are both existence theorems, in that they guarantee the existence of something.
1. Let’s say that you have the continuous and differentiable function f(x) = x3 — 6x2 + 12x — 5. Draw the portion of the graph indicated by the axes below (x = [0,4]).
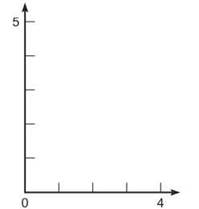
2. Draw the secant line that connects x = 1 to x = 3 on the graph off and calculate the slope of the secant line.
________________________________________________________
________________________________________________________
3. Are there any places on the graph of f where the tangent line to the graph appears to be parallel to the secant line you’ve drawn? How many times does this happen on [0,3]? Draw these tangent lines that appear to be parallel to the secant line.
________________________________________________________
________________________________________________________
4. What does it mean geometrically if those tangent lines are parallel to the secant line?
________________________________________________________
________________________________________________________
5. Write your conclusion to problem 4 as a mathematical formula. If you solve this for x (you’ll have to use your calculator), you will find the x values for the tangent lines. What are they?
________________________________________________________
________________________________________________________
________________________________________________________
TIP. The Mean Value Theorem is so named because of the large role the average, or mean, rate of change plays in the theorem.
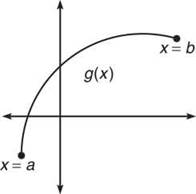
6. Time to be generic. Given a continuous, differentiable function g(x) on the interval [a,b], complete the following:
• Give the slope of the secant line from x = a to x = b.
________________________________________________________
• Give the slope of the tangent line to g(x) at any point on its domain.
________________________________________________________
Use your answers above to fill in the blanks and complete the Mean Value Theorem:
Mean Value Theorem: Given a function g(x) that is continuous and differentiable on a closed interval [a,b], there exists at least one x on [a,b] for which _______, the slope of the secant line, equals _______, the slope of the tangent line.
7. Illustrate the Mean Value Theorem graphically using the graph below of g on [a,b].
8. Translate the Mean Value Theorem into a statement about rates of change.
________________________________________________________
________________________________________________________
9. Rolle’s Theorem is a specific case of the Mean Value Theorem, which applies whenever g(a) = g(b). What is the slope of the secant line for such a function? What is guaranteed by the Mean Value Theorem as a result, and what does that mean geometrically?
10. Fill in the blanks to complete the theorem:
Rolle’s Theorem: Given a function f(x) that is continuous and differentiable on the closed interval [a,b] and ___ = ___, then there exists at least one x on [a,b] such that _______.
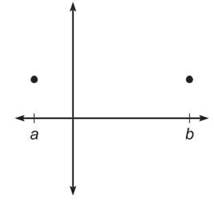
11. Draw a function g(x) on the axes below that satisfies Rolle’s Theorem on [a,b] but satisfies it more than one time.
SELECTED SOLUTIONS TO HANDS-ON ACTIVITY 6.1
2. The slope of the secant line is 
3. There are two places on [0,3] where the tangent lines appear to be parallel—one falls nearly midway between x = 1 and 2 and another between x = 2 and 3.
4. It means that they share the same slope.
5. The formula should state that the secant and tangent slopes are the same:
The left-hand formula is the secant slope, and the derivative on the right represents the tangent slope. You already know the secant slope, so f’(x) = 1. Find f'(x) and solve using your calculator; you should get x ≈ 1.423 and x ≈ 2.577.
6. The secant slope is 
and tangent slope is g'(x).
Mean Value Theorem: ...there exists at least one x on [a,b] for which 
equals g'(x).
7. Estimate on the graph where the secant and tangent lines appear to be parallel.
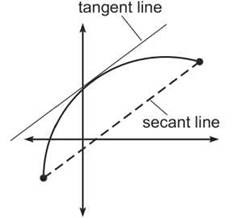
8. At least once on the interval [a,b], the instantaneous rate of change equals the average rate of change for that interval.
NOTE. The fact that a derivative of 0 indicates a possible maximum or minimum on the graph is an incredibly important fact as this chapter progresses.
9. The slope of the secant line is 0, so the Mean Value Theorem guarantees that somewhere on [a,b], there will be a horizontal tangent line. Geometrically, this means that the graph reaches a maximum or a minimum somewhere between a and b, assuming, of course, that the function is not merely a horizontal line connecting (a,f(a)) to (b,f(b)).
10. Rolle’s Theorem: ...[a,b] and f(a) = f(b), then there exists at least one x on [a,b] such that f’(x) = 0.
11.
EXERCISE 2
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEM 5 ONLY.
1. Determine if each of the following statements is true or false. If true, justify your answer. If false, provide a counter example.
If f(x) is a continuous function on [a,b], and f(a) = f(b), then ...
(a) f has an absolute maximim and an absolute minimum.
(b) There exists a c, a ≥ c ≥ b, such that f’(c) = 0.
2. During vacation, Jennifer is en route to her brother’s house. Unbeknownst to her, two policemen are stationed two miles apart along the road, which has a posted speed limit of 55 mph. The first clocks her at 50 mph as she passes, and the second measures her speed at 55 mph but pulls her over anyway. When she asks why she got pulled over, he responds, “It took you 90 seconds to travel 2 miles.” Why is she guilty of speeding according to the Mean Value Theorem?
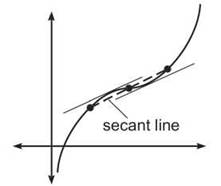
3. Given g(x) as defined by the graph below, and g(b) = g(c).
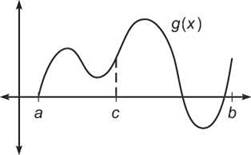
(a) How many times does g(x) satisfy the Mean Value Theorem on [a,b]?
(b) What conclusions, if any, can be drawn about g(x) using Rolle’s Theorem?
4. At what value(s) of x is the Mean Value Theorem satisfied for m(x) = x3 – 5/2x2 – 2x + 1 on [-2,4]?
5. If h’(0) satisfies the Mean Value Theorem for h(x) = ln (sin x +1) on [—π/4,b], find the smallest possible value of b.
ANSWERS AND EXPLANATIONS
1. (a) True: This value is guaranteed by the Extreme Value Theorem; the function need only be continuous on a closed interval.
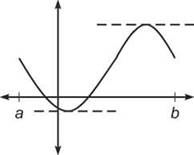
(b) False: It may sound like Rolle’s Theorem, but Rolle’s Theorem includes the guarantee that the function is differentiable on [a,b]; the diagram below shows one possible graph off for which there is no horizontal tangent line on the interval.
NOTE. In fact, Jennifer probably went a whole lot faster than 80 mph when she thought no one was looking, but the Mean Value Theorem can only do so much.
2. You can figure out Jennifer’s average speed for the two miles between the police; think back to the old, familiar formula d = rt (distance = rate ∙ time). Her rate will be given by r = d/t. Your units are hours, so 90 seconds has to be rewritten in terms of hours. Because there are 3,600 seconds in an hour, 90 seconds represents 90/3,600 of an hour, or 1/40. Clearly, d = 2 from the information given. Therefore, you can find the average rate of speed:
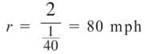
The Mean Value Theorem says that on a closed interval, your instantaneous rate of change (in this case, velocity) must equal the average rate of change (average speed) at least once. Therefore, ol’ leadfoot Jenny had to have traveled 80 mph at least once, and the policeman can ticket her.
3. (a) The tangent line must be parallel to the secant line (shown dotted in the diagram below) four times in that interval at approximately the places marked below.
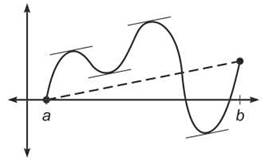
(b) Rolle’s Theorem ensures that g'(x) = 0 at least once between x = c and x = b. In fact, g'(x) = 0 twice on the interval, although you may not be able to justify that visually until later in this chapter.
4. The Mean Value Theorem states that at some point c between —2 and 4,
Once you find m'(c) and evaluate the fraction, you can solve for c:
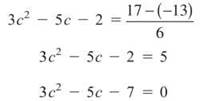
This doesn’t factor, so you need to resort to the quadratic formula. The solutions are 
However, only the solutions on the interval [—2,4] count. Without a calculator, how can you tell if either of these fall in the interval? Well, √109 is between √100 (10) and √121 (11). If you evaluate the solutions with these estimations in place, both answers fall within the interval, so both values of c are correct.
5. If the Mean Value Theorem is satisfied at h'(0), then the average rate of change on the interval must be equal to that value; that value is
Therefore, all you need to do is to find the average value and set it equal to 1 in order to find b:
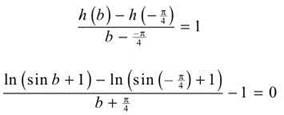
Once you set this gigantic equation equal to zero, you can use your calculator to solve, and b ≈ 1.07313.