Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 6. Applications of the Derivative
CONCAVITY
Two of the major characteristics used to describe graphs are direction and concavity. You have already used the sign of the first derivative to determine the direction of a function, and in this section, you will use the sign of the second derivative to determine the concavity of the original function. In 1955, prison wardens all over the world introduced fluoride into the drinking water of their prisons in a coordinated effort to reduce “con” cavities, but their efforts proved to be in vain. Thus, concavity still pervades functions worldwide.
Concavity describes the curviness of a curve. Consider the mouths on the faces drawn below:
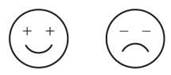
The smile on a happy face is described as concave up, whereas the frown is concave down. Notice that frown and down rhyme. It is also said that milk poured into a concave up curve stays there, whereas milk poured on a concave down curve will splatter on your mom’s clean floor and make her angry. In this mnemonic device, a cup should be concave up.
Notice the signs that constitute the eyes of the faces; these signs remind us of the most important fact concerning concavity: If a function, fix), is concave down on an interval, then the second derivative, f"(x), will be negative there. Similarly, if a function is concave up, its second derivative will be positive.
This is hauntingly similar to our work with direction and the first derivative. In that case, the sign of the first derivative indicated direction. Concavity, on the other hand, is dictated by the sign of the second derivative. This relationship is explored by the diagram below:
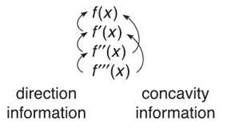
The sign of a function describes the direction of the function one step “above” it, and that same sign describes the concavity of the function two steps “above.”
Example 4: On what intervals is the graph of the function g(x) = x3 — 2x2 — 4x + 2 concave down?
Solution: The concavity of a function is based on the sign of its second derivative, so you need to begin by finding g"(x):
g'(x) — 3x2 — 4x — 4
g"(x) = 6x — 4
Here, you need to find critical numbers again, just as you did when you found direction. This time, the critical numbers occur when the second derivative is either zero or undefined. The only critical number is x = 2/3. Use this to create a second derivative wiggle graph, and make sure to label it g". Choose test numbers from both of the intervals and make sure to plug them into the second derivative, as it is the sign of the second derivative that provides the information you are seeking. The wiggle graph looks like the following when you are finished:
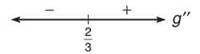
The graph of g(x) is concave down on (—∞,2/3).
In the preceding example, the graph changed from concave down to concave up at the point (2/3, —34/27). The change of concavity makes this a point of inflection, much as a change of direction caused points to become extrema points.
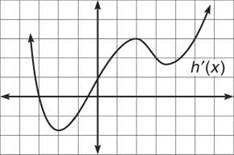
Example 5: Given the graph below of h'(x), the derivative of h(x), describe the concavity of h(x).
TIP. Just as you used the wiggle graph to describe direction and direction changes, you’ll use a second derivative wiggle graph to describe concavity and concavity changes.
Solution: Not only does the h"(x) describe the concavity of h(x), but it also describes the direction of the h’(x). (Since h'(x) is one step “above” h"(x).) From the graph, you can tell that h'(x) is increasing on (—2,2) ∪ (3.5,∞) and decreasing on (—∞,—2) ∪ (2,3.5). Therefore, h"(x) will be negative on (—∞,—2) ∪ (2,3.5) and positive on (—2,2) ∪ (3.5,∞), as indicated on the concavity wiggle graph below:
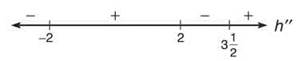
TIP. Do you see why it’s so important to label your wiggle graph? Without the h" label in Example 5, it wouldn’t be immediately obvious which derivative we were referencing.
Without having seen a graph of h(x), we can draw from the concavity wiggle graph that h is concave up on (—2,2) ∪ (3.5,∞) and concave down on (—∞,—2) ∪ (2,3.5).
EXERCISE 4
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 3 AND 4.
1. Describe the concavity of the generic linear function y = ax + b, and interpret your answer.
2. On what intervals is the function ![]() concave up on the interval [0,2π]?
concave up on the interval [0,2π]?
3. Given the differentiable graph of f"(x) below, answer the following questions:
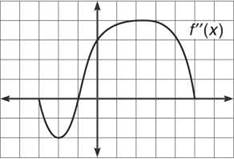
(a) Describe the concavity of f(x).
(b) At what x-values will f'(x) have its absolute maximum and absolute minimum values?
(c) Will f"'(0) be positive or negative? What about f(4)(0)?
(d) On what intervals will f'(x) be concave down?
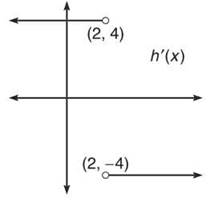
4. Given the below graph of h'(x), describe the concavity of h(x), given h(x) is continuous.
ANSWERS AND EXPLANATIONS
1. The concavity of a function is described by its second derivative, so find that first:
y' = a
y" = 0
It is difficult to interpret a value of zero in the second derivative. In this case, it is because a line by itself does not have any concavity. However, a second derivative of 0 does not always mean that no concavity exists (see problem 4).
2. It’s necessary, again, to find the second derivative. Instead of using the Quotient Rule, use a double angle formula to simplify the fraction first:
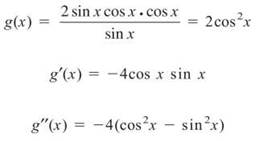
Set the second derivative equal to 0, and solve to get critical numbers of π/4, 3π/4, 5π/4 and 7π/4. Use these and test points from each interval to construct the following wiggle graph for concavity:
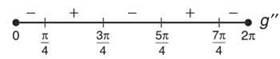
Therefore, g(x) will be concave up on the intervals (π/4, 3π/4) and (5π/4, 7π/4).
3. (a) f"(x) is negative on (-3,-1), so f(x) will be concave down there. However, f(x) will be concave up on (-1,5), since f"(x) is positive on that interval.
(b) Because f"(x) is negative on (-3,-1), you know that f'(x) is decreasing on that interval. However, f’(x) will be increasing on the interval (-1,5) by the same reasoning. Notice that the graph changes from decreasing to increasing at x = -1, so a relative minimum will occur there. That relative minimum will also be the absolute minimum of the graph, because the graph only increases once you pass that point. Because the graph increases for the remainder of its domain, the absolute maximum of the graph will occur at x = 5, which is the last defined point on the graph.
(c) The third derivative off describes the direction of the second derivative of f. You are given the graph of the second derivative, and at x = 0, f"(x) is increasing, so f'"(0) will be positive. On the other hand, f(4)(x) describes the concavity of f"(x), and the graph of f"(x) is concave down at x = 0. Therefore, f(4)(0) will be negative.
(d) The signs of f"'(x) will describe the concavity of f'(x). How do you determine the signs for f"'(x)? Remember that it describes the direction of f"(x). Because f"(x) decreases on (-3,-2) ∪ (2,5) and increases on (-2,2), you can construct the following wiggle graph of f'"(x):
![]()
Therefore, f'(x) will be concave down on (—∞,—2) ∪ (2,∞).
TIP. A relative extrema point is the highest or lowest value in a small interval of the graph. An absolute extrema point is the highest or lowest point on the entire domain of the graph. Absolute extrema can occur at relative extrema or end points, if the function has them.
NOTE. A position equation describesan object’s motion by giving its position at any time.
4. This requires some thinking. The graph tells you that h(x) is some function whose derivative is consistently 4 until x = 2, and then the derivative suddenly changes to —4. What kind of a function has a constant derivative? A linear function. For example, if y = 4x + 3, then y' = 4. Flowever, what sort of linear function suddenly changes derivative? Consider the absolute value graph pictured below:
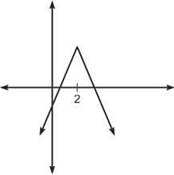
The slope of the curve is 4 until x = 2, at which point the slope turns into its opposite, —4. The graph of h(x) is concave down on its entire interval.