Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 7. Integration
THE TRAPEZOIDAL RULE
Sure, Riemann sums give some approximation of the area under a curve, but they sure as heck don’t give a terrific approximation. In fact, they’re as clumsy as your cousin Irene that time she fell down the stairs at your parents’ barbeque. There are other, more accurate, methods and this section focuses on one of them. (The other major method, Simpson’s rule, is no longer on the AP test. D’oh! It used intervals with little parabolas on the end to approximate area.)
Consider the following graph and the method of upper sums used to approximate the area it bounds.
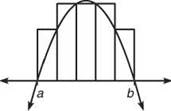
There’s no avoiding it or ignoring it any longer: Those rectangles just contain way too much extra space. Enter (to thunderous applause) the Trapezoidal Rule. Instead of little rectangles, we will use little trapezoids to approximate the area.
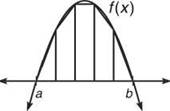
A Cunning Trapezoidal Rule Problem
These trapezoids are formed by marking the function values at both endpoints of an interval and connecting the two dots. See how all that extra area disappears in just one application, returning the original showroom shine to the car’s finish? You also may have noticed that the two “trapezoids” at the edges are really triangles. That’s okay. Believe it or not, a triangle is just a special kind of trapezoid (a trapezoid with one base that has length 0). These aren’t the pretty trapezoids you’re used to seeing, but remember, a trapezoid is a quadrilateral with exactly one pair of parallel sides, and the vertical sides of these trapezoids are their bases.
According to geometry (and the voices echoing in my head), the area of a trapezoid is
where h is the height of the trapezoid and b1 and b2 are the lengths of its parallel sides, or bases.
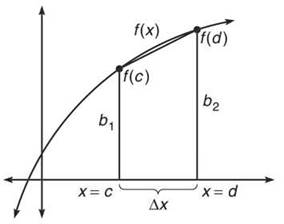
The bases in the above trapezoid have length f(c) and f(d), and the height, h (the distance between the bases), is d — c, or ∆x.
Let’s return to the diagram above, entitled, “A Cunning Trapezoidal Rule Problem,” and determine the area according to the Trapezoidal Rule. In that problem, we know there are 5 trapezoids, but let’s pretend we don’t and say that there are n trapezoids. This way, we can develop the Trapezoidal Rule from scratch.
The area of the first trapezoid (conveniently labeled trapezoid 1) will be 
To find the height, remember the formula from the section on Riemann sums:
therefore,
The area of the second trapezoid is 
(The h will have the same value, since our intervals will always be of equal measure.) So far, the area is
Let’s skip ahead to the sum of all the trapezoids.
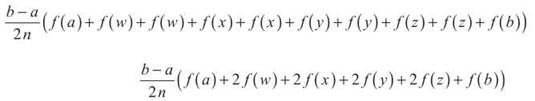
This, in essence, is the Trapezoidal Rule, but let’s define it carefully:
The Trapezoidal Rule: If f is a continuous function on [a,b] divided into n equal intervals of width 
as pictured in the diagram below, then the area between the curve and the x-axis is approximately
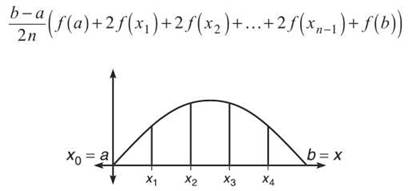
Translation: In order to approximate the area beneath the curve f(x), find the width of one interval 
and divide it by 2. Then multiply by the sum of all the function values doubled, but don’t double f(a) or f(b), the beginning and ending function values.
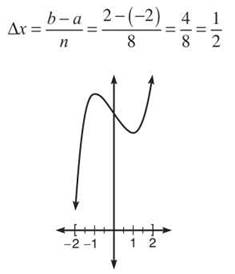
Example 4: Use the Trapezoidal Rule to approximate the area beneath the curve f(x) = x3 — 2x + 5 on [—2,2] using n = 8 subintervals.
ALERT! Even though the Trapezoidal Rule contains 
the width of the trapezoids is still 
Know when to use each expression.
Solution: If 8 subintervals are used, then the width of each will be
You can then apply the Trapezoidal Rule, using the x values 
and 2:
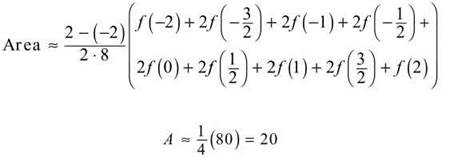
In fact, this is the exact area beneath the curve, although you don’t know how to verify this yet—that’s in the next section.
EXERCISE 3
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEM 3 ONLY.
1. The Trapezoidal Rule can give the exact area beneath what types of functions?
2. Use the Trapezoidal Rule to approximate the area beneath the curve h(x) = x2 + 1 on the interval [0,4] using
(a) 2 subintervals
(b) 4 subintervals
(c) 3 subintervals
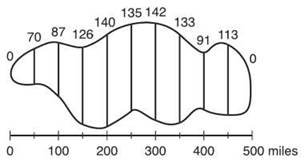
3. (Based on the Stephen King book The Girl who Loved Tom Gordon) Nine-year-old Trisha McFarland is hopelessly lost in the woods, and the efforts of those looking for her have turned up nothing. The graph below shows the woods in which she is lost and measurements of the width of the woods (in miles) at regular intervals.
(a) Use the Trapezoidal Rule to approximate the area of the woods.
(b) Assuming that one person can search 15 mi2 in one day, how many people will it take to scour the entire woods in a single day?
ANSWERS AND EXPLANATIONS
1. The Trapezoidal Rule gives the exact area beneath linear functions, since the tops of the trapezoids used to make the approximations are linear.
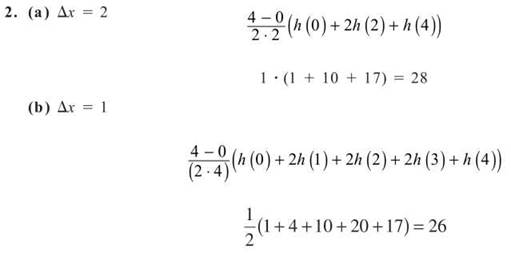
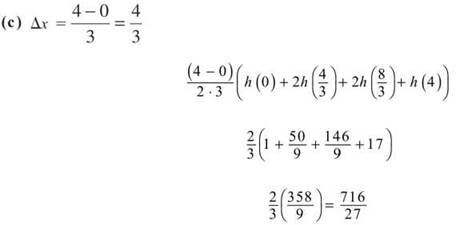
By the way, 716/27 is approximately 26.519.
TIP. The number of terms you add in the Trapezoidal Rule is always one more than the n you are using.
3. It might confuse you that the woods wiggle around as they do. If it helps, you can smoosh the woods against the x-axis to look something like this:
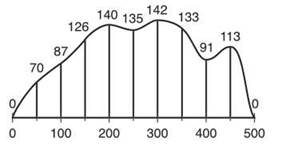
Either way, it is clear that f(100) = 87, f(350) = 133, and so on. The Trapezoidal Rule is actually quite easy to apply; you don’t even have to plug into a function to get its values, as you did in number 2. The graph clearly is defined on the interval [0,500], and there are 10 subintervals, each with a length 50 miles.
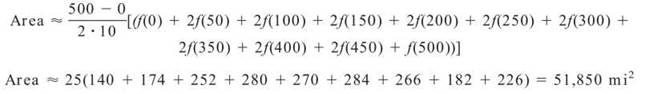
(b) Even though 15mi2 is a generous estimate of how much area one person can search, it would take
at least 3,457 people to conduct the search simultaneously.