Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 2. Calculus Prerequisites
FUNCTION PROPERTIES
Once a relation is classified as a function, the fun is only just beginning. Functions exhibiting other specific properties allow us to deepen our ever-widening puddle of understanding. For example, some functions can be classified as even. An even function is so mathematically robust that a negative input does not affect the function at all. Consider the function f(x) = x2 — 3, and compare f(4) to f(—4). Upon substituting, it is clear that f(4) = f(—4) = 13. Opposite elements of the domain result in the same output. Thus, f(x) exhibits the property that allows us to classify it as even. Mathematically, we write: If f(—x) = f(x), then f(x) is even, which means that evaluating the function at a negative input, —x, results in the original function, f(x).
Example 6: Prove that m(x) = 5x4 — 2x2 + 7 is even, whereas b(x) = x2 + 8x is not even.
Solution: In order to test m, you substitute —x into the function to get m(—x) = 5(—x)4 — 2(—x)2 + 7 = 5x4 — 2x2 + 7 = m(x).
Because m(—x) = m(x), the function is even. Similarly, test b:
b(—x) = (—x)2 + 8(—x) = x2 — 8x ≠ b(x)
Thus, b is not even.
Be careful! It is just plain wrong to assume that because b is not even, it must be an odd function. Though that assumption is true with integers, it is not true with functions. In fact, for a function to be odd, it must satisfy a completely different property: If g(—x) = —g(x), then g(x) is said to be odd. Whereas the terms in an even function stay exactly the same for an input of —x, each of the terms of an odd function will become its opposite.
Example 7: Show that the function d(x) = x5 — 3x is odd.
Solution: Notice that d(—x) = (—x)5 — 3(—x) = — x5 + 3x = —d(x). Therefore, d is odd. All of the terms must change sign (as they did in this problem) in order for the function to be odd.
ALERT! If a function does not fulfill the requirements to be even or odd, the function is classified as “neither even nor odd.”
Another important property of a function is the symmetry, if any, that is evident in its graph. A graph is called symmetric if it is exactly the same (or mirrored) on both sides of some arbitrary line or point. For example, the graph of y = x2/3, below, is described as y-symmetric because the graph is identical on either side of the y-axis. All y-symmetric graphs have this defining property: if a point (x,y) lies on the graph, so must the point (—x,y).
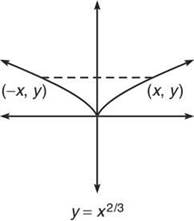
Notice that the sign of the input to the function does not matter—both r and —x result in the same y. Does that sound familiar? It should! That’s the definition of an even function. Therefore, all even functions are y-symmetric and vice versa.
The other type of symmetry that is very common to calculus is origin-symmetry. If a graph (or function) is origin-symmetric, then all points (x,v) on the graph must have a corresponding (—x,—y), as displayed in the graph below, the graph of y = x3 — x.
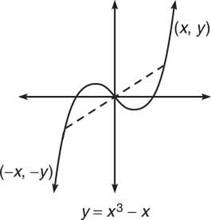
Using the same reasoning as above, all odd functions are origin-symmetric.
TIP. It is easy to remember that origin-symmetric functions are odd—they both start with the letter “o.”
Example 8: Determine what symmetry, if any, is evident in the function h: {(3,5),(4,-1),(0,0),(-3,-5),(-4,1)}.
Solution: The function h is origin-symmetric, since every (x,y) is paired with a corresponding (—x,—y).
EXERCISE 2
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 7 THROUGH 9.
In problems 1 through 6, determine if the given function is even, odd, or neither.
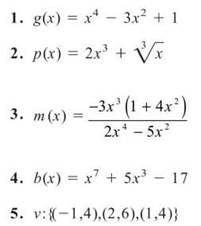
6.
7. The equation x = y2 has an x-symmetric graph. In x-symmetric graphs, if the point (x,y) is contained, then so is (x,—y). Why aren’t x-symmetric functions used as often as y- and origin-symmetric functions in calculus?
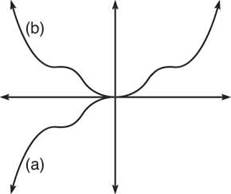
8. Complete the below graph of f if...
(a) f is odd
(b) f is even
9. If j(x) and k(x) are odd functions and 
what kind of symmetry characterizes h?
ANSWERS AND EXPLANATIONS
1. g is even: g(—x) = (—x)4 — 3(—x)2 + 1 = x4 — 3x2 + 1 = g(x).
2. p is odd: 
Remember that 
3. m is odd. No signs will change in m(—x), except —3x3 will become 3x3. Thus, the entire fraction (all one term) changes from negative to positive, and m(—x) = —m(x).
4. b is neither even nor odd: b(—x) = (—x)7 + 5(—x)3 — 17 = — x7 — 5x3 — 17 ≠ b(x). Because the —17 does not change signs like all the other terms, b is not odd; b is clearly not even, either.
5. v is neither even nor odd. You might think the function is even since the pair of points (— 1,4) and (1,4) are present. However, (—2,6) would also have to be present to make the function even.
6. r is neither even nor odd since there is no y- or origin-symmetry.
7. The vast majority of x-symmetric graphs are not functions, as they fail the vertical line test. Note that the single input x results in two outputs, y and —y, which is forbidden in the happy land of functions.
8.
9. To test h(x), you proceed as usual: 
Since j and k are odd, you know that 
Therefore, h is even, as the negative signs will cancel out, making h(x) y-symmetric by definition.