Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 7. Integration
TECHNOLOGY: EVALUATING DEFINITE INTEGRALS WITH YOUR GRAPHING CALCULATOR
The final of the four calculator skills (also known as the four skills of the apocalypse by those lacking technological know-how) you are required to know for the AP test is how to calculate a definite integral. As was the case with derivatives, the TI-83 cannot find symbolic integrals. In other words, it does not know that ![]() However, it can find a darn good approximation for the area beneath a curve. Always remember and never forget that you’ll have to be able to solve definite integrals without your graphing calculator, so don’t come to rely so much on the tool that you forget the Fundamental Theorem in all its glory.
However, it can find a darn good approximation for the area beneath a curve. Always remember and never forget that you’ll have to be able to solve definite integrals without your graphing calculator, so don’t come to rely so much on the tool that you forget the Fundamental Theorem in all its glory.
Example 17: Evaluate ![]()
Solution: This was problem 1(a) from the Fundamental Theorem problem set; although it wasn’t very hard, there are lots of places to make a mistake. To use your calculator, press [Math], [9], or just press [Math] and arrow down to the 9th option, “fnInt.”The correct syntax for evaluating definite integrals on the TI-83 is
fnlnt(integral,x,lower lim it,upper limit)
Type this into your calculator,
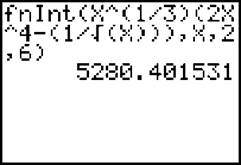
and you get 5,280.402. Are you convinced that this is the same thing as the answer we got back in the pre-calculator day?
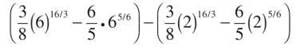
To make sure they are the same (if you feel the need, are masochistic, or are, by nature, dubious of others), you can type the above “number” into your calculator, and see what happens.
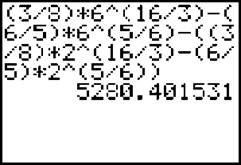
Oh, ye of little faith—they’re the same.
EXERCISE 9
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 11 THROUGH 13 ONLY.
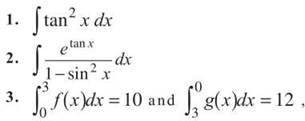 evaluate the following:
evaluate the following:
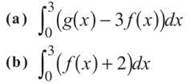
4. Evaluate 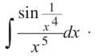
5. What is the average value of the function ![]()
6. Set up, but do not evaluate, ![]()
7. If ![]()
8. What expression has an integral of 31n |m(3x)| + C , if m is a function of x?
9. ![]()
10. The following graph, r(t), represents the rate of sales of the Furby toy (in hundreds of thousands of toys per month) from January 1998 to June 1999.
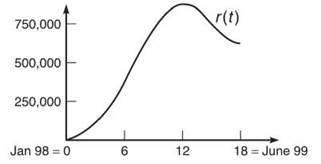
(a) Write a definite integral that represents total sales from February 1998 to March 1999.
(b) Write, but do not evaluate, an expression that represents the average rate of sales over the entire period of time.
(c) Where will the graph of total sales be concave up?
11. If ![]() (a and b are real numbers), find a in terms of b.
(a and b are real numbers), find a in terms of b.
12. If it takes NASCAR driver Dale J arrett 1 minute to complete a lap around a track and his speed is measured every 10 seconds (in mph) as indicated below, answer the following.
|
time |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
speed(mph) |
0 |
98 |
117 |
225 |
233 |
228 |
241 |
(a) According to midpoint sums and n = 3 rectangles, approximately how long is one lap on the track?
(b) What estimation of Dale’s distance traveled is given by the Trapezoidal Rule with n = 6 trapezoids?
(c) Using your results from part (b), approximate Dale’s average speed.
13. James’ Diabolical Challenge: Aparticle’s velocity over time (in inches/sec) as it moves along the x-axis is governed by the function v(t) = 3t2 — 10t + 15.
(a) If the particle’s position at t = 1 second is 8 inches, find the exact position equation of the particle, s(t).
(b) What is the distance traveled by the particle from t = 0 sec to t = 5 sec?
(c) At what time(s) from t = 0 sec to t = 5 sec is the particle traveling its average velocity?
ANSWERS AND EXPLANATIONS
1. If you use the Pappa Theorem to rewrite tan2 x as sec2 x — 1, you can easily integrate:
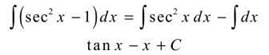
2. Another trigonometric substitution is needed in this problem. According to the Mamma Theorem, 1 — sin2 x = cos2 x. Therefore, the integral can be rewritten as
![]()
This is especially useful since the derivative of tan x is sec2 x, which prods you to use u-substitution. If u = tan x, du = sec2 x dx:
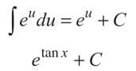
3. First of all, get the boundaries to match up. According to definite integral properties, ![]()
(a) ![]()
(b) Think about the graph of f(x) + 2 when compared to f(x). The graph is the same, only moved up two units. The effect is demonstrated by the diagram below:
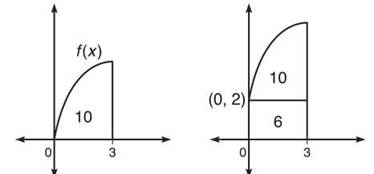
The new graph has an additional rectangle of area 6 (length 3 and height 2) beneath the original area of 10. Therefore, ![]()
4. If u = x-4, then du = —4x-5dx, so ![]() This u-substitution makes the integral
This u-substitution makes the integral
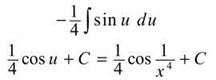
5. In order to find the average value, you’ll need ![]() Hopefully, your instinct is pushing you toward «-substitution. When integrating exponential functions, it’s best to set u equal to the entire exponential function, so
Hopefully, your instinct is pushing you toward «-substitution. When integrating exponential functions, it’s best to set u equal to the entire exponential function, so

That seems all well and good, but where is the “sec x tan x” in the original problem? Do you see it? Rewrite ![]() as
as ![]() and the original function becomes
and the original function becomes
![]()
Now it’s time to actually find the average value of v:
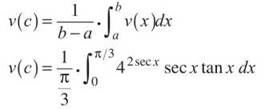
Now, do the u-substitution, as outlined above, to get
![]()
Don’t forget to get the new boundaries of 16 and 256 by plugging 0 and π/3 into the statement.
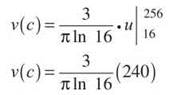
NOTE. If number 6 had asked for ![]() you would not have taken the opposite of the negative signed area between x = -1 and x = 5. The absolute value signs mandate that all of the signed area must be turned positive.
you would not have taken the opposite of the negative signed area between x = -1 and x = 5. The absolute value signs mandate that all of the signed area must be turned positive.
6. The graph of x2 — 4x — 5 without the absolute values is a concave-up parabola. To find the roots, factor and set each equal to zero. The roots are, therefore, — 1 and 5.
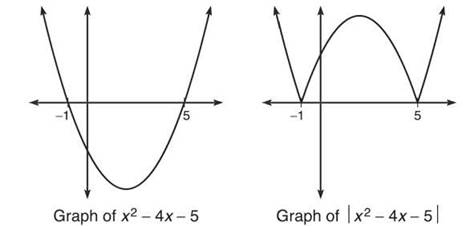
The graph of |x2 — 4x — 5| is the same, except that its negative portion flips above the x-axis, as the absolute value cannot have a negative output. Therefore, to find the area beneath the right graph above, we will find the area beneath the left graph and take the opposite of the area between —1 and 5 (since that area will be negative as it is below the x-axis).
![]()
7. You should use Fundamental Theorem Part Two. Plug in the upper bound, and multiply by its derivative to get j'(x):
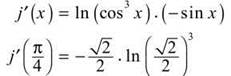
8. Find ![]() whatever you get must integrate to get the original expression. You don’t have to worry about the absolute value signs at all—they’re only there for the benefit of the In function.
whatever you get must integrate to get the original expression. You don’t have to worry about the absolute value signs at all—they’re only there for the benefit of the In function.
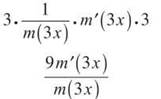
9. This problem was much easier if you memorized your trig integrals. First of all, you’d notice that tan x and its integral’s opposite, ln |cosx|, are both in the expression. Therefore, you should do a u-substitution with u = ln |cosx|. That makes du = —tan x dx, and —du = tan x dx. The integral now becomes
![]()
You’re not out of the woods yet! You still have to remember what the integral of sec u is. Are you thinking that you should have memorized those silly things? Do it now!
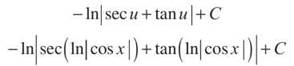
10. (a) Because the definite integral represents accumulated change, it gives you total sales (not total rate of sales or anything weird like that). If January 1998 = 0, then February 1998 = 1 and March 1999 = 15, and the correct definite integral is ![]()
(b) The average rate of change over the interval [0,18] is ![]()
(c) r(t) is the rate of change, or derivative, of the total sales function. Therefore, the total sales function will be concave up whenever r(t) is increasing, which is on the interval [0,12].
11. Use the Fundamental Theorem in order to evaluate the definite integral:
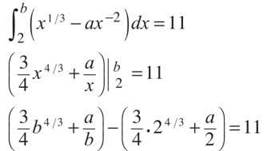
All that remains is to solve the equation for a:
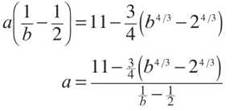
NOTE. Even though you are only given velocity values and not the actual velocity function, you are still approximating the area beneath the velocity function in 12(a) and (b). Therefore, we call that mystery function v(t) in 12(c), even though we don’t know what it is.
12. (a) We can assume that Dale stuck to the inner lanes as much as possible to cut down on his time, so you are basically finding the length of the innermost lane of the track, since the definite integral of velocity is distance traveled. Before you begin, you must standardize the units. Since the speed is in mph, you should transform the seconds into hours to match. For example, since there are 602 = 3,600 seconds in an hour, 10 seconds are equal to ![]() hours. If you convert all the times, the chart becomes
hours. If you convert all the times, the chart becomes
|
time(hrs) |
0 |
1/360 |
1/180 |
1/120 |
1/90 |
1/72 |
1/60 |
|
speed(mph) |
0 |
98 |
117 |
225 |
233 |
228 |
241 |
Using midpoint sums, the width of each interval will be 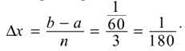 The midpoints of the intervals occur at t = 10, 30, and 50 seconds, or
The midpoints of the intervals occur at t = 10, 30, and 50 seconds, or ![]() and
and ![]() hours. Therefore, the midpoint sum is given by
hours. Therefore, the midpoint sum is given by ![]()
(b) The Trapezoidal Rule estimation for this problem is
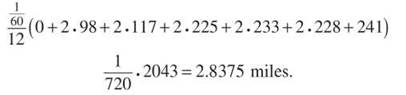
(c) Dale’s average speed is the average value of the velocity function. The fact that speed is the absolute value of velocity is irrelevant in this problem, as Dale’s velocity is always positive.
Average speed = 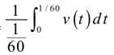
In part (b), you found that ![]() Plug this value into the average speed formula.
Plug this value into the average speed formula.
Average speed = 60 ∙ 2.8375 ≈ 170.250 mph
13. (a) Since position is the integral of velocity, you know that
s(t) = t3 — 5t2 + 15t + C
But, you also know that s(1) = 8, so plug that into the function to find C.
s(1) = 13 - 5 ∙ 12 + 15 ∙ 1 + C = 8
1— 5 + 15 + C = 8
C = —3
Therefore, the exact position equation is
s(t) = t3 — 5t2 + 15t — 3
(b) The distance traveled is not just ![]() That gives you the total displacement of the function. If the particle changes direction and comes back toward the origin, your answer will be wrong. For example, if the particle moves right 15 inches until t = 3 and then moves left 8 inches from t = 3 to t = 5, the definite integral above will give a result of 7 inches, whereas the particle really moved 15 + 8 = 23 inches. So, you have to make sure the particle does not change direction on [0,5]. How do you do that? Dust off the wiggle graph.
That gives you the total displacement of the function. If the particle changes direction and comes back toward the origin, your answer will be wrong. For example, if the particle moves right 15 inches until t = 3 and then moves left 8 inches from t = 3 to t = 5, the definite integral above will give a result of 7 inches, whereas the particle really moved 15 + 8 = 23 inches. So, you have to make sure the particle does not change direction on [0,5]. How do you do that? Dust off the wiggle graph.
s'(t) = v(t) = 3t2 – 10t + 15 = 0
Luckily, v(t) >0, and the particle never stops or turns backward (according to its graph). Therefore, the total distance traveled will be
![]()
In fact, because the particle never turns around, you could say that the total distance traveled is s(5) — s(0), where it stopped minus where it started, which is 78 — 3 = 75.
(c) The average velocity is the average value of the velocity function (most of which you’ve already figured out):
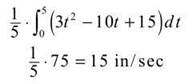
When is the particle actually traveling at a rate of 15 in/sec? Set the velocity equation equal to 15, and solve.
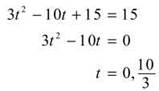
SUMMING IT UP
• The third major topic of calculus (limits and derivatives are the two) is integration or antidifferentiation.
• You can only pull coefficients out of integrals.
• Although the Power Rule for Integrals is relatively easy, it is also easy to make mistakes when the exponents are fractions or have negative powers. Be careful.
• If you ever wonder when to calculate area and when to calculate signed area, when computing definite integrals, it’s always signed area.