Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 8. Advanced Methods of Integration

POWERS OF TRIGONOMETRIC FUNCTIONS (BC TOPIC ONLY)

NOTE. This is not universally called the “Odd Man Out Rule,” so don’t refer to it as such on the test; this rule has no universally accepted name.

If we’ve done anything, we’ve done a lot of trigonometric integration, so here’s a little more to throw on the top of the pile. In this section, you learn a few more coping strategies for when all of our other methods fail. These methods, like others we’ve covered, often help out when w-substitution does not quite work out. The first of these is something I call the Odd Man Out Rule, and it works for sine and cosine.

Odd Man Out Rule: If an integral contains positive powers of sine and cosine, and only one of the powers is odd, keep one of the odd-powered factors and convert the rest to the other trigonometric expression using the Mamma Theorem. Is there anything your Mamma can’t do?

Example 8: Evaluate

Solution: In this integral, cos x is the odd man out, since it has the odd power of the two factors. Therefore, we want to leave behind only one cos x and convert the other cosines to sines (truly making cos x the odd man out).

The Mamma Theorem tells you that cos²x = 1 — sin²x, so replace the cos²x to get

Distribute the sin²x and the cos x to both terms, and split the integral to get

Now, you can perform u-substitution in each expression with u = sin x to get

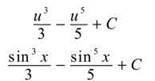
What if you have only sines or cosines in the problem and not both? In this case, you cannot count on the odd man out to help with u-substitution. If this occurs, you will have to resort back to the power-reducing formulas from way back in Chapter 2. Once applied, they make the problem almost a trivial pursuit.

Example 9: Evaluate

Solution: The power-reducing formula for sin²x is so you can substitute that into the integral and factor out 1/2.

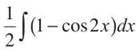
Split the integral up,

and use u-substitution (with u = 2x) to integrate cos 2x.

TIP. If the problem had contained sin x to an odd power, you would have left a sin x behind and converted the remaining sines to cosines using Mamma—the same procedure.

The final rule for trigonometric powers works for secants and tangents in the same integral. I call it the Steven and Todd Rule, since it has to do with secants being even and tangents being odd.

Steven and Todd Rule: If an integral contains positive powers of secant and tangent and the power of secant is even, save a sec²x and convert the remaining secants to tangents using Pappa. If, however, the power of tangent is odd, save a sec x tan x and convert the remaining tangents to secants using Pappa.

This might be the opposite of your first instincts. If you are focusing on an even power of secant, you are preparing a sec²x term, which is the derivative of tangent. If you are focusing on the odd power of tangent, then you are preparing a sec x tan x term, the derivative of secant. However backward it may seem, it works like a charm.

Example 10: Evaluate

Solution: Steven is in this problem, waving to you, eating a hotdog, and waiting until you see him (since secant is even). Therefore, you prepare a sec²x term and convert the remaining sec²x term to 1 + tan²x using Pappa.

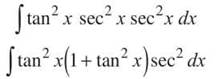
Distribute the tan²x sec²x, and split the integral to get

Use u-substitution with u = tan x to finish.

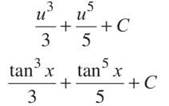
This answer looks hauntingly similar to Example 8, and that’s no real coincidence. Odd Man Out and Steven-Todd are techniques that set you up for a simple u-substitution and differ only in very minor ways.

There may be instances in which you cannot use any of the techniques outlined here. Do not panic. Try some old-fashioned elbow grease, and experiment until something works. Break the integral into smaller pieces, and bring Mamma, Papa, and Baby into the picture.

Example 11: Evaluate

Solution: No u-substitution is possible yet. If you set u = cos x, there’s no sine to help out on the du. So, let’s introduce a sine (or two) into the problem with Mamma.

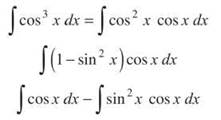
The left integral is easy, and the right integral is a simple u-substitution (u = sin x).

EXERCISE 3

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

EVALUATE THE FOLLOWING WITHOUT A GRAPHING CALCULATOR

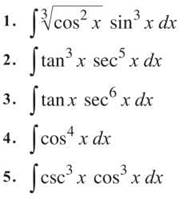
ANSWERS AND EXPLANATIONS

1. You need to use the Odd Man Out Rule for this integral (even though the cosine is to a weird power). Save a sin x, and transform the remaining sin²x to (1 — cos²x):

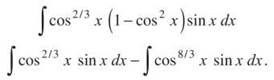
Both of these integrals require u-substitution with u = cos x (don’t forget that du = —sin dx).

2. It’s Todd (tangent is odd), so save a sec x tan x term and transform all the tangents to secants using Pappa.

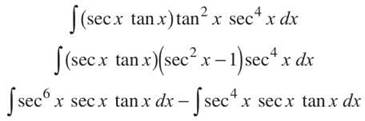
Now, use u-substitution with u = sec x to finish.

3. Both Steven and Todd are in this problem, so you can do the problem either way. However, Todd provides the easier way (since saving a sec x tan x term leaves no other tangents to transform to secants). Bring it home, Todd.

Use u-substitution with u = sec x (just as in number 2).

4. There is no sine in this problem to help with u-substitution. So, do we use the technique of Example 9 or Example 11? Because the power is even, we’ll use the technique of Example 9, where the power also was even.

Now, use the power-reducing formula for cos²x.

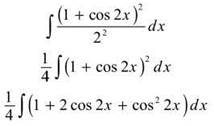
The first two integrals are easy, but you have to use another power-reducing formula for cos 2x. Let’s focus on that for a moment. (Don’t forget the 1/4 that needs to be distributed to each integral—easy and hard alike.)

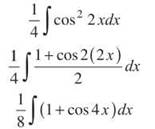
All together (don’t forget the two easy integration terms above), the answer is

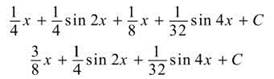
5. Holy smokes, this doesn’t match a single one of the techniques we’ve covered! To begin, rewrite as sine and cosine to see if things get any easier.

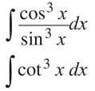
That looks a little more compact, if nothing else. This, however, looks a lot like Example 11; in fact, it differs by only a single letter. Try that technique on a whim, and see what pans out.

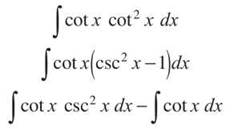
The left integral is a u-substitution, and you should have the right integral memorized.