Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 8. Advanced Methods of Integration
TECHNOLOGY: DRAWING DERIVATIVE AND INTEGRAL GRAPHS WITH YOUR CALCULATOR
In past chapters, you were asked to describe characteristics of functions based on the graphs of their first and second derivatives. Your calculator (although slow) is able to draw a function’s derivative or integral graph, even if you cannot figure out what it is. This is not an extraordinarily useful tool for the AP test, but it gives you an infinite amount of practice drawing the graphs of derivatives and integrals (and solving each one for you).
Example 17: Draw the graphs of ∫cos x dx and ![]()
Solution: You already know what the integral of cos x is—it’s sin x. However, the process you use with any function will be the same. Before we begin, let’s set up a good [Window] for this problem. Press [Zoom] → “Ztrig”, and then adjust the [Window] so that “Xmin” is 0 and “Xmax” is 4π. This will set up a very pretty window for cos x. Now, go to the [Y=] screen and assign Y1 = cos (x). We want Y2 to be the graph of the integral, so its equation is
![]()
NOTE. This chapter doesn’t need a specific technology component, so an unrelated but important calculator topic is included.
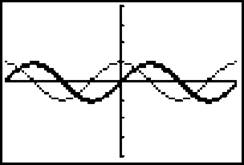
This is the area beneath the Y1 curve with respect to x from x = 0 to x = whatever the current x is. In other problems, you may want to adjust the lower limit of integration (in this example 0) to match the “Xmin” value on your graph.
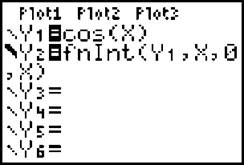
It’s also a good idea to darken the graph of the integral so you can tell them apart. Press [Graph], wait a bit, and the graph of the integral slowly scrawls itself across the axes. No big surprise here; it’s the graph of sin x, the integral of cos x.
NOTE. In order to get Y1 into the equation of Ysb2, press [Vars] → “Y-vars” → “Function...” → “Y1”.
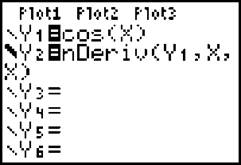
If you want to draw the derivative of cos x, enter
![]()
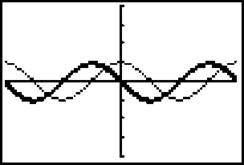
Just as we suspected, the graph of the derivative of cos x is the horizontal reflection of sin x, or —sin x.
If you are still confused about the relationship between a graph and its derivatives, this technique can give you all the practice you need. Make up any function at all, and enter it as Y1. Predict, based on that graph, what its integral and derivative graphs look like, and use the above commands to check yourself.
Example 18: Show that ln x gets its value by accumulating area beneath 1/x.
Solution: Enter Y1 = 1/x. Remember that In x gets its value from the accumulation function
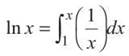
So, ![]() Make sure to set your Xmin to a number slightly larger than 0 (since 0 is undefined for 1/x). I chose a value of .001 for Xmin.
Make sure to set your Xmin to a number slightly larger than 0 (since 0 is undefined for 1/x). I chose a value of .001 for Xmin.
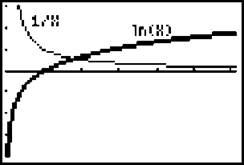
This activity sheds a whole new light on why In x is negative from x = 0 to x = 1 : ln x is based on an integral with inverted limits of integration on that interval. For example,
![]()
Because those limits are “backward” (with the larger limit in the lower position), the result is negative (based on a property of definite integrals).
EXERCISE 6
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
DO NOT USE A GRAPHING CALCULATOR ON A SINGLE, SOLITARY ONE OF THESE PROBLEMS
Evaluate each of the following integrals, if possible.
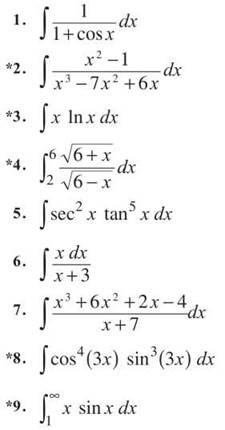
*10. James’ Diabolical Chalienge: ![]()
*a BC-only question.
ANSWERS AND EXPLANATIONS
TIP. Although no one integration method is extremely difficult, it can be tricky trying to decide which one to use. Make sure you know why and when to use the methods you’re using.
1. The best way to integrate this is using a method called the conjugate. It hasn’t been included until now because it is much easier than the other methods. To apply it, multiply the numerator and denominator by the conjugate of the denominator (1 — cos x); you will get
![]()
Use Mamma to change the denominator and split the integral into two parts.
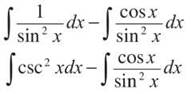
The first integral is easy, and the second is a simple u-substitution (with u = sin x).
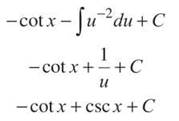
2. This is not a long-division problem because the degree of the denominator is greater than the degree of the numerator. Instead, because the denominator is factorable, you should use partial fractions.
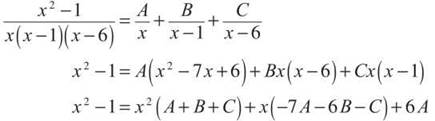
Therefore, A = —1/6, B = 0, and C = 7/6. The integral is now written as
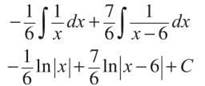
3. Integration by parts is the way to go here. It’s best to set u = ln x; although you probably have memorized its integral, you’d have to integrate twice if you set dv = ln x, so that rules out the chart. Instead, set u = ln x and dv = xdx, which makes ![]() and
and ![]()
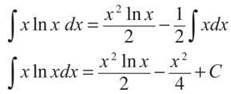
4. (This is a toughie.) This is an improper integral since the boundary of 6 wreaks havoc in the denominator.
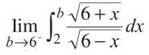
The best method to use is the conjugate method (since the denominator is a radical surrounding a binomial). Multiply the top and bottom of the fraction by ![]() to get
to get
![]()
This integral must be broken into two parts. We’ll solve them one at a time. The first is

The second integral is completed using u-substitution.
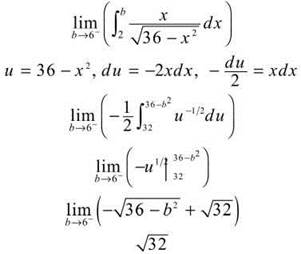
The final answer is the sum of the two integrals:
![]()
5. This is a simple u-substitution problem; BC students can also use Steven or Todd (although Steven, in this case, is essentially u-substitution).
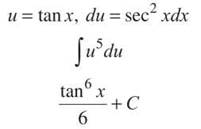
6. There are two good ways to do this. If you use long division (since the degrees of top and bottom are equal), you get
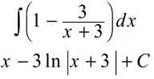
which is quite easy. You can also do a bizarre u-substitution. If you set u = x + 3, du = dx and the integral becomes
![]()
How do you get rid of that pesky x in the numerator? Remember that you just set u = x + 3. Therefore, x = u — 3. If you substitute that value in for x, you get
![]()
which can be split up, resulting in
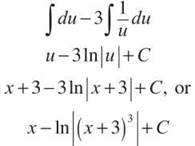
(since the 3 is just a constant and can be added to the C). Both methods result in the same answer.
7. You need to begin this problem with long or synthetic division (synthetic division is shown below).
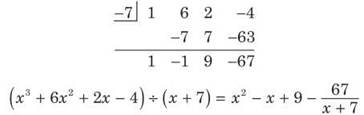
The integral can be rewritten as
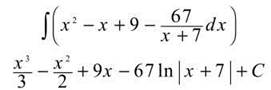
8. The odd man out in this problem is sin (3x). Therefore, save one sin (3x), and change the others to cosines.
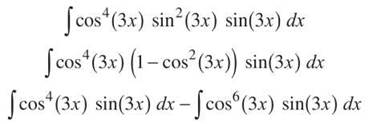
Both integrals require u-substitution with u = cos (3x) and ![]()
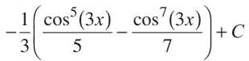
9. This is an improper integral due to the infinite upper limit.
![]()
You should integrate x sin x by parts with u = x and dv = sin x dx. In fact, you can use the parts chart.
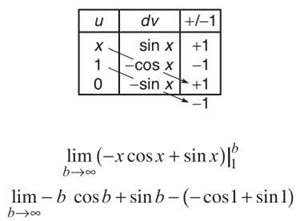
As b approaches infinity, neither cos b nor sin b approaches any one height. They both oscillate infinitely between —1 and 1. Therefore, there is no limit as b approaches infinity, and this integral diverges.
10. This is one mother of an integration by parts problem. If you don’t use the chart, you are just masochistic.
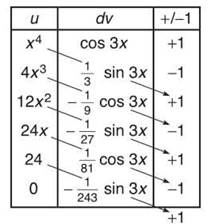
Multiply along the diabolical diagonals (and simplify fractions, if you feel the urge) to get the final answer:
![]()
SUMMING IT UP
• Most of integration on the AP test is done using the Power Rule and u-substitution.
• Integration by parts is a technique based on the Product Rule (BC topic only).
• When you integrate by partial fractions on the AP test, the denominators will always have linear factors. This technique is slightly modified when the factors have higher degrees, but you don’t have to worry about that for the AP test.
• Improper integrals are integrals that have the following qualities: one of the limits of integration is infinity and the curve being integrated has an infinite discontinuity between the limits of integration (BC topic).
• Not all shapes with infinite boundaries have finite area. If the area is not finite, the integral is said to diverge, whereas a finite integral is said to converge.