Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 2. Calculus Prerequisites
INVERSE FUNCTIONS
NOTE. Plugging one function into another is called composing the function with another. It it usually written as f(g(x)), where the function g is being plugged into f. The notation (f° g)(x) is also used; it means the same thing.
Everything has its eventual undoing—for every high there is a low, and for every up, there is a down. The specific element that actually plays the role of spoiler depends on the situation, of course; Superman has kryptonite and the Wicked Witch of the West has the bucket of water. Functions are no exception to this rule—every function, f(x), has its inverse function, f-1(x)—a rule that completely “undoes” the function, effectively destroying it, leaving behind only a smoldering, wide-eyed variable. This is a little too much imagery for most mathematicians, who choose, instead, to write f(f-1(x)) = f-1(f(x)) = x. Translated, this means that any function of x, when plugged into its inverse function (or vice versa), leaves behind only x.
Any functions that satisfy this condition are inverse functions. Some inverse functions are pretty obvious. For example, the inverse of g(x) = x + 3 is a piece of cake: g-1(x) = x — 3. (The opposite of adding 3 to a number is subtracting 3). Flowever, it’s not always so obvious to determine if functions are inverses of each other.
Example 9: Prove that h(x) = 2x2 — 3, x ≥ 0 and 
are inverse functions.
Solution: If the functions fit the above rule, they are inverse functions, but if the glove don’t fit, we must acquit.
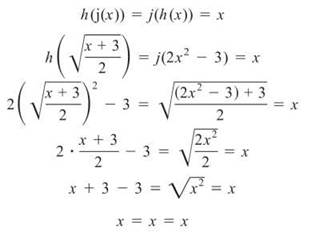
NOTE. We must restrict h (x ≥ 0) to ensure that it has an inverse function. This is explained later in this section.
Therefore, h and j are inverses.
You may be wondering how functions and their inverses actually “undo” each other, as we have said. The answer is that, in essence, inverse functions reverse the domain and range of the “host” function, making the inputs the outputs and the outputs the inputs. Consider the simple function r: {(1,5),(2,—3),(7,1/2),(9,2π)}. Clearly, the domain is {1,2,7,9} and the range is {5,—3,1/2,2π}. It is quite easy to construct r-1—simply switch the domain and range: r-1: {(5,1),(—3,2),(1/2,7),(2π,9)}. Now, the defining property of inverse functions becomes more obvious. Consider r-1 (r(x)) for the ordered pair (1,5). Because r(1) = 5, we write r-1(r(1)) = r-1(5) = 1. You end up with a 1, just as you started, and the functions have, in essence, canceled one another out. The same property is at work when you commute from home to school in the morning and then back home in the afternoon. The rides to and from school are inversely related, and you end up back where you started.
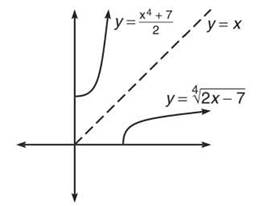
Because the purpose of inverse functions is to reverse the domain and range of a function—changing the order of the function’s (x,y) pair— the graphs of inverse functions have a special property as well. The graphs of inverse functions are reflections of one another across the line y = x. Below, the functions h and j from Example 9 are graphed. Notice how they are symmetric to each other across the y = x line.
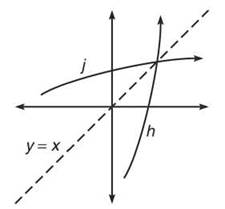
h and j are symmetric about y = x.
NOTE. By restricting the graph of h to x ≥ 0, you are removing the left half of the parabola. The resulting graph only increases from left to right, as the portion that decreased was included on x < 0. Because the restricted graph moves only in one direction, it is termed monotonic. Many monotonic graphs have inverses because of their unidirectional nature.
It’s worth discussing why you had to limit the domain of h in order to even qualify h for an inverse function. The graph of h(x) = 2x2 — 3, with no restriction, has two roots.
Easily found, the two roots are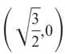 
and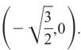 
Because inverse functions reverse ordered pairs, h-1 must include the points 
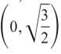and 
If this were allowed, h-1 would have two outputs for the domain element 0 and, therefore, could not be a function.
The visual test used to ensure that a function has an inverse is called the horizontal line test, and it works much like the vertical line test. If any horizontal line drawn through a function graph intersects the graph at more than one place, the function cannot have an inverse. (In the function h above, because the parabola has two roots, the horizontal line y = 0 intersects the parabola in two places—one of many such lines that ensures h fails the test.) If a function passes the horizontal line test, it is said to be one-to-one. In other words, for every input there is one output and vice versa.
It still remains to actually find an inverse function, but the process is rather simple and is directly based on the properties dicussed above.
Example 10: Find the inverse function of 
Solution: Because inverse functions, in effect, switch the x and y variables, do so in the function, and solve the resulting equation for y. This is the inverse function.
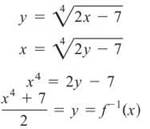
However, you must restrict f-1(x) to x ≥ 0 to make the graph monotonic and ensure the existence of an inverse.
EXERCISE 3
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR ALL OF THESE PROBLEMS.
1. If f(x) = x2 + 3x +1 and 
find
(a) (f° g)(x)
(b) g(g(x))
(c) g-1(f(x))
(d) g(f(4))
USE THE CHART BELOW FOR PROBLEMS 2 AND 3.
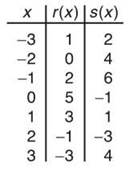
2. If r(x) and s(x) are functions, as defined above, evaluate
(a) r(s(2))
(b) s(r-1(0))
(c) r-1(r-1(s(1)))
3. Why does s-1(x) not exist?
4. Find the inverse functions of each (if possible):
(a) p(x) = 2x3 — 1
(b) y = [[x]]
5. If h(x) = x5 + 3x — 2, find h-1(4).
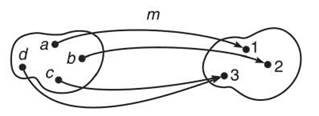
6. Using the definition of one-to-one functions, explain why function m, as defined in the function map below, has no inverse.
ANSWERS AND EXPLANATIONS
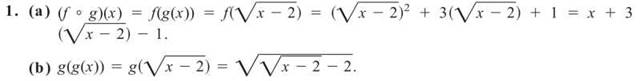
(c) First, find g-1(x). Using the same method as Example 10, g-1(x) = x2 + 2. Now, g-1(x2 + 3x + 1) = (x2 + 3x + 1)2 + 2 = x4 + 6x3 + 11x2 + 6x + 3.
(d) Clearly, f(4) = 29 (by substitution), so 
2. This problem is simplified by finding r-1(x) (by reversing the ordered pair of r); r-1: {1,-3), (0,-2), (2,-1), (5,0), (3,1), (-1,2), (-3,3)}.
(a) r(s(2)) = r(-3) = 1.
(b) s(r-1(0)) = s(-2) = 4.
(c) r-1(r-1(s(1))) = r-1(r-1(1)) = r-1(-3) = 3.
3. Function s has no inverse because it is not one-to-one. Notice that both x = —2 and x = 3 result in the same output of 4. In a one-to-one function, every output must have only one input that maps to it.
4. (a) Reverse the x and y to get x = 2y3 — 1, and solve for y; 
(b) There is no inverse function for y = [[x]] since the greatest integer function fails the horizontal line test. Because the graph is a collection of horizontal line segments, a horizontal line overlapping one of these segments will intersect an infinite amount of times.
5. This problem is difficult because you cannot find h- (x)—if you try to use the method of Example 10, you are unable to solve for y. Thus, a different approach is necessary. Note that if 4 is in the domain of h-1 (as evidenced by the fact that we are able to plug it into h -1), then it must be in the range of h. Thus, h-1 contains some point (4,a) and h contains (a,4), where a is a real number. Substitute the point (a,4) into h to get a5 + 3a — 2 = 4, and use your graphing calculator to solve the equation. Therefore, a = 1.193 and h-1 contains the point (4,1.193). Flence, h-1(4) = 1.193. See the technology section at the end of this chapter to review solving equations with the graphing calculator.
6. Notice that m(c) = m(d) = 3. Therefore, two inputs result in the same output, m is not one-to-one, and only one-to-one functions can have inverses. One-to-one functions map one domain element to one range element; visually, this means that only one road can lead away from each input and only one road can lead into each output.