Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 9. Applications of Integration
THE DISK AND WASHER METHODS
My students are always surprised when I tell them that calculus can help them find the volume of a butternut squash. However, when they see how it’s done, they are often disappointed. “That’s not calculus!” they exclaim. “Is too!” I cleverly retort. “Is not !”they protest. Such academic debates are essential to producing enlightened and well-spoken students.
There is no formula in your textbook concerning the volume of produce, so you need to break the squash into smaller, more manageable pieces.
A squash’s cross-section
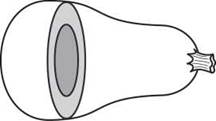
If you slice the squash into thin disks (cylinders), you can find the approximate volume of each and then add those volumes. Sound familiar? It’s basically a three- dimensional Riemann sum.
The volume of a disk is πr2h. However, if we want to find the exact volume of a three-dimensional shape, we have to use an infinite number of disks (like we used an infinite number of rectangles to find the exact area when we applied the Fundamental Theorem). This formula is called the Disk Method.
The Disk Method: If the area beneath a function is rotated in three dimensions and the resulting solid has no holes or gaps, its volume is given by
where a and b are the endpoints of the original area and r(x) is the radius of the three-dimensional solid.
This sounds mighty complicated, but it is really quite simple. (And that’s no typical math teacher mumbo jumbo.) One thing to keep in mind: The Disk Method uses rectangles that are perpendicular to the rotational axis. If you remember that, the process is much simpler.
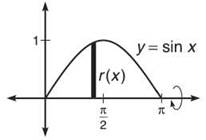
Example 1: Find the volume generated if the region bounded by f(x) = sin x on [0,π] is rotated around the x-axis.
Solution: Draw the original region first (you don’t have to be able to picture it in three dimensions to get the problem right.) The x-axis (the rotational axis specified by the problem) is horizontal, so we will have to use rectangles perpendicular to that (vertical rectangles) to complete the problem. Remember from the last section that vertical rectangles mean that everything is in terms of x.
ALERT! Don’t forget to multiply by the π outside the integral.
To find r(x), just draw one sample vertical rectangle on the interval. How do you find its height? Use top — bottom like we did in the last section. So, r(x) = sin x — 0. According to our formula, the volume of the resulting solid will be
AB students will have to use their calculators to integrate this, but BC students should be able to do it by hand. The answer is π2/2 or approximately 4.935.
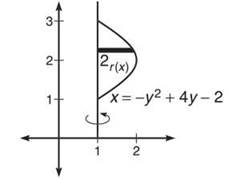
Example 2: Find the volume of the region bounded by x = —y2 + 4y — 2 and x = 1 rotated about the line x = 1.
Solution: This time, the rotational axis is vertical, so you have to use horizontal rectangles (which should be very easy, since the function is already in terms of y). All you have to do is find a, b, and r(y) and plug them right into the formula. The endpoints are y = 1 and y = 3 (they have to be y values). Once again, you can draw a sample rectangle in order to find the radius.
NOTE. The Disk Method is the same for horizontal rectangles, except a and b are now y endpoints and the radius is in terms of y, not x.
To find length with horizontal rectangles, you take right — left, so the radius is given by (-y2 + 4y - 2) - 1.
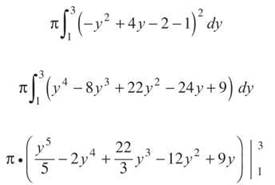
The rotational volume is 16π/15, which is much prettier an answer than you thought it would be, isn’t it?
Sometimes, rotational solids aren’t all that solid. Consider the region bounded by the horizontal lines y = 1 and y = 2 on the interval [0,3].
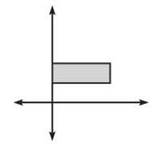
If this figure is rotated about the v-axis, the empty space between y = 0 and y = 1 gets rotated, too, creating a three-dimensional doughnut. The more practical-minded mathematicians of the days of yore thought it looked more like a washer (hence the name Washer Method).
NOTE. You can also use the Washer Method with y’s by adjusting the same way you did with the Disk Method.
The Washer Method works the same way as carving a pumpkin for Halloween. If you want to find the volume of a jack-o-lantern, what would you have to do? First, you’d have to find the volume of the whole pumpkin (including pumpkin guts). Second, you’d have to find the volume of the hollowed-out space inside the pumpkin and subtract that from the original volume (sort of like the shaded area problem in the beginning of this chapter). In the Washer Method, you use the Disk Method twice, once to find the overall volume and once to find the volume of the hole.
The Washer Method: The rotational volume of the area bounded by two functions, f(x) and g(x), on [a,b] if f(x) ≥ g(x) on [a,b]) is given by
where R(x) is the outer radius (the radius of the outer edge of the region) and r(x) is the inner radius (the radius of the hole of the region).
Again, this method looks insanely difficult, but it is not bad if you’ve been paying attention since the beginning of this chapter.
NOTE. Use rectangles perpendicular to the rotational axis with the Washer Method, just like you did with the disk. Washer = perpendicular. Remember that both words growl at the end (just like you do after you eat chili).
Example 3: Find the volume generated by revolving the area bounded by the curves y = √x + 1, x = 4, and y = 1 about the x-axis.
Solution: If you rotate the given area around the line y = 1, there is no hole in the rotational solid. However, since you are revolving around the line y = 0, there is a gaping hole there.
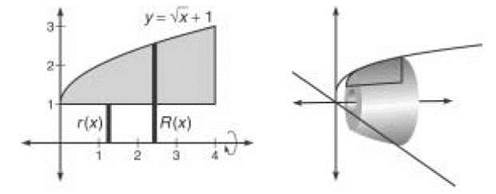
We are using vertical rectanges, since the axis of revolution (the x-axis) is horizontal. Notice that the outer radius, R (x), reaches from the axis of rotation to the outer edge of the region. The inner radius, r(x), reaches from the axis of revolution to the outer edge of the gap between the region and the axis. You can find the length of each by subtracting top — bottom:
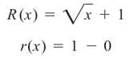
ALERT! Don’t forget to square the radii in the Disk and Washer Methods; the formula is based on πr2, as you saw at the beginning of the section. I forget to square all the time—don’t let yourself get into the habit.
The boundaries of the region are x = 0 and x = 4. Throw all these components together, and you get the volume according to the Washer Method:
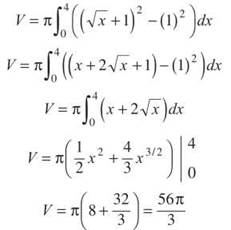
EXERCISE 2
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 4 AND 5.
1. Find the volume generated by revolving the area in the first quadrant bounded by y = x2 and x = 3 about the line x = 3.
2. True or False: If 
then the volume generated by revolving each of those regions about the x-axis is equal. Give an example that supports your position.
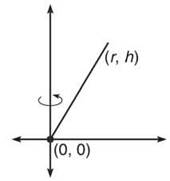
3. If you rotate the line segment below about the y-axis, you get a right circular cone of height h and radius r. Verify that the cone has a volume of 
4. Find the volume, V, generated by revolving the region bounded by y = (x + 2)3, y = 0, and x = 0 about x = 1.
5. Find the volume, V, generated by revolving the region bounded by y = tan x, y = 0, and π/4 about the x-axis. Then, find the value of c on [0,π/4] such that a plane perpendicular to the x-axis at x = c divides V exactly in half.
ANSWERS AND EXPLANATIONS
1. Because you are revolving about a vertical axis, you need to use horizontal rectangles. With such rectangles, everything must be in terms of v, so you have to rewrite y = x2 as x = √y.
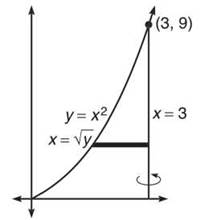
The length of the example rectangle is given by right — left, or 3 — √y. Therefore, the volume is
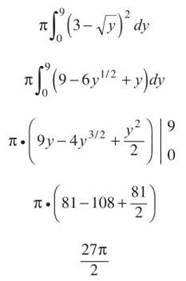
2. The problem proposes that two regions of equal area result in the same volume once rotated about the x-axis. This is false. Consider the two regions pictured below, both of area 1.
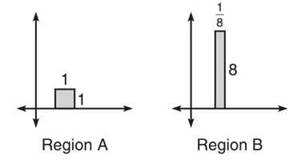
Both revolutions are solid disks with known radii and heights, so we can apply the formula V = πr2h to find their volumes. The solid of revolution generated by region A has height = 1 and radius = 1; the volume is π. Region B generates a disk of height 1/8 and radius 8; its volume will be π ∙ 82 ∙ 1/8 = 8π. The volumes are very different.
NOTE. In problem 3, remember that h and r are constants; treat them like numbers.
3. To start, you need to find the equation of that line segment. Because it passes through (0,0) and (r,h), it has slope h/r and y-intercept 0. Thus, the equation is
However, you are revolving about a vertical axis, so the rectangles need to be horizontal, and the equation needs to be in terms of y:
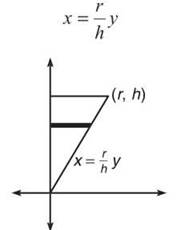
Therefore, the volume generated after revolution will be
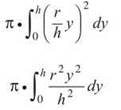
You can pull out the constants to simplify the integral.
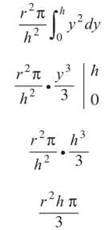
4. This solid of revolution will have a hole in it, so you have to use the Washer Method. Again, a vertical axis of revolution means horizontal rectangles. Therefore, the function must be rewritten as 
The inner radius (from the axis of revolution to the outside of the region) is 
and the outer radius (from the axis of revolution to the outside of the hole) is 1 — 0 = 1.
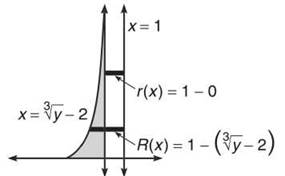
Therefore, the volume is
You might as well use your calculator to find the answer. You should know how to use the Fundamental Theorem by now.
5. Finally, a problem in which we don’t have to convert the function in terms of v! Vertical rectangles are perpendicular to the x-axis, so the volume, V, will be
We can integrate tan2x by hand if we replace it with (sec2x — 1) using Pappa. However, save time by using your calculator since it’s allowed on this problem.
V ≈ .6741915533
We want to find a revolutionary volume that is exactly half of that, so we should set up this equation:
Unless you have a symbolic integrator (like a TI-89), you’ll have to integrate the left side by hand.
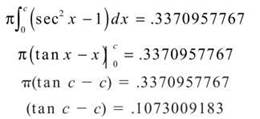
Use your calculator to solve this equation; you get
c ≈ .645