Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 10. Differential Equations
EULER’S METHOD (BC TOPIC ONLY)
If you could solve all differential equations using separation of variables, the world would be a much happier place. However, only a very small portion of differential equations can be solved that way. There are a slew of other methods you’d have to learn to become Supreme Ruler of Differential Equations, but luckily you don’t have to. Enter Euler, famous Swiss mathematician, and his method of fin ding approxim ate solutions to nonintegrable differential equations. Even though Euler’s Method only uses tangent lines and is quite simple in premise, you can use it to find an approximate answer to a differential equation.
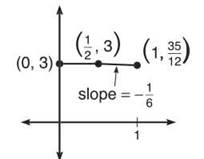
Before we dive into Euler’s Method, we need to focus on one simple concept. Let’s say that a line has slope 12/7 and contains point (1,0). If you start at the point and go 1/2 unit to the right, how many units must you go up to stay on the line? What y-coordinate completes the point on the following page?
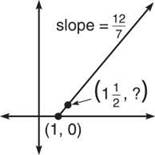
Believe it or not, the answer is quite easy. Take the slope formula that you’ve used since elementary algebra: m = ∆y/∆x. Solve it for ∆y.
∆y = m ∙ ∆x
In our line problem, the slope is 12/7, and the change in x (∆x) from (1,0) is 1/2. Plug these values into the new formula.
This tells you that the point (1/2,6/7) is also on the line with slope 12/7 and point (1,0). If you went 1/2 unit right of (1,0), you’d have to go 6/7 unit up to stay on the line. This is a very important part of Euler’s Method, although most textbooks do not explain what it means or why it is so important. Now, let’s map out the goal of Euler’s Method.
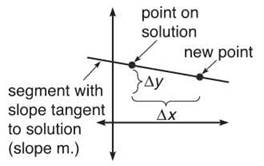
A typical differential equation contains a derivative and a point through which the solution graph passes. We will find the slope, m1, of the tangent line at that starting point. Then, we will travel a fixed distance right or left (∆x) and use the method above to find the corresponding ∆y. Basically, we are finding another point on the tangent line we just drew.
TIP. You will use your calculator a lot in Euler’s Method. Although you should learn to do the process by hand, you can use the calculator program in the back of this chapter to check your work.
This works because a tangent line has values close to the graph it’s tangent to (around the point of tangency). Once we find that new point, we repeat the process and find yet another point until we reach our approximation. The problem will typically tell you how many steps you should take to reach the solution, and (just like integration) the smaller the steps you take, the more accurate your answer. This probably sounds very complicated, but it’s quite easy. How many licks does it take to get to the Tootsie-Roll center of Euler’s Method? Let’s find out.
Example 1: Use Euler’s Method to approximate y(1) if 
and y(0) = 3. Use two steps of length ∆x = .5 when finding the solution.
Solution: This is the same differential equation we have seen numerous times now. We already know that its solution is a circle with radius 3, but let’s pretend we don’t, since most differential equations using Euler’s Method will not be solvable. We will have to repeat the method two times, once when x = .5 and once when x = 1 (since we are taking two steps of length — along the x-axis from x = 0 to x = 1, as the problem indicates).
What is the slope of the tangent line to the solution curve at (0,3)? Plug the values into dy/dx.
We will move 1/2 unit to the right along the tangent line (since ∆x = 1/2); in order to stay on the line (since it is horizontal), we should move neither up nor down. Our new point will be (1/2,3). It’s sort of like tightrope walking toward the solution—the tightrope is horizontal, and we edge our way 1/2 unit to the right along the high wire and stop there.
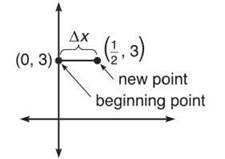
Now, repeat the process with the point (1/2,3). The slope of the tangent line here will be
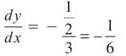
Again, we will move 1/2 unit to the right along this new tangent line. However, how much should we go up or down to stay on the new tangent line? Use the formula from the beginning of the section.
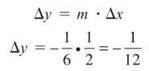
Therefore, the new point is 
and we’re finished.
Our approximation for f(1) is 35/12. Since we already know the actual solution of the differential equation is v2 + y2 = 9, we can find the actual solution of √8 ≈ 2.828427. Our estimate (35/12) is approximately 2.916667, so the approximation has an error of .08824.
Had we used more than two steps (which means a smaller ∆x) in Example 1, the answer would have been even more accurate. In the next example, we’ll use four steps to travel the same distance. Furthermore, you won’t be able to solve Example 2 by separation of variables. You’ll be out in the wild, untamed forest with only one weapon—Euler’s Method. Make sure you know how to use it!
Example 2: Approximate the value of y(2) for the differential equation 
using four steps of length ∆x = 1/4, given that the point (1,2) is on the solution curve.
Solution: We will have to repeat the process four times. If you want to use decimals instead of fractions, that’s okay, but remember not to round off until the very end. However, fractions will give you the exact answer—and don’t be shy about your calculator’s ability to add, subtract, and multiply fractions faster than you can.
Point (1,2): The slope of the line tangent to the solution is 
The corresponding ∆y will be
The new point will be 
Point 
The corresponding ∆y will be
The new point will be 
Point 
The corresponding ∆y will be
The new point will be 
Point 
The corresponding ∆y will be
The new point will be 
Therefore, your approximation of 
There you have it—Euler’s Method is quite mechanical, and besides the ugly fractions and/or decimals, it is a very handy way to approximate solutions to differential equations that we, as elementary calculus students, can solve no other way.
EXERCISE 3
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR TO SIMPLIFY YOUR ARITHMETIC FOR ALL PROBLEMS, BUT DON’T USE THE EULER’S METHOD CALCULATOR PROGRAM UNTIL PROBLEM 4.
1. Use Euler’s Method to approximate y(6) for 
given that y(5) = 2. Use three steps of size ∆x = 1/3.
2. (a) If the points (1,3) and (4,c) are on the solution graph to 
approximate c using Euler’s Method and three steps of length ∆x = 1.
(b) What limitations are evident in this approximation?
3. (a) Use Euler’s Method to approximate y(—1/2) for 
(where a is a real number) if y(0) = —2. Use two steps of length ∆x = 1/4.
(b) What is the error on your approximation if a = 3?
4. Approximate y(0) using 10 steps of length ∆x = .1 for 
given that y(—1) = 1. Fill out the chart below; it will help organize your information.
5. Give an example of a differential equation for which Euler’s Method gives the exact value rather than just an approximation.
ANSWERS AND EXPLANATIONS
1. The given point is (5,2) and ∆x = 1/3. We’ll start there and apply Euler’s Method three times.
Point (5,2): 
The corresponding ∆y is
The new point will be 
Point 
The new point will be 
Point 
The correct approximation for y is 
2. (a) This question is just asking you to find y(4) given a starting point of (1,3) and three steps of length 1 to get there.
Point (1,3): 
The new point will be (1 + 1, 3 + 4) = (2,7).
Point (2,7): 
The new point will be 
Point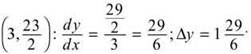 
Therefore, 
(b) The y-value is changing pretty dramatically as the x-value only changes by 1. With such a huge change in y, the approximation can’t be very accurate; it turns out to be within about 1 unit of the correct answer, but that is not nearly as accurate an approximation as you can get with a less steep graph. Of course, you can always increase the number of steps by decreasing ∆x; that will always make your approximation more accurate.
NOTE. Check out the slope field for 
It’s pretty.
3. (a) This one has only two steps, thank goodness. We will be stepping backward from x = 0 to x = —1/2, so ∆x must be negative: ∆x = —1/4.
Point (0,—2): 
The new point will be 
Point (—1/4,—2): 
The new point will be 
Therefore, Euler’s Method gives an approximation of —2 —a/8. The number a could be anything, so leave it as a.
(b) If a = 3, you have the equation 
our work above gives an approximation of 
To find out the actual value of y(—1/2), you have to solve dy/dx using separation of variables:
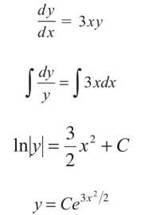
Plug in the given point (0,—2) to find C:
—2 = C ∙ 1
The solution equation will be 
its value for x = —1/2 (which we predicted to be —2.375) is actually
The error in the approximation was about .535.
4. The correct approximation for y(0) is nearly 6.129.
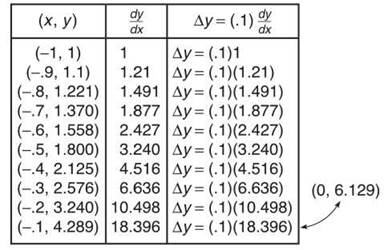
Note: 3 decimal places are written, but decimals are not rounded in calculations
5. If dy/dx = c, where c is any real number, the solution to the differential equation is just a line. Because Euler’s Method gets its value from the tangent line (and the tangent line to a linear equation is just the line itself), you will be stepping through the graph of the solution during Euler’s Method, and the answer will be exact. Try it, and see for yourself. Pick a value for c and a given point through which the solution line will pass; use Euler’s method to approximate something, and then double check it with separation of variables. The values will match.