Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 2. Calculus Prerequisites
HANDS-ON ACTIVITY 2.1: TRANSFORMING FUNCTIONS
The process of graphing functions becomes much easier once you can see how the presence of additional numbers affects a graph. You can move, reflect, and stretch a graph simply by tinkering with the constants in a function, as you will learn in this activity. You will find Hands-on Activities like this throughout the book. Sometimes, the best way to learn something isn’t by reading but by doing. In such cases, we have foregone notes and substituted these laboratory activities. In order to complete this activity, you will need to be able to graph functions on a calculator.
TIP. In the Hands-On Activities in this book, exact graphs a re not important. It is more important to get the general shape of the graph correct and pay more attention to the concepts behind the actvities instead.
1. Draw the graphs of y = x2, y = x2 — 1, and y = x2 + 2 on the grids below. The first you should know by memory (as one of the nine important functions described earlier in the chapter). You should graph the others with your graphing calculator.
2. How do the numbers —1 and 2 seem to affect the graph of x2?
_________________________________________________________
_________________________________________________________
3. Complete this conclusion: When graphing the function f(x) + a, the a value causes the graph off(x) to
_________________________________________________________
_________________________________________________________
4. Using the same process as you did for problem 1 above, graph the functions y = x3, y = (x — 3)3, and y = (x + 1)3.
5. How do the numbers —3 and 1 seem to affect the graph of x3?
_________________________________________________________
_________________________________________________________
6. Complete this conclusion: When graphing the function f(x + a), the a value causes the graph of f(x) to
_________________________________________________________
_________________________________________________________
7. Try to draw the graphs of y = (x + 2)2 — 3 and y = (x — 1)3 + 1 below, based on the conclusions you made in problems 3 and 6. Check your result with your graphing calculator.
8. Graph the functions y = |x + 1| and y = —|x + 1| below. You should be able to graph the first, but use the graphing calculator for the second.
TIP. You may need to consult your owner’s manual if you’re not sure how to graph absolute values on your calculator. On a H-83, the command is abs (and is found on the Math→Number menu.
9. Complete this conclusion: Multiplying f(x) by a negative, —f(x), causes the graph to
_________________________________________________________
_________________________________________________________
10. Graph the functions y = √x and y = √—x below, again using your graphing calculator for the second graph.
11. Complete this conclusion: Substituting —x into the function f(x) causes its graph to
_________________________________________________________
_________________________________________________________
TIP. When checking the second graph in Question 12 with your calculator, make sure you enter the function as ![]() If x - 1 is not in parentheses, the calculator interprets the equation as
If x - 1 is not in parentheses, the calculator interprets the equation as ![]()
12. Try to draw the graphs of y = —|x + 2| + 3 and ![]() based on all of your conclusions so far. Once again, check your results with your graphing calculator.
based on all of your conclusions so far. Once again, check your results with your graphing calculator.
13. Graph the functions y = x2 — 2 and y = |x2 — 2| on the grids below, again using your calculator only for the second graph, if possible.
14. Complete this conclusion: The graphs of/(x) and |f(x)| differ in that |f(x)|
_________________________________________________________
_________________________________________________________
15. Graph the functions y = √x and y = √|x|, using your calculator for the second only.
16. Complete this conclusion: The graph of f(|x|) fundamentally changes the graph of f(x) by
_________________________________________________________
_________________________________________________________
SELECTED SOLUTIONS TO HANDS-ON ACTIVITY 2.1
NOTE! You may not have worded all of your answers exactly the same, but that does not mean they are wrong. Check to see if the conceptsare correct.
2. The graph is moved down one and up two, respectively.
3. ...move up if a is positive, and move down if a is negative.
5. The graph is moved right 3 and left 1, respectively.
6. ...move left if a is positive, and move right if a is negative (although this might be the opposite of what you expected).
9. ...flip upside down, or (more mathematically) reflect across the v-axis.
11. ...reflect across the y-axis.
14. ...has no negative range. Visually, any negative portion of the graph is “flipped” so it lies above the x-axis.
16. ...replacing all the values of x < 0 with a mirror image of x > 0. The graphs f(x) and f(|x|) are always y-symmetric.
EXERCISE 4
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
DO NOT USE A GRAPHING CALCULATOR FOR THESE PROBLEMS.
1. Graph the following:
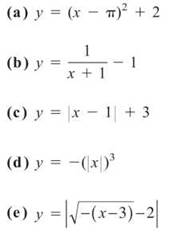
2. Explain mathematically why the graphs of y = (—x)3 and y = —(x3) are identical.
3. Given f(x) as defined in the below graph, graph the indicated translations:
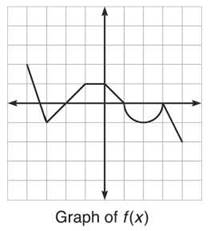
(a) f(x) – 2

(b) f(x + 1)
(c) –f(x)
(d) f(-x)
(e) |f(x)|
(f) f(|x|)

(g) g-1 if g(x) = f(x) when -3 ≤ x ≤ -1

4. Why does y = √—x have a graph if you cannot find a real square root of a negative number? (Answer based on the graph)
ANSWERS AND EXPLANATIONS
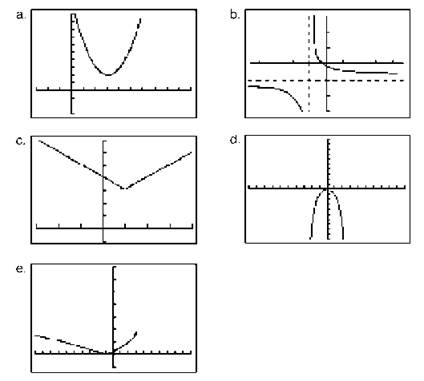
1.
2. The graphs are identical because y = x3 is odd; therefore (—x)3 = —x3.
3.
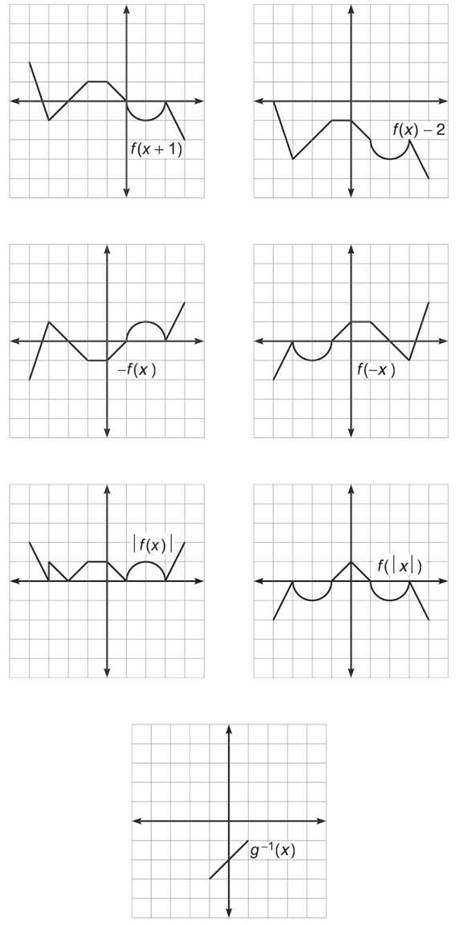
Translate each of the graphs’ defining points, as indicated in the graph. To find the inverse function in 3(g), simply reverse the order of the coordinate pair of g(x); note that g is made by the points (-3,-1), (—2,0), (—1,1) and the line segments connecting them.
4. You graphed this function in Activity 2.1, Question 10. Notice that the domain of the resulting function is (—∞,0]. A negative input will eliminate the problem of a negative radicand, as the product of two negative numbers is positive.
NOTE. Radicand is the fancy-pants term for “stuff beneath the radical sign.”