Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 10. Differential Equations
LOGISTIC GROWTH (BC TOPIC ONLY)
In addition to exponential growth, BC students need to be familiar with logistic growth. The major difference between the two is that exponential growth assumes that there are no restrictions on the quantity growing. Although billions upon billions of bacteria colonies can grow in a small area, the same is not true of, let’s say, deer. Only so many deer can be supported by a particular ecosystem; this number is called the carrying capacity for that species. After the carrying capacity has been reached, there are no longer enough natural resources to support the extended population, and it’s almost impossible for deer to get reservations in any deer restaurants (except as the main course). So, once too many deer inhabit an area, nature puts the brakes on deer- population growth.
Logistic growth looks like exponential growth at the beginning, but then changes concavity and levels out towards the carrying capacity (the upper limit for growth).
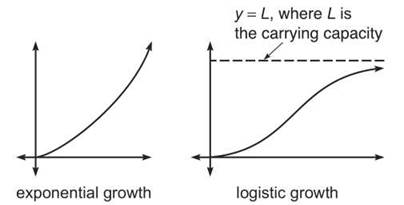
In exponential growth, the rate of change of the quantity is proportional to the quantity itself. In logistic growth, this is also true, but the quantity is also proportional to its distance from the upper bound. This translates into the formula
![]()
where L is the carrying capacity (upper bound) and k is the constant of proportionality. If you solve this differential equation using a very tricky separation of variables, you get the general solution:
![]()
It’s not worth actually solving, but both of the formulas above need to be memorized.
Example 5: A highly contagious “pinkeye” (scientific name: Conjunctivitus itchlikecrazius) is ravaging the local elementary school. The population of the school is 900 (including students and staff), and the rate of infection is proportional both to the number infected and the number of students whose eyes are pus-free. If seventy-five people were infected on December 15 and 250 have contracted pinkeye by December 20, how many people will have gotten the gift of crusty eyes by Christmas Day?
Solution: Because of the proportionality statements in the problem, logistic growth is the approach we should take. The upper limit for the disease will he L = 900; it is impossible for more than 900 people to be infected since the school only contains 900 people. This gives us the equation
![]()
We will interpret t = 0 as December 15, since that is the earliest information given. Therefore, we know that y(0) = 75. Plug that information into the equation.
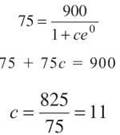
Five days later, 250 people have contracted pinkeye, so plug that information (and the c we just found) to find k:
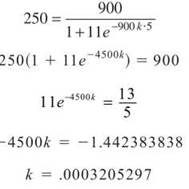
Finally, we have the equation ![]() We want to find the number of infections on December 25, so t = 10.
We want to find the number of infections on December 25, so t = 10.
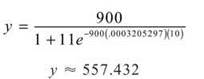
So, almost 558 students have contracted pinkeye in time to open presents.
Logistic growth can model a lot of real-world behavior; in fact, some retailers have harnessed a key feature of logistic growth. Every year, there seems to be a new toy on the market that everyone wants (Tickle Me Elmo, Furby, Cabbage Patch Kid), and fad toys like these follow a logistic sales pattern. Some stores compute the logistic growth curve (just as we did in Example 4) and stop purchasing the fad toys when the concavity of the curve changes (which means that the sales are still increasing but now at a decreasing rate). This practice helps cut down on piles of unsold product and thus decreases unnecessary spending by the store.
EXERCISE 5
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE A GRAPHING CALCULATOR FOR THESE PROBLEMS.
1. The big toy for the holiday season this year is the Tickle Me Ben Stein Doll. When you gently squeeze his tummy, Ben will giggle and talk to you about his work in the Nixon administration. The kids love it! Research shows that the rate of sales is proportional to the number sold and the number in the target audience who haven’t yet purchased it. Assume that the target audience number is 4 million. If 950,000 have been sold by 12 a.m. on October 1, and 3.5 million have been sold by 12 a.m. on December 1, on what day did the company sell to exactly half of its target audience?
2. The carrying capacity for deer in a particular small town is 2,200, and the rate of increase in their numbers is proportional to both the number, n, of deer and 2,200 — n. If there were 1,000 deer one month ago and 1,150 deer now, how many months will it take the deer to number 2,100?
3. Assume that the rate of fans being seated in Oriole Park at Camden Yards (home to the Baltimore Orioles) is proportional both to the number of fans already seated and the number of empty seats; the park has a capacity of 48,262 fans. One hour before game time, only 10 percent of the seats are filled. At game time, 85 percent of the seats are filled. Assuming that no one leaves early, what percentage of the seats are filled 2 hours into the game?
4. For what value of y is dy/dt increasing the fastest in a logistic growth curve? Justify your answer mathematically.
ANSWERS AND EXPLANATIONS
1. In this problem, L = 4,000,000. The first objective is to find c using the fact that y(0) = 950,000. (For our purposes, t = 0 is October 1.)
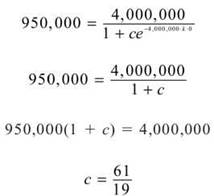
If t = 0 equates to the beginning of October 1, then t = 1 is October 2, t = 30 is October 31, and t = 61 is December 1. We know that y(61) = 3,500,000.
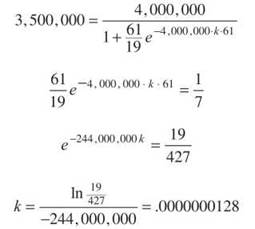
Now that we have c and k, we want to find t when y = 2,000,000 (half of the target audience).

Therefore, the sales figure was reached after t = 22 but before t = 23; this translates to October 23.
2. L = 2,200; y(0) will translate to a month ago and y(0) = 1,000; y(1) = 1,150. Use all of this information the same way you did in number 1 to find c and k. First, find c.
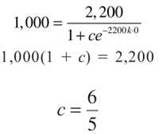
Now find k.
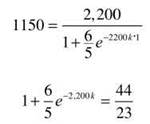
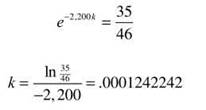
Our final goal in this problem is to calculate t when y = 2,100.

Since t = 1 translates to this month, t = 11.807 translates to 10.807 months from now.
3. L = 48,262; v(0) is one hour before game time, and y(0) = .10L = 4,826.2; y(1) = .85L = 41,022.7. Begin by finding c.
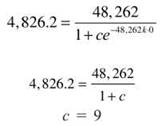
Now find k using y(1).

The problem asks us to find y when t = 3.

Two hours into the game, ![]() percent of the seats are filled.
percent of the seats are filled.
4. In this problem, you are trying to maximize dy/dt. Treat this like any optimization problem—start by finding its derivative and setting it equal to 0. (Remember, the derivative of dy/dt is written d2y/dt2.) You’ll have to use the Product Rule. Because a logistic relationship is evident, we use its general form.
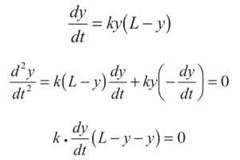
Since dy/dt is not zero, we can divide both sides by ![]() and say that
and say that
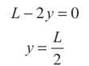
Therefore, the rate of change is the greatest halfway to the upper boundary for the logistic growth. This makes sense geometrically, because the slope of the tangent lines will increase to that point and then become less steep afterward.