Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 11. Sequences and Series (BC Topics Only)
POWER SERIES
Thus far, you have dealt exclusively with series of the form ∑an; all the series have been runs of constants. The final two sections of this chapter deal with series that contain variables, and the AP test has more questions on these topics than all the other sequences and series topics combined. Power series, the first of the essential topics, are series of the form 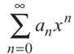 or
or 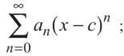 the first is said to be centered about x = 0, while the second form is centered about x = c. Strangely enough, most of our information concerning power series does not come from mathematicians, but rather from Shirley MacLaine, famous new-age celebrity. In her most recent book Out on a Leash, she claims that, among her many reincarnations, three of them were spent as power series. “It wasn’t an exciting life,”she says in the book, “but I always felt centered swimming in the c.”
the first is said to be centered about x = 0, while the second form is centered about x = c. Strangely enough, most of our information concerning power series does not come from mathematicians, but rather from Shirley MacLaine, famous new-age celebrity. In her most recent book Out on a Leash, she claims that, among her many reincarnations, three of them were spent as power series. “It wasn’t an exciting life,”she says in the book, “but I always felt centered swimming in the c.”
Your major goal with power series will be (surprise, surprise) to determine where they converge. Notice that we are not trying to determine if they converge, but rather where they converge. All power series will converge at the x-value at which they are centered (x = c). To test this, plug x = c into the generic power series centered at c:
![]()
Will power series converge at other points? Possibly. One of three things will happen:
(1) The power series will only converge when x = c.
(2) The power series will converge at c and some distance around c (called the radius of convergence, or ROC). For example, if a series centered about 3 (c = 3) has a radius of convergence of 4, then the series will converge when x is between — 1 and 7.
NOTE. Power series usually start with n = 0, rather than n = 1.
(3) The power series will converge for all x (in this case, the radius of convergence is ∞).
To find the ROC for a power series, you’ll use the Ratio Test, since power series by definition contain powers of n, which grow large quickly as n increases. In fact, you will always test for absolute convergence when finding the ROC to simplify matters. Once you find the ROC, you will sometimes be asked whether or not the series converges at the endpoints of that interval. For example, our series centered about 3 with ROC = 4 have an interval of convergence (IOC) of [—1,7),(—1,7],[—1,7], or (—1,7), depending upon which endpoints cause the series to converge.
NOTE. If the series converges only at x = c, the radius of convergence is 0.
Example 12: Find the radius of convergence for the following power series:
(a) 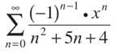
Use the Ratio Test to see if the series converges absolutely:

As n approaches infinity, 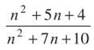 approaches 1.
approaches 1.
![]()
Remember, the Ratio Test only guarantees convergence if that limit is less than one. Since the limit is x, the series will only converge if |x| < 1 or —1 < x < 1. The series is centered at c = 0 and has ROC = 1.
NOTE. The series may or may not converge at the endpoints x = -1 and x = 7. You’ll have to test those points separately in the series.
(b) 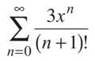
This is another power series centered at c = 0. To see where it converges, use the Ratio Test to see if the series converges absolutely:
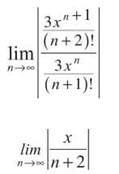
Remember that x is some number you’ll plug in later, so even though it’s technically a variable, you can treat it like a number. Whatever number it is, it’s irrelevant in this problem. The denominator will grow infinitely large, so
![]()
The Ratio Test only guarantees convergence when the limit is less than 1. In this case, the limit is 0, which is always less than 1, regardless of what x is. Therefore, this series converges for all x, and the radius of convergence is ∞.
Example 13: On what interval does the series ![]() converge?
converge?
Solution: For a change, this power series is centered at c = —2, since (x — (—2)) = (x — c). This question asks for the IOC; we still need to find the ROC first:
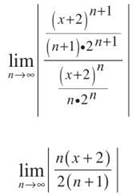
As n approaches infinity, ![]() approaches 1/2, so the limit is
approaches 1/2, so the limit is ![]() Remember that this must be less than 1 in order for the series to converge:
Remember that this must be less than 1 in order for the series to converge:
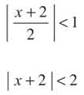
The radius of convergence is 2. The series is centered at x = —2, so the series converges on (—2 — 2, —2 + 2) = (—4,0).
We’re not done yet! We need to see if the series converges at the endpoints of the interval, x = —4 and x = 0. Let’s plug each separately into the original series to see what happens.
x = —4:
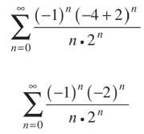
TIP. Once you simplify the Ratio Test to get │x — c│ < d, the d represents the radius of convergence. In Example 13, you simplify to get │x + 2│ < 2; here, c = 2, so that is the radius of convergence.
Regardless of what n is, the numerator will be positive in this series. In essence, you will have the series
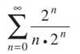
If you cancel out the 2n, you have
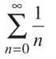
which is the divergent harmonic series. Therefore, the series does not converge for x = —4.
x = 0:
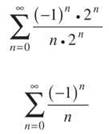
This is the alternating harmonic series that satisfies all the conditions of the Alternating Series Test and thus converges. Therefore, the series does converge when x = 0.
The IOC for 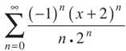 is (—4,0].
is (—4,0].
Because power series contain x’s, they can also be used to define functions:
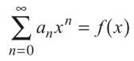
As long as the series converges on the interval (c,d), it will return a sum for any value between c and d, that sum will be the function value for the given input. Functions defined as power series have two important characteristics:
(1) Derivatives or integrals of functions defined by power series have the sum e radius of convergence as the original function. However, the endpoints may act differently, so you’ll have to check them again. Thus, although the radius of convergence will be equal, the interval of convergence may not be.
(2) To find the derivative or integral of a function defined by a power series, simply differentiate or integrate the given power series just as you have done previously. All of the techniques you have used to find derivatives and integrals of regular functions still apply for power series functions.
Example 14: If ![]() find the interval of convergence for f(x) and ∫f(x)dx.
find the interval of convergence for f(x) and ∫f(x)dx.
Solution: This power series (centered at x = 0) is actually just a geometric series with a = 1 and r = 3x/4. Geometric series only converge when │r│ < 1:
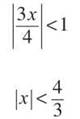
The radius of convergence for this series is 4/3, so the series converges on (—4/3,4/3). To find the interval of convergence, plug in the endpoints:
x = —4/3:
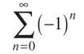
This is a divergent alternating series.
x = 4/3:
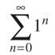
This diverges by the nth Term Divergence Test.
Therefore, the IOC for ![]() The next part of the question asks you to find the IOC for ∫f(x)dx, so begin by integrating the series with u-substitution:
The next part of the question asks you to find the IOC for ∫f(x)dx, so begin by integrating the series with u-substitution:
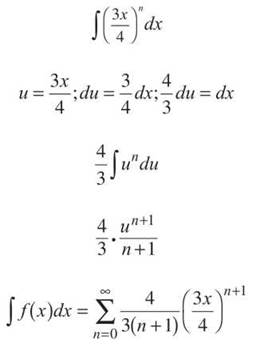
The integral will have the same ROC, but we need to recheck the endpoints to see if the IOC changes:
x = —4/3.
![]()
This is a convergent alternating series.
x = —4/3.
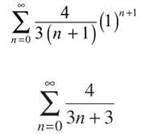
You can compare this with the series 1/n and apply the Limit Comparison Test:
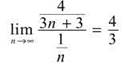
Therefore, both series diverge.
The interval of convergence for ![]()
EXERCISE 3
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
DO NOT USE A GRAPHING CALCULATOR FOR THESE PROBLEMS.
1. Find the radius of convergence for each of the following:
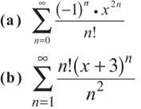
2. The series 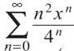 converges on what interval?
converges on what interval?
3. If ![]() give the interval of convergence for f'(x).
give the interval of convergence for f'(x).
ANSWERS AND EXPLANATIONS
1. (a) Apply the Ratio Test to see if the series converges absolutely:
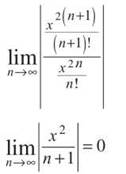
Remember, the n approaches infinity while the x stays the same; therefore, the limit is 0, regardless of x. Because 0 < 1 (still), this series converges for all x, and the radius of convergence is ∞. The interval of convergence is (—∞,∞), if you’re curious.
(b) Apply the Ratio Test. Once you simplify the complex fraction, you get
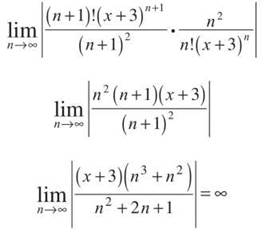
Because the degree of n in the numerator is higher, this rational expression will become infinitely large. Therefore, this limit is never less than 1 and can never converge, according to the Ratio Test. Remember that all power series converge—at least for the x value at which they are centered. Therefore, the series converges only for x = —3, and the radius of convergence is 0.
2. Begin by finding the radius of convergence:
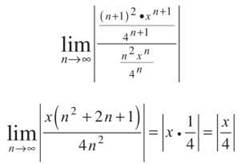
According to the Ratio Test, the series converges if
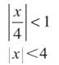
So, the radius of convergence is 4 for this series centered at 0. The series must converge on (0 — 4, 0 + 4) = (—4, 4). Now you have to see whether or not the series converges at the endpoints by plugging them in for x:
x = —4:
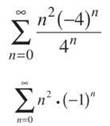
This diverges by the nth Term Divergence Test,
x = 4:
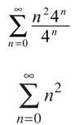
This diverges by the nth Term Divergence Test, too, and both endpoints have failed us.
Therefore, the series ![]() converges on (—4, 4).
converges on (—4, 4).
3. The function and its derivative will both have the same radius of convergence, so you can find the ROC of the original function first.
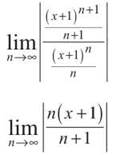
As n approaches infinity, ![]() approaches 1.
approaches 1.
![]()
According to the Ratio Test, the series converges if |x + 1| < 1, so the radius of convergence (as always) is that number on the right side once we’ve solved for |x — c|; in this case, the ROC is 1. Since the power series is centered at c = —1, we know (so far) that the series converges on the interval (—1 — 1, —1 + 1) = (—2, 0). Now, it’s time to take the derivative of the series and test the endpoints x = —2 and x = 0. Use the Power Rule to take the derivative:
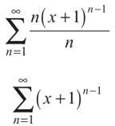
Both endpoints make the series diverge by the nth Term Divergence Test if you plug them in, so the interval of convergence is (—2, 0).