Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 11. Sequences and Series (BC Topics Only)

TECHNOLOGY: VIEWING AND CALCULATING SEQUENCES AND SERIES WITH A GRAPHING CALCULATOR

Your calculator can serve three major functions to assist you in this chapter: it can graph sequences, graph series, and calculate partial sums. Be warned ahead of time: The calculator commands to accomplish these tasks are not as friendly as the commands used to evaluate a definite integral. It may take a bit of practice before these techniques become second nature.

In the first problem set, way back in the beginning of this chapter, you had to determine whether or not the series 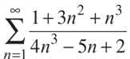converged. Hopefully, this problem is much easier now; the series clearly diverges because of the nth Term Divergence Test, since

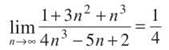
In order to show that the sequence approaches 1/4 as n approaches infinity, you’ll have to change the [Mode] to “seq”uence. This changes the [Y=] screen to the “u(n)” screen; type the sequence in for u(n). (The [x,t,θ,n] button will now display an “n.”)

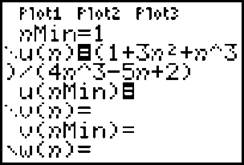
NOTE. The [Window] settings for my graph are nMin = 1, nMax = 50, PlotStart = 1, PlotStep = 1, Xmin = 0, Xmax = 50, Xscl = 5, Ymin = .1, Ymax = .5, and Yscl = 1.

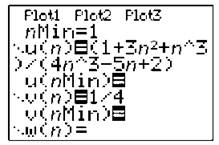
If you choose friendly [Window] settings and press [Graph], the sequence clearly levels off. If you enter a second sequence of 1/4 for v(n), it’s easier to see that the sequence does indeed begin to level off at 1/4.

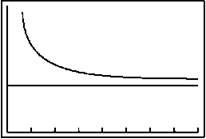
Remember that although the sequence converges to 1/4, the series will diverge by the nth Term Divergence Test. In order to visualize this, we can graph that series. To do so, however, you’ll need to make some minor setting changes on your calculator. First of all, go to the [Mode] screen and select “Par”ametric mode and “Dot” rather than connected. Now, go to the [Y=] screen and set X_IT = T. The Y_IT is the tricky part:

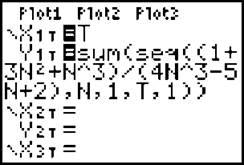
NOTE. My [Window] settings for this graph are Tmin = 1, Tmax = 35, Tstep = 1, Xmin = 0, Xmax = 35, Xscl = 5, Ymin = 5, Ymax = 15, and Yscl = 1.

To get the “sum” command, you need to press [2^nd] → [Stat] → “Math” → “sum”, (and the “seq” command comes from [2^nd] → [Stat] → “Ops” → “seq”. (The “N” used is the letter N, which is the result of pressing [Alpha] → [Log]. The syntax for a sequence is seq (sequence of n ,n,whatever n= in sigma, T,I).

Choose nice [Window] settings for the graph (it might take a couple of tries to pick good settings), and you get a good picture of the series:

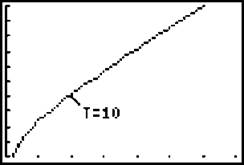
This series is definitely divergent—it approaches no limiting height. Furthermore, at approximately n = 10 (on the graph t = 10), the terms progress almost in a linear fashion. Can you guess what the slope of that line is? Ill spare you the suspense: it’s 1/4, since the sequence tells us we will be adding approximately 1/4 to each term forever. If you aren’t all that impressed with the series-graphing capability of the calculator (we really did have to force it, didn’t we?), then you’ll probably be equally unimpressed with the calculator’s ability to calculate partial sums. The process is very similar to the series graph. Although the series 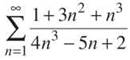diverges, you can still find the sum of its first n terms. Let’s use the calculator to find S₂₀₀. You do not have to use the [Y=] screen, as this is simply a command you can type out on the regular screen:

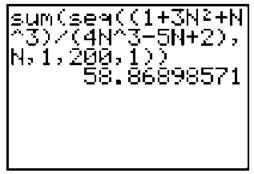
Therefore, S₂₀₀ ≈ 58.869. You can easily tell that this series diverges if you calculate S₃₀₀ ≈ 84.173. Clearly, the series is not “leveling out” and approaching a limiting value even when the n is this large. However, the calculator does have its limitations. If you type too large a value for n, you will get an error message. Texas Instruments technicians explain that this occurs because the calculator is “tired of adding so many dang numbers, for Pete’s sake ... let it do something interesting for a change.”

EXERCISE 5

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

YOU MAY USE A GRAPHING CALCULATOR FOR PROBLEMS 6 AND 7 ONLY.

1. Determine whether or not the series 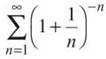converges, and justify your answer.

2. Find the interval of convergence for the power series:

3. If P(x) = 2 + 3(x + 1) — 6(x + 1)² is a Taylor polynomial for f(x), write a third-degree Taylor polynomial for

4. Does the series converge absolutely, converge conditionally, or diverge?

5. Find the value of a so that the radius of convergence for the series 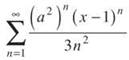is 1/4 and a > 0.

6. If g(x) = e^sin x, use a fourth-degree Maclaurin polynomial to approximate g'(.3).

7. Find the sum of each of the following series. If you cannot find the exact sum, find it accurate to four decimal places:

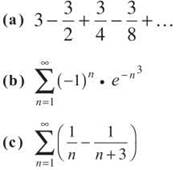
8. James’ Diabolical Challenge: Prove the convergence or divergence of the series 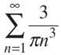using four different convergence tests.

ANSWERS AND EXPLANATIONS

1. The nth term of the series is as n approaches infinity, you get 1/e, which is not 0. Therefore, this series fails the nth Term Divergence Test and therefore diverges.

2. This is the series 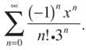To find the interval of convergence, use the Ratio Test to see where the series converges absolutely:

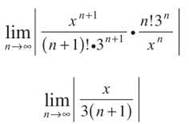
Regardless of x, this limit will be 0 as the denominator will grow infinitely large. Therefore, this limit is always less than 1, so this series always converges. The interval of convergence will be (—∞,∞). No need to test endpoints, since an interval can’t be closed at an unbounded (infinite) endpoint.

3. To find m(x), integrate:

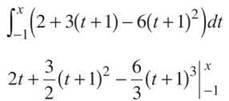
Apply Fundamental Theorem Part One:

All of the polynomial terms will cancel out when you plug in x = —1, except for 2(—1). You can write your final answer by simplifying:

or by factoring out a 2.

Either of those answers is acceptable.

4. First, ignore the fact that it is an alternating series to see if the convergence is absolute. The Ratio Test serves the best to test for convergence because of the factorial.

As n approaches infinity, this value will grow extremely small. Each of the binomials in the denominator will be huge, and their product will be even larger. 1 divided by a high number is 0. Since 0 < 1, this series converges absolutely. Remember, this means that the original alternating series converges automatically.

5. Find the radius of convergence as usual, using the Ratio Test:

As n approaches infinity, the limit of is 1, making the overall limit

This limit must be less than 1 to make the series converge.

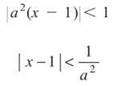
We also know that the radius of convergence is 1/4; we had a shortcut that said whenever we solve for │x — c│, the number on the other side of the inequality is the radius of convergence. Thus,

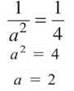
a cannot equal —2, since the problem specified that a > 0.

6. We already know the Maclaurin series for e^x, so plug sin x in for x to get the Maclaurin polynomial for e^{sin x}:

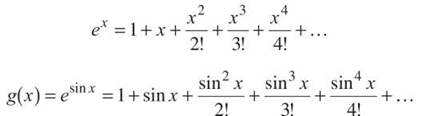
If you read the question carefully, you see that it asks you to find an approximation for g'(x), the derivative of the series above. However, the series above has one too few terms written. Since the equation above is of degree 4, its derivative will have degree 3, so add another term when you take the derivative.

Use this ugly monster to approximate g'(.3) by plugging .3 in for x. The resulting approximation is 1.2837864. The actual value for g'(x) = (cos x)(e^{sin x}) = 1.2838053.

7. (a) This is the geometric series The infinite sum is given by

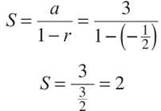
(b) This is a convergent alternating series, according to the Alternating Series Test. However, you cannot usually find the sum of such a series (with the exception of part (a) above). Instead, remember that the remainder (or error bound) in an alternating series is the absolute value of the first omitted term. Therefore, we should calculate the values of a few terms in the alternating series until one of the term’s values ensures accuracy to four decimal places.

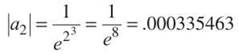
The term a₂ is the remainder for S₁, the sum of the n = 1 term. The above means that S₁ is accurate to three decimal places, but the fourth decimal place could be off by as much as 3, so try a₃:

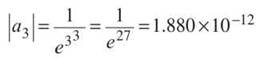
This one definitely cinches it. The sum S₂ will be accurate to 11 decimal places. All that remains is to find S₂:

If you are dubious, use your calculator to find S₅₀₀, and you’ll find that we were quite accurate, even after only two terms.

(c) This is a telescoping series, and you can find the exact sum by expanding the series to determine which terms will cancel out as n approaches infinity:

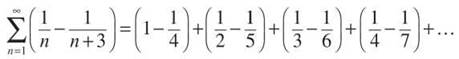
Every number from 1/4 lower will be canceled out by its opposite as the sum gets longer and longer. Therefore, the exact sum is composed of the only numbers that do not get canceled:

8. Okay, so four tests is a little overkill; although it’s true that only one is necessary, this problem wouldn’t be diabolical otherwise, would it?

P-series Test: If you factor the 3/π out of the series, you get 1/n³ is a p-series with p = 3, so the series converges. The fact that you multiply the sum by 3/π when you’re finished does not change the fact that the sum is a finite number.

Integral Test: The series will converge if

exists.

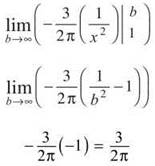
Because the limit is a finite number, both the integral and the series converge.

Limit Comparison Test: Compare the series to 1/n³.

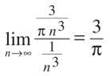
Because the limit is a finite number, and 1/n³ is a convergent p-series, then both series must converge.

Comparison Test: Each term in the series is less than the corresponding term in the series You know this because 3/π < 1. When you multiply 1/n³ by a value less than one, the result is smaller than 1/n³. Notice that 1/n³ is a convergent p-series. Because the terms of are less than a convergent series, it must also converge by the Comparison Test.

SUMMING IT UP

• A sequence is basically a list of numbers based on some defining rule.

• The Comparison Test is also called the Direct Comparison Test.

• The trickiest part of the Comparison Test is deciding what to compare the given series to. Most of the time, you pick a series that is close to, but simpler than, the given series.

• When choosing the Comparison Series, use only the highest powers of n in the numerator and denominator of the original series.