Master AP Calculus AB & BC

Part III. FOUR PRACTICE TESTS

ANSWER KEY AND EXPLANATIONS

Section I, Part A

1. The correct answer is (D). Solve this integral using u-substitution. Let u = 2x, so du = 2dx.

becomes which yields

2. The correct answer is (B). This is a rather complicated Chain Rule application. The derivative of tan u is sec²u du, but we mustn’t forget to also take the derivative of e^sinx. Since

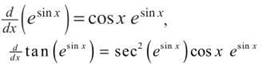
3. The correct answer is (E). Be careful here. Although it resembles a Fundamental Theorem Part Two problem, it is not. The problem asks for F(2), not F'(2)! So,

4. The correct answer is (C). Straight-forward evaluation of a derivative at a point problem: f'(x) = 2tanxsec²x + cosx. So,

5. The correct answer is (A), We need both the first and second derivatives to be negative for this function to be decreasing and concave down. f’(x) = 4x³ — 6x² — 4x and f"(x) = 12x² — 12x — 4. By using the wiggle graph below,

we can easily see that choices (B) and (C) can be eliminated, so we must check out the values of f"(—2), f"(—1), and f"(1). f"(1) = —4 < 0.

6. The correct answer is (E), Here, we should take the derivative of each I, II, and III and see what we get.

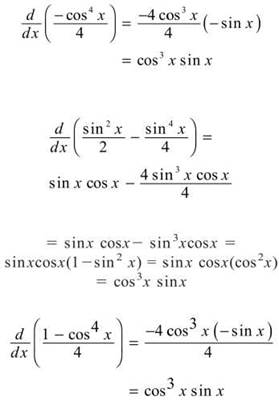
7. The correct answer is (D), Another lengthy Chain Rule—just don’t forget to take the derivative of 2x, the argument of the argument. Since the derivative of e^u is e^u du and the derivative of sinu is cosu du, then

8. The correct answer is (D). Remember, speed is the absolute value of velocity. Since |—15│ > |10|, the maximum speed is reached at t = 5 seconds.

9. The correct answer is (E), Acceleration can be thought of as the absolute value or slope of velocity. The slope of the velocity curve is steepest on [5,6].

10. The correct answer is (B), In order to write the equation for a line, we need its slope and a point on that line. We already have the point, (π/2,1), so the big problem is determining its slope, which is the derivative of the curve when x = π/2 ∙ y' = cosx — 2sinx, so y’(π/2) = —2. Using point ≠ slope form, the equation for the line could be written as Since this is not a choice, we must change this to standard form, 2x + y = π + 1.

11. The correct answer is (B), Since the f is decreasing over (—∞,—1), its derivative, f', must be negative over this same interval. This eliminates choices (C), (D), and (E). Examining the interval (—1,0), the graph of f is decreasing here; thus, the graph of f' must be negative. Only choice (B) meets this requirement.

12. The correct answer is (D), By examining the second-derivative wiggle graph below, we can see that the second derivative is positive at, before, and after 2. Therefore, there is no point of inflection at x = 2.

13. The correct answer is (C). Pretty simple problem—we determine the derivative, set it equal to zero, and use a wiggle graph.

Since 3e^sinx will never be 0, we set cosx = 0 and solve.

cosx = 0 when for any integer n. By examining the wiggle graph below, we can see that the derivative is negative over

14. The correct answer is (D). This one seems tricky, but it actually works out quite quickly. If h(x) = f(g'(x)), then by using the chain rule, h'(x) = f'(g'(x))g"(x). The problem tells us that f'(x) will always be positive. Since h’(3) somehow becomes negative, g"(3) must be negative. Therefore, g must be concave down at x = 3.

15. The correct answer is (D). Do we understand the definitions of continuity and differentiability?

(A) Does the limit exist as x approaches 3? Yes.

(B) Is f continuous at x = 5? Yes.

(C) Does f'(2) = 0? Yes. (It has a horizontal tangent line.)

(D) Does f'(4) exist? No.

(E) Is f(2.5) > f'(2.5)? Yes. (f(2.5) > 0, and since f is decreasing at x = 2.5, f'(2.5) < 0.)

16. The correct answer is (E). We should always sketch the region.

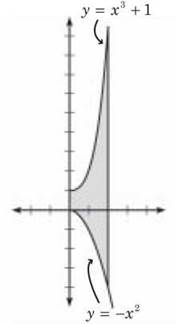
As we can see, y = x³ + 1 is above y = —x² over the entire interval. So,

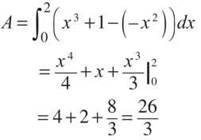
17. The correct answer is (C). Some implicit differentiation: Remember, everything here is differentiated with respect to x. Don’t forget the product rule for 3xy.

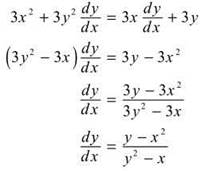
18. The correct answer is (D). This is a very simple u-substitution integral. Let u = 2x, so du = 2dx. It follows that becomes

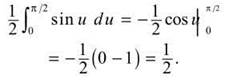
19. The correct answer is (D). Again, we will rely on the magic of the wiggle graph to supply us with the solution to this differentiation problem.

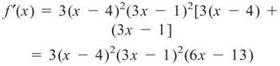
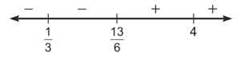
By setting f'(x) = 0 and solving, we quickly discover that the zeros of the derivative are 1/3, 13/6, and 4. By examining the wiggle graph below, we can see that the only value where the derivative changes from negative to positive is at x = 13/6.

20. The correct answer is (C). Whenever the problem asks for the “average value of the function,” we should immediately think of the mean value theorem for integration. We are looking for f(c) in this formula: Applying the MVT for Integration here yields the following equation:

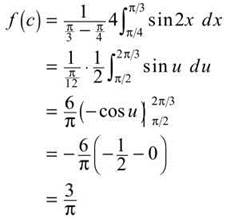
21. The correct answer is (B). Remember, limits at infinity are like horizontal asymptotes. If the top degree is greater than the bottom degree, the limit does not exist. If the bottom degree is greater than the top degree, the limit is zero. If, as in this case, the degrees are equal, then the limit is the ratio of the leading coefficient of the numerator over that of the denominator. Here, that ratio is —5/11.

22. The correct answer is (C). Sketch the curve. We may simplify the expression first by using cancellation. However, we must remember that by canceling out a term involving x, we are removing a discontinuity. So, the graph of the original function will have a point discontinuity.

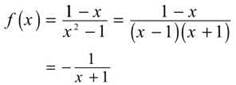
with a point discontinuity at x = 1.

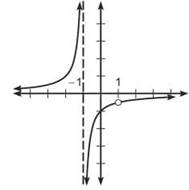
By examining the graph above, we can see that it is concave down to the right of the asymptote. These are actually two intervals, because the function is not continuous at x = 1. They are (—1,1) and (1,∞).

23. The correct answer is (C). The two curves, y = √x and y = x² intersect at x = 0 and x = 1. So, these will be our limits of integration. For x values between 0 and 1, √x > x². This being the case, when we determine the area of the region, we should subtract √x - x². Therefore,

24. The correct answer is (D). This is just the derivative of f(x) = tan2x evaluated at x = π/8. f’(x) = 2sec²2x, so

25. The correct answer is (E). A little tricky u-substitution integral. Let u = ln x, then du = dx/x. It follows that

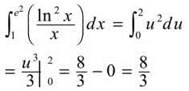
26. The correct answer is (D). Since the question asks for average velocity and we are given the position equation, we should determine the slope of the secant line:

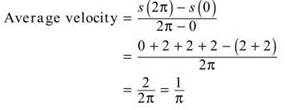
27. The correct answer is (C). Since then exists and is equal to 2 as well.

28. The correct answer is (E). This is a rather challenging related-rates problem. We are looking for dA/dt when h = 24. First, we need a primary equation. This will be the formula for the area of a triangle:

Since the base is a constant, 10, this becomes

Differentiating with respect to t yields

How do we determine dh/dt? We must find a relationship other than involving h. How about using the tangent equation?

Differentiating this with respect to t yields

Since we know this equation becomes

The last unknown to identify is 10sec²θ. We can use the Pythagorean theorem to help here. Since h = 24 and b = 10, the hypotenuse must be 26. So,

Plugging this expression in for dh/dt gives us

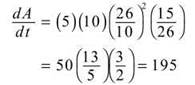
Section I, Part B

29. The correct answer is (A). We must use the quotient rule to evaluate the following derivative:

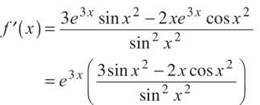
30. The correct answer is (E). To write the equation for a line, we need the slope of the line and a point on the line. We already have its slope, since f'(x) = 10; the slope of the tangent line is 10 as well. To find the point on the line, we must set the derivative of f equal to 10 and solve for x; then, substitute this x-value into t to determine the corresponding y-value.

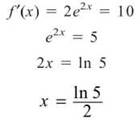
Now, we substitute this value into f and the result is

Our problem has now been reduced to determining the equation for a line that passes through (ln5/2,5) and has slope 10. Point-slope form of this equation is

Converting to slope-intercept form and using the calculator to evaluate the value of ln5/2, we get

y = 10x — 3.047

31. The correct answer is (D). This is an area accumulation problem. The function decreases from x = 0 to x = 1 by an amount equivalent to the area between the graph off and the x-axis, which is —2 units squared. This was determined by finding the area of the triangle. The function then increases from x = 1 to x = 2 by 3/2 units squared. From x = 2 to x = 4, it increases 3 + 3/2 or 9/2 units squared. From x = 4 to x = 6, the function decreases 2 units squared. Putting all of this together, we can see that the function’s value is greatest at x = 4, followed by at x = 6, then at x = 0, and least at x = 2.

32. The correct answer is (E). This is the limit of the difference quotient that is the definition of the derivative. All this means is that f'(5) = 3. For I., does the function’s value necessarily equal the derivative’s value? No, so I. is out. Since the derivative exists at x = 5, the function is differentiable there. Remember that differentiability implies continuity, so the function must be continuous at x = 5 as well.

33. The correct answer is (C). Use the calculator to graph the derivative given. Where the graph changes from positive to negative will be the local maximum. This occurs at x = 0.511.

34. The correct answer is (B). Related rates—oh boy! First, let’s draw the following diagram:

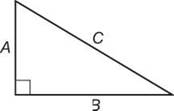
We are looking for dC/dt. We know that dA/dt = -40 and dB/dt = -30. Now, we need an equation to relate A, B, and C. Since this is a right triangle, we can certainly use the Pythagorean theorem:

A² + B² = C²

Differentiating with respect to t, which we do in every related-rates problem, yields

Solving this equation for dC/dt gives us

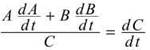
What are the values of A, B, and C? To answer this, we use the facts that the cars each started 100 miles from Millville and have been traveling for 90 minutes or 3/2 hours. Car A has traveled 60 miles, so A = 40. Car B has traveled 45 miles, so B = 55. By the Pythagorean theorem, Substituting these values into the equation yields

35. The correct answer is (D). This problem is best answered using the graphing calculator. If we examine the graph, we can see that it is continuous at x = —1. The graph has a jump discontinuity at x = 1; it is not differentiable there. Since the graph is increasing before and decreasing after x = —1, there is a local maximum at x = —1.

36. The correct answer is (A). This is an optimization problem. Let’s first express the product x²y only as a function of x:

Next, we differentiate and set the derivative equal to zero and solve for x to determine our critical values:

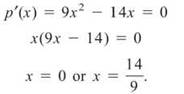
By examining the wiggle graph below, we can see that the function’s minimum occurs at x = 14/9.

The problem asks for the minimum product. So, we must substitute 14/9 back into p(x), and we get —5.646.

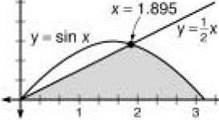
37. The correct answer is (C). Use your calculator to determine where these two curves intersect. This intersection point will give us a limit of integration. Since the graph of y = sin x is above the graph of y = 1/4x — 1, we integrate to find the area:

Our calculator will then do all the work and give us

A = 3.926

38. The correct answer is (E). Be careful here—make sure you have the right region, as shown in the diagram below:

The best method to use, since we are rotating about the y-axis, would be shells. However, we will need to break it up into two regions.

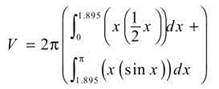
Using our calculator,

V = 17.117

39. The correct answer is (E). Set the derivative off equal to —1.024, and solve. By the quotient rule, we have

Graphing and determining the intercept yields x = 4.797.

40. The correct answer is (C). Since g is an antiderivative of f, then f is the derivative of g. The graph of the derivative of g changes from negative to positive at x = c, so g has a minimum there.

41. The correct answer is (B). Use your calculator for this one. First, determine the second derivative of f. Graph it, and find the x-intercept.

Our calculator shows us that the x-intercept of this second derivative is 0.4985.

42. The correct answer is (C). We have the graph of the derivative, but we are looking for the graph of the function. Since the derivative’s graph is continuous, there are no discontinuities, cusps, or vertical tangents on the function’s graph. This eliminates choices (A), (D), and (E). Since the derivative is positive and increasing from x = 0 to x = a, the function must be increasing and concave up over this same interval. Between the two choices remaining, only (C) meets this requirement.

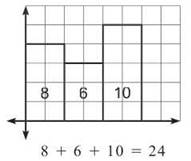
43. The correct answer is (D). This problem requires a little drawing. We should plot the seven points, draw the rectangles, find the area of each one, and add them up.

44. The correct answer is (E). Let’s examine each statement: Since there is an obvious cusp at x = a, (A) is a true statement. (B) says that the left-hand derivative does not equal the right-hand derivative at x = a, which means that there must be a cusp there—which there is. So, this is true also. The hole at x = c would indicate that f(c) is undefined, so (C) is true. (D) is true because there is a horizontal tangent at x = b. Since the discontinuity at x = c is removable, the exists, is false.

45. The correct answer is (D). In this problem, the question is for what value of k will the area under equal Setting these two integrals equal to each other and solving for x yields

To determine the correct value of C, the constant of integration, we should use the condition given to us, p(0) = 5:

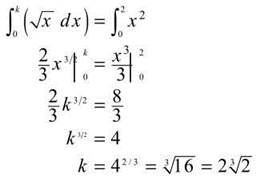
Section II, Part A

1. (a) At t = 5, v(t) = 1.1904 > 0, which indicates that the velocity is positive. Therefore, the particle is moving to the right.

(b) Since the velocity function is given, this is an application of the mean value theorem for integration, which says that

Average value

Applying that formula to this problem leads to

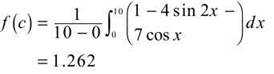
(c) Remember that acceleration is the derivative or slope of the velocity curve. So, we want the average slope of the velocity from t = 0 to t = 10. In other words, we want the slope of the secant line from t = 0 to t = 10.

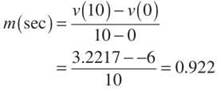
(d) Here, we need to determine the position equation, p(t). In order to determine the position equation, we should find an antiderivative of the velocity equation, v(t).

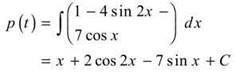
To determine the correct value of C, the constant of integration, we should use the condition given to us, p(0) = 5:

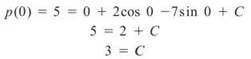
Substituting this value back into the position equation gives us p(t) = x + 2cos 2x — 7sin x + 3. Now, to answer the question: p(2) = 2 + 2cos 4 — 7sin 2 + 3 = -2.672

2. a)

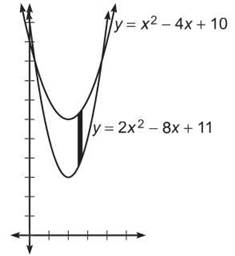
(b) We use the definite integral to determine the area of this region. We must first use the calculator to determine the points of intersection of the graphs. The x-coordinates will give us our limits of intersection.

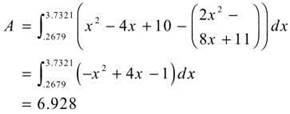
(c) To determine the volume when the region R is rotated about the y-axis, we are going to use the shell method:

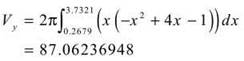
(d) Insert k for the upper limit of integration, set the volume expression equal to half of the solution for part C, and solve for k.

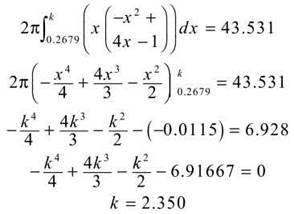
k was determined by graphing the function and determining the x-intercept.

3. (a) The equation should indicate that we are dealing with this exponential growth or decay model:

A(t) = Ne^kt

Since we are given that the initial amount of water was 100 gallons, we know that N = 100. We can determine k by substituting values for N, t, and A(t) and solving for k, as such:

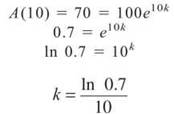
Now that we have determined both constants, N and k, we can write our expression A(t):

(b) This problem is kind of tricky. To determine the amount of water that had leaked out after 5 hours, we should find how much is still in the reservoir, which is A(5), and subtract that from the initial amount, 100 gallons.

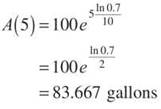
This represents the amount still in the reservoir. The amount of leakage would be 100 — 83.667 = 16.333 gallons

(c) By applying the mean value theorem for integration, we get

Average amount =

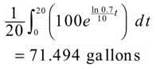
(d) We know the amount, A(t), is equal to 71.494. We set Equation (2) equal to this and solve for t.

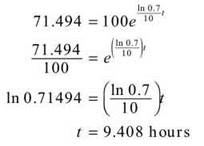
Section II, Part B

4. (a) To draw a slope field, you plug each of the indicated coordinates into dy/dx for x and y. If the resulting slope is undefined, you can indicate that with a small vertical line (since the slope of a vertical line is undefined). Your answer should look something like this

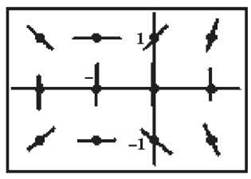
(b) The slope field’s shape suggests a hyperbola centered at (—1,0), but the question requires us to justify our answer mathematically. The easiest way to justify the answer is by actually solving the differential equation by separation. (Remember, in the following steps, C represents any constant. Therefore, multiplying a constant by any number or adding any number to a constant results in another constant. For the sake of ease, we just continue to use the same symbol for that constant—C.) Begin by cross- multiplying to separate x’s and y’s

y dy = (x + 1)dx

Now, integrate both sides of the equation and multiply by 2 to make it prettier.

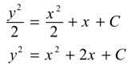
To put this into standard form for a conic, complete the square for x.

If you subtract y², you get the equation of a hyperbola. This is all the justification you need to get the question completely correct.

(c) If the hyperbola contains point (2,4), substitute these values into your answer for part (B), and you get the corresponding value for the constant C.

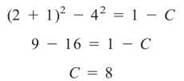
Therefore, the exact solution to that particular differential equation is

If you want to put it into standard form, you can:

5. (a) Here, we must use implicit differentiation, because x and y are not separated for us. We will differentiate both sides of the equation with respect to x, group the terms with a dy/dx, and solve for dy/dx.

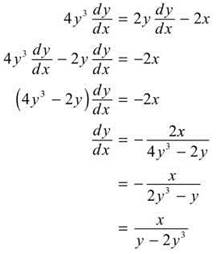
(b) In order to have a horizontal tangent, the derivative must equal zero. Let’s set dy/dx equal to zero and solve for x. Remember, in order for a rational expression like our dy/dx to equal zero, the numerator must equal zero. So, we’ll just set the numerator of our expression for dy/dx equal to zero, as such:

2x = 0, so x = 0

Now, we will determine the corresponding y-value(s):

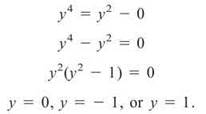
Upon closer examination, y ≠ 0 because the function does not exist when y = 0; that is, the denominator will equal zero there. So, our two points when the tangent line is horizontal are (0, — 1) and (0,1). This leads us to the equations for the horizontal tangents:

y = —1 and y = 1

(c) Remember that the slope of a vertical line is undefined. That means that we look for points where the derivative is undefined (i.e., where the denominator of the derivative is equal to zero). This time we will set the y — 2y³ equal to zero and solve for y.

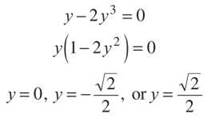
The corresponding x-values are x = 0, x = —1/2, and x = 1/2. Because vertical lines have equations of the form x = a, the x-values are all we need to write the equations for the vertical tangent lines:

x = 0, x = —1/2, and x = 1/2

(d) In order for the line and the curve to be tangent, two things must be true: They must intersect and have equal slopes. For the slopes to be equal, we should set their derivatives equal. Let’s determine dy/dx for the line:

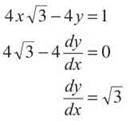
Next, we will solve the equation of the line for x in terms of y:

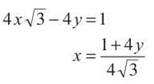
When the derivatives are equal, they are equal to √3. So, now we will set the expression for the derivative of the curve equal to √3.

We already have

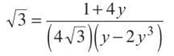
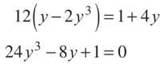
How do we solve this without our calculator? Let’s try synthetic division with 1/2. Why 1/2? Remember the rational root theorem? It told us to try factors of the constant term over factors of the leading coefficient. Since 1/2 worked in our synthetic division, 1/2 is a solution. We will now find the x-coordinate of the point of tangency by substituting this y-value:

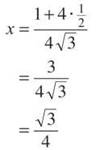
We have both our x- and y-coordinates now, so we can determine that our line and curve are tangent at

6. (a) To determine g(0), we have to find the area under the curve from x = 3 to r = 0. This is the opposite of the area under the curve from x = 0 to x = 3. Since the area of a circle of radius 3 is 9π, then the area of this quarter circle must be -9x/4. So, g(0) = -9x/4. g(8) would be the area of the triangle with base 5 and height 3. So, g(8) = 15/2.

(b) The only interval for which g is increasing is [3,8]. So, the maximum value of g is at x = 8. The maximum value of g is 15/2.

(c) We need a point and a slope. Since f(11) = —5, then g'(11) = —5. Hence, the slope of the tangent line is —5. To determine the y-coordinate of the point on the line, we must determine g(11). By area accumulation, we can see that g(11) = 0. This leads us to the following equation for the tangent line:

y = -5(x - 11)

or

y = -5x + 55

(d) Points of inflection occur only when the derivative of the derivative is equal to zero. Since the graph of f the derivative of g, does not have any horizontal tangents, then f', or g", will never be zero. Thus, g has no points of inflection.