Practice Test 3: AP Calculus BC - FOUR PRACTICE TESTS

Master AP Calculus AB & BC

Part III. FOUR PRACTICE TESTS

ANSWER SHEET PRACTICE TEST 3

Section I, Part A

Section I, Part B

Practice Test 3: AP Calculus BC

SECTION I, PART A

55 Minutes • 28 Questions

A CALCULATOR MAY /VO 7 BE USED FOR THIS PART OF THE EXAMINATION.

Directions: Solve each of the following problems, using the available space for scratchwork. After examining the form of the choices, decide which is the best of the choices given and fill in the corresponding oval on the answer sheet. No credit will be given for anything written in the test book. Do not spend too much time on any one problem.

In this test: Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers x for which f(x) is a real number.

1. The function f is given by f(x) = 3x⁴ — 2x³ + 7x — 2. On which of the following intervals is f' decreasing?

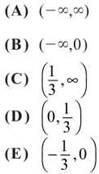
2. What is the area under the curve described by the parametric equations x = sint and y = cos²t for

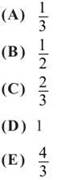
3. The function f is given by f(x) = 8x³+ 36x² + 54x + 27. All of these statements are true EXCEPT

(A) —3/2 is a zero of f.

(B) —3/2 is a point of inflection of f.

(D) —3/2 is a zero of the derivative of f

(E) f is strictly monotonic.

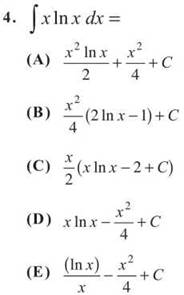
5. Let If g is decreasing for all x in its domain, then

(A) h is strictly increasing.

(B) h is strictly decreasing.

(D) both (B) and (C).

(E) none of the above.

QUESTIONS 6, 7, AND 8 REFER TO THE DIAGRAM AND INFORMATION BELOW.

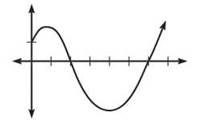
The function f is defined on [0,7]. The graph of its derivative, f', is shown above.

6. The point (2,5) is on the graph of y = f(x). An equation of the line tangent to the graph off at (2,5) is

(A) y = 2

(B) y = 5

(D) y = 2x + 5

(E) y = 2x — 5

7. How many points of inflection does the graph y = f(x) have over [0,7]?

(A) 0

(B) 1

(D) 3

(E) 4

8. At what value of x does the absolute maximum value of f occur?

(A) 1

(B) 2

(D) 6

(E) 7

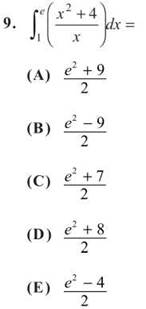
10. The function/ given by f(x) = 3x⁵ — 4x³ — 3x is increasing and concave up over which of these intervals?

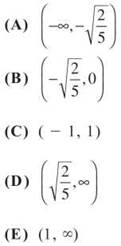
11. If y = 2xy — x² + 3, then when x = 1, dy/dx =

(A) -6

(B) -2

(D) 2

(E) 6

12. The length of the curve described by the parametric equations x = 2t³ and y = t³ where 0 ≤ t ≤ 1 is

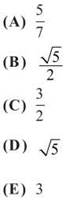
13. What is the average value of f(x) = 3sin²x — cos²x over [0,π/2]?

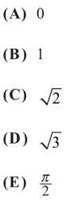
14. Let f be defined as 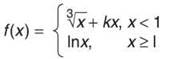for some constant k. For what value of k will f be differentiable over its whole domain?

(A) -2

(B) -1

(D) 1

(E) None of the above

15. What is the approximation of the value of e³ obtained by using a fourth-degree Taylor polynomial about x = 0 for e^x?

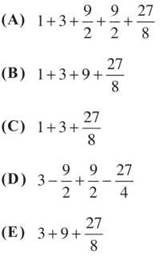
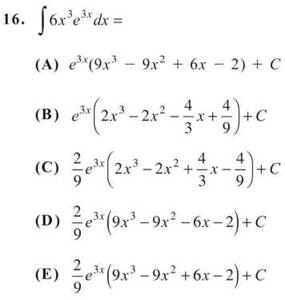
17. If f(x) = secx, then f'(x) has how many zeros over the closed interval [0,2π]?

(A) 0

(B) 1

(D) 3

(E) 4

18. Consider the region in the first quadrant bounded by y = x² over [0,3]. Let L₃ represent the Riemann approximation of the area of this region using left endpoints and three rectangles, R₃represent the Riemann approximation using right endpoints and three rectangles, M₃ represent the Riemann approximation using midpoints and three rectangles, and T₃ represent the trapezoidal approximation with three trapezoids. Which of the following statements is true?

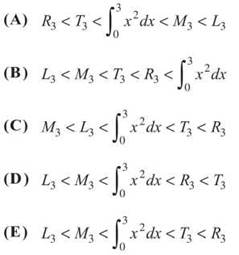
19. Which of the following series converge?

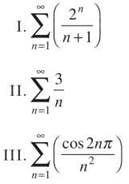
(A) I only

(B) II only

(D) I and II

(E) I and III

20. The area of the region inside the polar curve r = 4sinθ but outside the polar curve r = 2√2 is given by

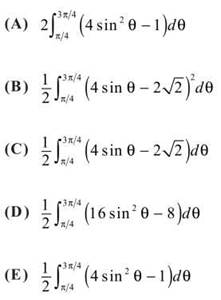
21. When x = 16, the rate at which x^3/4 is increasing is k times the rate at which √x is increasing. What is the value of k?

(A) 1/8

(B) 3/8

(D) 3

(E) 8

22. The length of the path described by the parametric equations x = 2cos2t and y = sin²t for 0 ≤ t ≤ π is given by

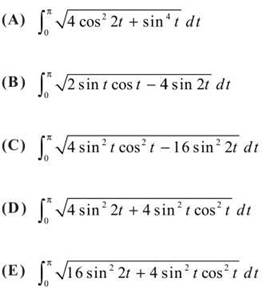
23. Determine the interval of convergence for the series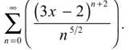

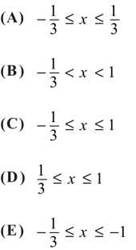
24. has a horizontal asymptote at x =

(A) 3/2

(B) 3/2 and -1/2

(D) -3/4 and 1/2

(E) None of the above

25.

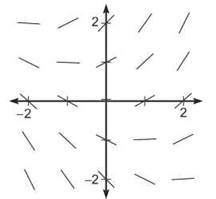
Shown above is the slope field for which of the following differential equations?

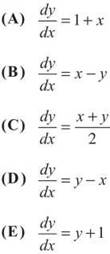
27. The population P(t) of a species satisfies the logistic differential equatlon What is

(A) 100

(B) 200

(D) 400

(E) 500

28. If is a Taylor series that converges to f(x) for every real x, then f"(c) =

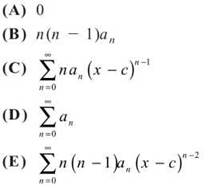
STOP. END OF SECTION I, FART A. IF YOU HAVE ANY TIME LEFT, GO OVER YOUR WORK IN THIS PART ONLY. DO NOT WORK IN ANY OTHER PART OF THE TEST.

SECTION I, PART B

50 Minutes • 17 Questions

A GRAPHING CALCULATOR IS REQUIRED FOR SOME QUESTIONS IN THIS PART OF THE EXAMINATION.

In this test: (1) The exact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among the choices the number that best approximates the exact numerical value. (2) Unless otherwise specified, the domain of a function/is assumed to be the set of all real numbers x for which f(x) is a real number.

29. The graph of the function represented by the Taylor series, centered at x = 1, 1 — (x — 1) + (x — 1)² — (x — 1)³ + ... = (—1)ⁿ(x — 1)ⁿ intersects the graph of y = e^x at x —

(A) -9.425

(B) 0.567

(D) 0.773

(E) 1.763

30. If f is a vector-valued function defined by f(t) = 2t, ln t>, then f’’(t) =

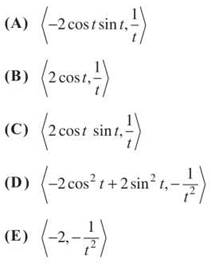
31. The diagonal of a square is increasing at a constant rate of √2 centimeters per second. In terms of the perimeter, P, what is the rate of change of the area of the square in square centimeters per second?

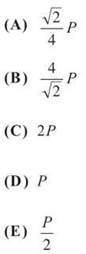
32. If f is continuous over the set of real numbers and f is defined as for all x ≠ 2, then f(2) =

(A) -2

(B) -1

(D) 1

(E) 2

33. If 0 ≤ k ≤ 2 and the area between the curves y = x² + 4 and y = x³ from x = 0 to x = k is 5, then k =

(A) 1.239

(B) 1.142

(D) 0.941

(E) 0.876

34. Determine dy/dx for the curve defined by xsiny = 1.

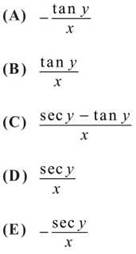
35. If f(x) = h(x) + g(x) for 0 ≤ x ≤ 10, then

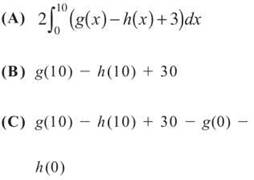
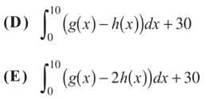
36. Use a fifth-degree Taylor polynomial centered at x = 0 to estimate e².

(A) 7.000

(B) 7.267

(D) 7.389

(E) 7.667

37. What are all the values of x for which the series 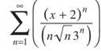converses?

38. Let Let R be the region bounded by f, the x-axis, and the vertical lines x = —3 and x = 3. Let T₆ represent the approximation of the area of R using the trapezoidal rule with n = 6. The quotient

(A) 0.334

(B) 0.978

(D) 1.304

(E) 4.666

39. Let R be the region bounded by y = 3 — x², y = x³ + 1, and x = 0. If R is rotated about the x-axis, the volume of the solid formed could be determined by

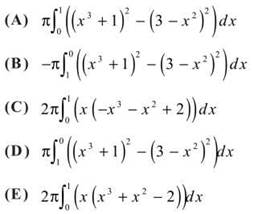
40. Let f be defined as 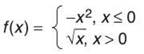and g be defined as for —4 ≤ t ≤ 4. Which of these is an equation for the tangent line to g at x = 2?

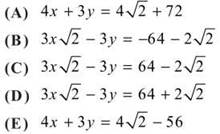
41.

Let where a ≤ x ≤ b. The figure above shows the graph of g on [a,b]. Which of the following could be the graph of f on [a,b].

42. The sum of the infinite geometric series is

(A) 0.622

(B) 0.893

(D) 1.429

(E) 2.800

43. Let f be a strictly monotonic differentiable function on the closed interval [5.10] such that f(5) = 6 and f(10) = 26. Which of the following must be true for the function/on the interval [5.10]?

I. The average rate of change of f is 4.

II. The absolute maximum value of f is 26.

III. f'(8) > 0.

(A) I only

(B) II only

(D) I and II

(E) I, II, and III

44. Let F(x) be an antiderivative of f(x) = e^2x. If F(0) = 2.5, then F(5) =

(A) 150.413

(B) 11013.233

(D) 22026.466

(E) 22028.466

45. The base of a solid is the region in the first quadrant bounded by y = —x² + 3. The cross sections perpendicular to the x-axis are squares. Find the volume of the solid.

(A) 3.464

(B) 8.314

(D) 16.628

(E) 21.600

STOP. END OF SECTION I, PART B. IF YOU HAVE ANY TIME LEFT, GO OVER YOUR WORK IN THIS PART ONLY. DO NOT WORK IN ANY OTHER PART OF THE TEST.

SECTION II, PART A

45 Minutes • 3 Questions

A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS IN THIS PART OF THE EXAMINATION.

SHOW ALL YOUR WORK. It is important to show your setups for these problems because partial credit will be awarded. If you use decimal approximations, they should be accurate to three decimal places.

1. Let f be a function that has derivatives of all orders for all real numbers. Assume f(1) = 3, f'(1) = -1, f"(1) = 4, and f"'(1) = -2.

(a) Write the third-degree Taylor polynomial for f about x = 1, and use it to approximate f(1.1).

(b) Write the second-degree Taylor polynomial for f' about x = 1, and use it to approximate f(1.1).

(d) Can f(2) be determined from the information given? Justify your answer.

2. Consider the differential equation

(a) Find a solution y = f(x) to the differential equation that satisfies f(0) = 2.

(b) What is the domain of f?

3. Let R be the region enclosed by the graphs of y = —x² + 3 and y = tan^-1x.

(a) Determine the area of R.

(b) Write an expression involving one or more integrals that gives the length of the boundary of R. Do not evaluate.

(c) The base of a solid is the region R. The cross sections perpendicular to the x-axis are semicircles. Write an expression involving one or more integrals that gives the volume of the solid. Do not evaluate.

STOP. END OF SECTION II, PART A. IF YOU HAVE ANY TIME LEFT, GO OVER YOUR WORK IN THIS PART ONLY. DO NOT WORK IN ANY OTHER FART OF THE TEST.

SECTION II, PART B

45 Minutes • 3 Questions

A CALCULATOR IS NOT PERMITTED FOR THIS PART OF THE EXAMINATION.

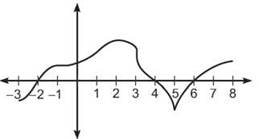
The figure above shows the graph of f', the derivative of some function f, for —3 ≤ x ≤ 8. The graph of f' has horizontal tangent lines at x = —1 and x = 2, a vertical tangent line at x = 3, and a cusp at x = 5.

(a) Find all values of x for which f attains a relative minimum on (—3,8). Explain.

(b) Find all values of x for which f attains a relative maximum on (—3,8). Explain.

(d) For what value(s) of x, for —3 < x < 8, does f"(x) not exist?

5. Consider the differential equation

(a) On the axes provided below, sketch a slope field for the given differential equation at the nine points indicated.

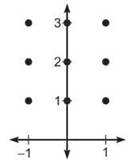
(b) Let y = f(x) be a particular solution to the given differential equation with the initial condition f(0) = 3. Use Euler’s method starting at x = 0 with a step size of 0.2 to approximate f(0.4). Show the work that leads to your answer.

6. A moving particle has position (x(t), y(t) at time t. The position of the particle at time t = 1 is (7,0), and the velocity vector at any time t > 0 is given by

(a) Find the position of the particle at t = 3.

(b) Will the line tangent to the path of the particle at (x(t), y(t) ever have a slope of zero? If so, when? If not, why not?

STOP. END OF SECTION II, PART B. IF YOU HAVE ANY TIME LEFT, GO OVER YOUR WORK IN THIS PART ONLY. DO NOT WORK IN ANY OTHER PART OF THE TEST.