Calculus AB and Calculus BC

CHAPTER 1 Functions

G. POLAR FUNCTIONS

Polar coordinates of the form (r, ) identify the location of a point by specifying , an angle of rotation from the positive x-axis, and r, a distance from the origin, as shown in Figure N1–14.

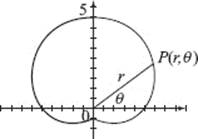
FIGURE N1–14

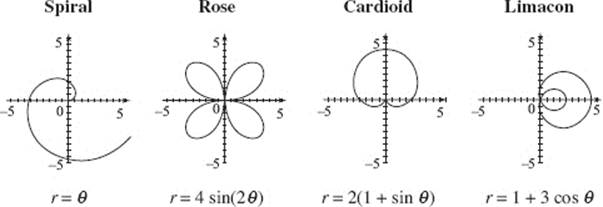
A polar function defines a curve with an equation of the form r = f (). Some common polar functions include:

EXAMPLE 17

Consider the polar function r = 2 + 4 sin .

(a) For what values of in the interval [0,2π] does the curve pass through the origin?

(b) For what value of in the interval [0,π/2] does the curve intersect the circle r = 3?

SOLUTION:

(a) At the origin r = 0, so we want 2 + 4 sin = 0. Solving for yields which occurs at

(b) The curves r = 2 + 4 sin and r = 3 intersect when 2 + 4 sin = 3, or From the calculator we find = arcsin

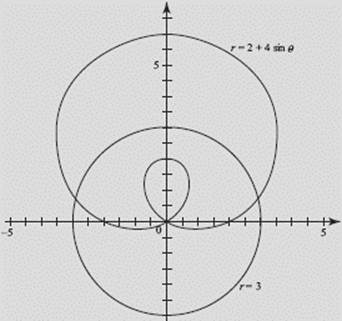
FIGURE N1–15

A polar function may also be expressed parametrically:

x = r cos , y = sin

In this form, the curve r = 2 + 4 sin from Example 17 would be defined by:

x() = (2 + 4 sin ) cos , y() = (2 + 4 sin ) sin

EXAMPLE 18

Find the (x, y) coordinates of the point on r = 1 + cos where

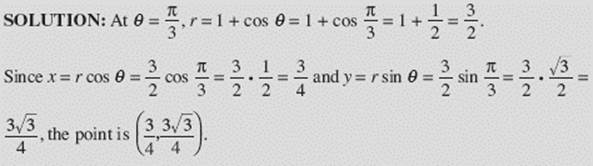
Chapter Summary

This chapter has reviewed some important precalculus topics. These topics are not directly tested on the AP exam; rather, they represent basic principles important in calculus. These include finding the domain, range and inverse of a function; and understanding the properties of polynomial and rational functions, trigonometric and inverse trig functions, and exponential and logarithmic functions.

For BC students, this chapter also reviewed parametrically defined functions.