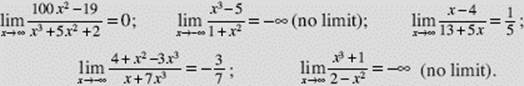Calculus AB and Calculus BC

CHAPTER 2 Limits and Continuity

D. LIMIT OF A QUOTIENT OF POLYNOMIALS

To find where P(x) and Q(x) are polynomials in x, we can divide both numerator and denominator by the highest power of x that occurs and use the fact that

EXAMPLE 18

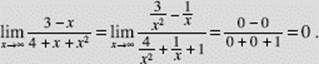
EXAMPLE 19

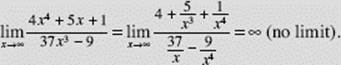
EXAMPLE 20

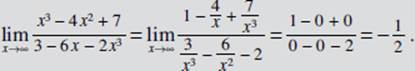
THE RATIONAL FUNCTION THEOREM

We see from Examples 18, 19, and 20 that: if the degree of P(x) is less than that of Q(x), then if the degree of P(x) is higher than that of Q(x), then (i.e., does not exist); and if the degrees of P(x) and Q(x) are the same, then where a_n and b_n are the coefficients of the highest powers of x in P(x) and Q(x), respectively.

This theorem holds also when we replace “x → ∞” by “x → −∞.” Note also that:

(i) when then y = 0 is a horizontal asymptote of the graph of

(ii) when then the graph of has no horizontal asymptotes;

(iii) when is a horizontal asymptote of the graph of

EXAMPLE 21