Calculus AB and Calculus BC

CHAPTER 2 Limits and Continuity

Practice Exercises

Part A. Directions: Answer these questions without using your calculator.

1.

(A) 1

(B) 0

(C)

(D) −1

(E) ∞

2.

(A) 1

(B) 0

(C) −4

(D) −1

(E) ∞

3.

(A) 0

(B) 1

(C)

(D) ∞

(E) none of these

4.

(A) 1

(B) 0

(C) ∞

(D) −1

(E) nonexistent

5.

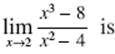
(A) 4

(B) 0

(C) 1

(D) 3

(E) ∞

6.

(A) −2

(B)

(C) 1

(D) 2

(E) nonexistent

7.

(A) −∞

(B) −1

(C) 0

(D) 3

(E) ∞

8.

(A) 3

(B) ∞

(C) 1

(D) −1

(E) 0

9.

(A) −1

(B) 1

(C) 0

(D) ∞

(E) none of these

10.

(A) −1

(B) 1

(C) 0

(D) ∞

(E) none of these

11.

(A) = 0

(B)

(C) = 1

(D) = 5

(E) does not exist

12.

(A) = 0

(B)

(C) = 1

(D)

(E) does not exist

13. The graph of y = arctan x has

(A) vertical asymptotes at x = 0 and x = π

(B) horizontal asymptotes at

(C) horizontal asymptotes at y = 0 and y = π

(D) vertical asymptotes at

(E) none of these

14. The graph of 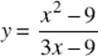has

(A) a vertical asymptote at x = 3

(B) a horizontal asymptote at

(C) a removable discontinuity at x = 3

(D) an infinite discontinuity at x = 3

(E) none of these

15.

(A) 1

(B)

(C) 3

(D) ∞

(E)

16.

(A) ∞

(B) 1

(C) nonexistent

(D) −1

(E) none of these

17. Which statement is true about the curve

(A) The line is a vertical asymptote.

(B) The line x = 1 is a vertical asymptote.

(C) The line is a horizontal asymptote.

(D) The graph has no vertical or horizontal asymptote.

(E) The line y = 2 is a horizontal asymptote.

18.

(A) −4

(B) −2

(C) 1

(D) 2

(E) nonexistent

19.

(A) 0

(B) nonexistent

(C) 1

(D) −1

(E) none of these

20.

(A) 0

(B) ∞

(C) nonexistent

(D) −1

(E) 1

21.

(A) 1

(B) 0

(C) ∞

(D) nonexistent

(E) none of these

22. Let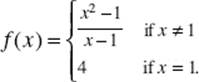

Which of the following statements is (are) true?

I. exists

II. f (1) exists

III. f is continuous at x = 1

(A) I only

(B) II only

(C) I and II

(D) none of them

(E) all of them

23.

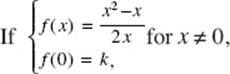
and if f is continuous at x = 0, then k =

(A) −1

(B)

(C) 0

(D)

(E) 1

24.

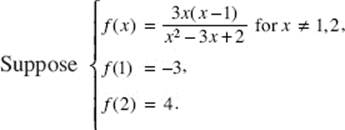
Then f (x) is continuous

(A) except at x = 1

(B) except at x = 2

(C) except at x = 1 or 2

(D) except at x = 0, 1, or 2

(E) at each real number

25. The graph of has

(A) one vertical asymptote, at x = 1

(B) the y-axis as vertical asymptote

(C) the x-axis as horizontal asymptote and x = ±1 as vertical asymptotes

(D) two vertical asymptotes, at x = ±1, but no horizontal asymptote

(E) no asymptote

26. The graph of has

(A) a horizontal asymptote at but no vertical asymptote

(B) no horizontal asymptote but two vertical asymptotes, at x = 0 and x = 1

(C) a horizontal asymptote at and two vertical asymptotes, at x = 0 and x = 1

(D) a horizontal asymptote at x = 2 but no vertical asymptote

(E) a horizontal asymptote at and two vertical asymptotes, at x = ±1

27.

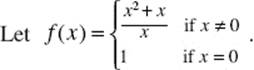
Which of the following statements is (are) true?

I. f (0) exists

II. exists

III. f is continuous at x = 0

(A) I only

(B) II only

(C) I and II only

(D) all of them

(E) none of them

Part B. Directions: Some of the following questions require the use of a graphing calculator.

28. If [x] is the greatest integer not greater than x, then is

(A)

(B) 1

(C) nonexistent

(D) 0

(E) none of these

29. (With the same notation) is

(A) −3

(B) −2

(C) −1

(D) 0

(E) none of these

30.

(A) is −1

(B) is infinity

(C) oscillates between −1 and 1

(D) is zero

(E) does not exist

31. The function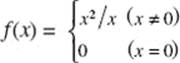

(A) is continuous everywhere

(B) is continuous except at x = 0

(C) has a removable discontinuity at x = 0

(D) has an infinite discontinuity at x = 0

(E) has x = 0 as a vertical asymptote

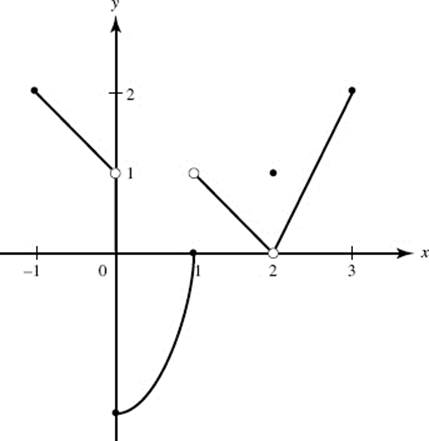
Questions 32–36 are based on the function f shown in the graph and defined below:

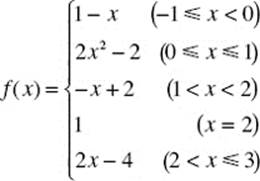
32.

(A) equals 0

(B) equals 1

(C) equals 2

(D) does not exist

(E) none of these

33. The function f is defined on [−1,3]

(A) if x ≠ 0

(B) if x ≠ 1

(C) if x ≠ 2

(D) if x ≠ 3

(E) at each x in [−1,3]

34. The function f has a removable discontinuity at

(A) x = 0

(B) x = 1

(C) x = 2

(D) x = 3

(E) none of these

35. On which of the following intervals is f continuous?

(A) −1 ≤ x ≤ 0

(B) 0 < x < 1

(C) 1 ≤ x ≤ 2

(D) 2 ≤ x ≤ 3

(E) none of these

36. The function f has a jump discontinuity at

(A) x = −1

(B) x = 1

(C) x = 2

(D) x = 3

(E) none of these

37.

(A) −∞

(B)

(C)

(D) ∞

(E) none of these

38. Suppose and f (−3) is not defined. Which of the following statements is (are) true?

I.

II. f is continuous everywhere except at x = −3.

III. f has a removable discontinuity at x = −3.

(A) None of them

(B) I only

(C) III only

(D) I and III only

(E) All of them

39. If 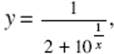then y is

(A) 0

(B)

(C)

(D)

(E) nonexistent

Questions 40–42 are based on the function f shown in the graph.

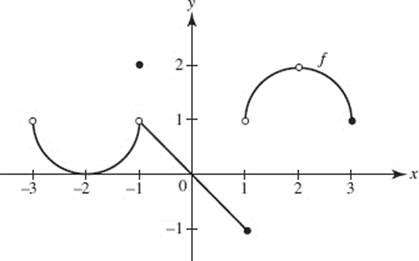
40. For what value(s) of a is it true that exists and f (a) exists, but It is possible that a =

(A) −1 only

(B) 1 only

(C) 2 only

(D) −1 or 1 only

(E) −1 or 2 only

41. does not exist for a =

(A) −1 only

(B) 1 only

(C) 2 only

(D) 1 and 2 only

(E) −1, 1, and 2

42. Which statements about limits at x = 1 are true?

I. exists.

II. exists.

III. exists.

(A) none of I, II, or III

(B) I only

(C) II only

(D) I and II only

(E) I, II, and III

Practice Exercises

Part A. Directions: Answer these questions without using your calculator.

1.

(A) 1

(B) 0

(C)

(D) −1

(E) ∞

2.

(A) 1

(B) 0

(C) −4

(D) −1

(E) ∞

3.

(A) 0

(B) 1

(C)

(D) ∞

(E) none of these

4.

(A) 1

(B) 0

(C) ∞

(D) −1

(E) nonexistent

5.

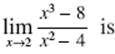
(A) 4

(B) 0

(C) 1

(D) 3

(E) ∞

6.

(A) −2

(B)

(C) 1

(D) 2

(E) nonexistent

7.

(A) −∞

(B) −1

(C) 0

(D) 3

(E) ∞

8.

(A) 3

(B) ∞

(C) 1

(D) −1

(E) 0

9.

(A) −1

(B) 1

(C) 0

(D) ∞

(E) none of these

10.

(A) −1

(B) 1

(C) 0

(D) ∞

(E) none of these

11.

(A) = 0

(B)

(C) = 1

(D) = 5

(E) does not exist

12.

(A) = 0

(B)

(C) = 1

(D)

(E) does not exist

13. The graph of y = arctan x has

(A) vertical asymptotes at x = 0 and x = π

(B) horizontal asymptotes at

(C) horizontal asymptotes at y = 0 and y = π

(D) vertical asymptotes at

(E) none of these

14. The graph of 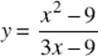has

(A) a vertical asymptote at x = 3

(B) a horizontal asymptote at

(C) a removable discontinuity at x = 3

(D) an infinite discontinuity at x = 3

(E) none of these

15.

(A) 1

(B)

(C) 3

(D) ∞

(E)

16.

(A) ∞

(B) 1

(C) nonexistent

(D) −1

(E) none of these

17. Which statement is true about the curve

(A) The line is a vertical asymptote.

(B) The line x = 1 is a vertical asymptote.

(C) The line is a horizontal asymptote.

(D) The graph has no vertical or horizontal asymptote.

(E) The line y = 2 is a horizontal asymptote.

18.

(A) −4

(B) −2

(C) 1

(D) 2

(E) nonexistent

19.

(A) 0

(B) nonexistent

(C) 1

(D) −1

(E) none of these

20.

(A) 0

(B) ∞

(C) nonexistent

(D) −1

(E) 1

21.

(A) 1

(B) 0

(C) ∞

(D) nonexistent

(E) none of these

22. Let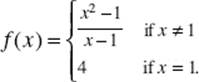

Which of the following statements is (are) true?

I. exists

II. f (1) exists

III. f is continuous at x = 1

(A) I only

(B) II only

(C) I and II

(D) none of them

(E) all of them

23.

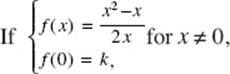
and if f is continuous at x = 0, then k =

(A) −1

(B)

(C) 0

(D)

(E) 1

24.

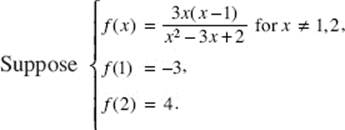
Then f (x) is continuous

(A) except at x = 1

(B) except at x = 2

(C) except at x = 1 or 2

(D) except at x = 0, 1, or 2

(E) at each real number

25. The graph of has

(A) one vertical asymptote, at x = 1

(B) the y-axis as vertical asymptote

(C) the x-axis as horizontal asymptote and x = ±1 as vertical asymptotes

(D) two vertical asymptotes, at x = ±1, but no horizontal asymptote

(E) no asymptote

26. The graph of has

(A) a horizontal asymptote at but no vertical asymptote

(B) no horizontal asymptote but two vertical asymptotes, at x = 0 and x = 1

(C) a horizontal asymptote at and two vertical asymptotes, at x = 0 and x = 1

(D) a horizontal asymptote at x = 2 but no vertical asymptote

(E) a horizontal asymptote at and two vertical asymptotes, at x = ±1

27.

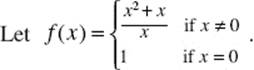
Which of the following statements is (are) true?

I. f (0) exists

II. exists

III. f is continuous at x = 0

(A) I only

(B) II only

(C) I and II only

(D) all of them

(E) none of them

Part B. Directions: Some of the following questions require the use of a graphing calculator.

28. If [x] is the greatest integer not greater than x, then is

(A)

(B) 1

(C) nonexistent

(D) 0

(E) none of these

29. (With the same notation) is

(A) −3

(B) −2

(C) −1

(D) 0

(E) none of these

30.

(A) is −1

(B) is infinity

(C) oscillates between −1 and 1

(D) is zero

(E) does not exist

31. The function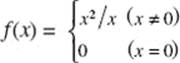

(A) is continuous everywhere

(B) is continuous except at x = 0

(C) has a removable discontinuity at x = 0

(D) has an infinite discontinuity at x = 0

(E) has x = 0 as a vertical asymptote

Questions 32–36 are based on the function f shown in the graph and defined below:

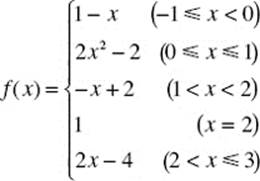
32.

(A) equals 0

(B) equals 1

(C) equals 2

(D) does not exist

(E) none of these

33. The function f is defined on [−1,3]

(A) if x ≠ 0

(B) if x ≠ 1

(C) if x ≠ 2

(D) if x ≠ 3

(E) at each x in [−1,3]

34. The function f has a removable discontinuity at

(A) x = 0

(B) x = 1

(C) x = 2

(D) x = 3

(E) none of these

35. On which of the following intervals is f continuous?

(A) −1 ≤ x ≤ 0

(B) 0 < x < 1

(C) 1 ≤ x ≤ 2

(D) 2 ≤ x ≤ 3

(E) none of these

36. The function f has a jump discontinuity at

(A) x = −1

(B) x = 1

(C) x = 2

(D) x = 3

(E) none of these

37.

(A) −∞

(B)

(C)

(D) ∞

(E) none of these

38. Suppose and f (−3) is not defined. Which of the following statements is (are) true?

I.

II. f is continuous everywhere except at x = −3.

III. f has a removable discontinuity at x = −3.

(A) None of them

(B) I only

(C) III only

(D) I and III only

(E) All of them

39. If 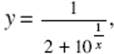then y is

(A) 0

(B)

(C)

(D)

(E) nonexistent

Questions 40–42 are based on the function f shown in the graph.

40. For what value(s) of a is it true that exists and f (a) exists, but It is possible that a =

(A) −1 only

(B) 1 only

(C) 2 only

(D) −1 or 1 only

(E) −1 or 2 only

41. does not exist for a =

(A) −1 only

(B) 1 only

(C) 2 only

(D) 1 and 2 only

(E) −1, 1, and 2

42. Which statements about limits at x = 1 are true?

I. exists.

II. exists.

III. exists.

(A) none of I, II, or III

(B) I only

(C) II only

(D) I and II only

(E) I, II, and III