Calculus AB and Calculus BC

CHAPTER 3 Differentiation

G. IMPLICIT DIFFERENTIATION

When a functional relationship between x and y is defined by an equation of the form F(x, y) = 0, we say that the equation defines y implicitly as a function of x. Some examples are x² + y² − 9 = 0, y² − 4x = 0, and cos (xy) = y² − 5 (which can be written as cos (xy) − y² + 5 = 0). Sometimes two (or more) explicit functions are defined by F(x, y) = 0. For example, x² + y² − 9 = 0 defines the two functions the upper and lower halves, respectively, of the circle centered at the origin with radius 3. Each function is differentiable except at the points where x = 3 and x = −3.

Implicit differentiation is the technique we use to find a derivative when y is not defined explicitly in terms of x but is differentiable.

In the following examples, we differentiate both sides with respect to x, using appropriate formulas, and then solve for

EXAMPLE 27

If x² + y² − 9 = 0, then

Note that the derivative above holds for every point on the circle, and exists for all y different from 0 (where the tangents to the circle are vertical).

EXAMPLE 28

If x² − 2xy + 3y² = 2, find

SOLUTION: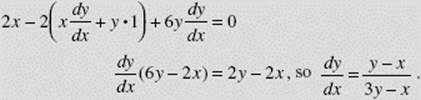

EXAMPLE 29

If x sin y = cos (x + y), find

SOLUTION: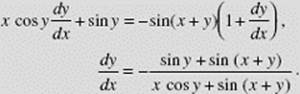

EXAMPLE 30

Find using implicit differentiation on the equation x² + y² = 1.

SOLUTION:

Then

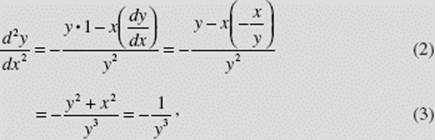
where we substituted for from (1) in (2), then used the given equation to simplify in (3).

EXAMPLE 31

Using implicit differentiation, verify the formula for the derivative of the inverse sine function, y = sin⁻¹ x = arcsin x, with domain [−1,1] and range

SOLUTION: y = sin⁻¹ x ↔ x = sin y.

Now we differentiate with respect to x:

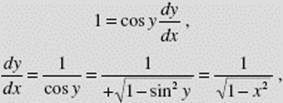
where we chose the positive sign for cos y since cos y is nonnegative if Note that this derivative exists only if −1 < x < 1.