Calculus AB and Calculus BC

CHAPTER 4 Applications of Differential Calculus

D. MAXIMUM, MINIMUM, AND INFLECTION POINTS: DEFINITIONS

The curve of y = f (x) has a local (or relative) at a point where x = c if for all x in the immediate neighborhood of c. If a curve has a local at x = c, then the curve changes from as x increases through c. If a function is differentiable on the closed interval [a, b] and has a local maximum or minimum at x = c (a < c < b), then f ′(c) = 0. The converse of this statement is not true.

If f (c) is either a local maximum or a local minimum, then f (c) is called a local extreme value or local extremum. (The plural of extremum is extrema.)

The global or absolute of a function on [a, b] occurs at x = c if for all x on [a, b].

A curve is said to be concave at a point P(x₁, y₁) if the curve lies its tangent. If at P, the curve is concave In Figure N4–1, the curves sketched in (a) and (b) are concave downward at P while in (c) and (d) they are concave upward at P.

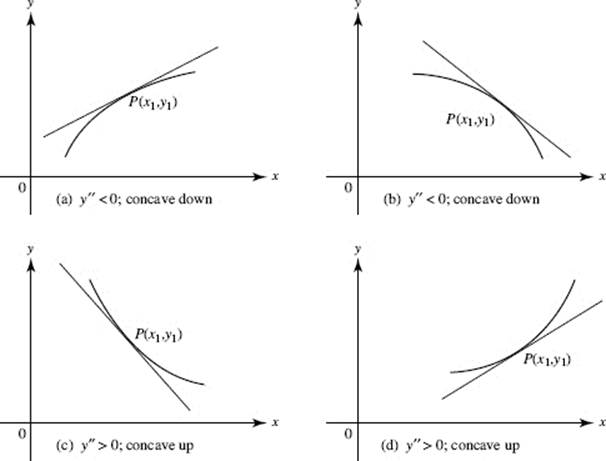
FIGURE N4–1

Point of inflection

A point of inflection is a point where the curve changes its concavity from upward to downward or from downward to upward. See §I, for a table relating a function and its derivatives. It tells how to graph the derivatives of f, given the graph of f.