Calculus AB and Calculus BC

CHAPTER 4 Applications of Differential Calculus

H. OPTIMIZATION: PROBLEMS INVOLVING MAXIMA AND MINIMA

The techniques described above can be applied to problems in which a function is to be maximized (or minimized). Often it helps to draw a figure. If y, the quantity to be maximized (or minimized), can be expressed explicitly in terms of x, then the procedure outlined above can be used. If the domain of y is restricted to some closed interval, one should always check the endpoints of this interval so as not to overlook possible extrema. Often, implicit differentiation, sometimes of two or more equations, is indicated.

EXAMPLE 21

The region in the first quadrant bounded by the curves of y² = x and y = x is rotated about the y-axis to form a solid. Find the area of the largest cross section of this solid that is perpendicular to the y-axis.

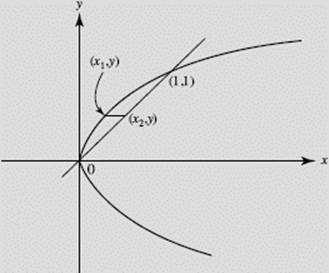
FIGURE N4–9

SOLUTION: See Figure N4–9. The curves intersect at the origin and at (1,1), so 0 < y < 1. A cross section of the solid is a ring whose area A is the difference between the areas of two circles, one with radius x₂, the other with radius x₁. Thus

The only relevant zero of the first derivative is There the area A is

Note that = π(2 − 12y²) and that this is negative when assuring a maximum there. Note further that A equals zero at each endpoint of the interval [0,1] so that is the global maximum area.

EXAMPLE 22

The volume of a cylinder equals V cubic inches, where V is a constant. Find the proportions of the cylinder that minimize the total surface area.

FIGURE N4–10

SOLUTION: We know that the volume is

where r is the radius and h the height. We seek to minimize S, the total surface area, where

Solving (1) for h, we have which we substitute in (2):

Differentiating (3) with respect to r yields

Now we set equal to zero to determine the conditions that make S a minimum:

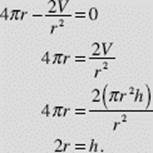
The total surface area of a cylinder of fixed volume is thus a minimum when its height equals its diameter.

(Note that we need not concern ourselves with the possibility that the value of r that renders equal to zero will produce a maximum surface area rather than a minimum one. With V fixed, we can choose r and h so as to make S as large as we like.)

EXAMPLE 23

A charter bus company advertises a trip for a group as follows: At least 20 people must sign up. The cost when 20 participate is $80 per person. The price will drop by $2 per ticket for each member of the traveling group in excess of 20. If the bus can accommodate 28 people, how many participants will maximize the company’s revenue?

SOLUTION: Let x denote the number who sign up in excess of 20. Then 0 x 8. The total number who agree to participate is (20 + x), and the price per ticket is (80 − 2x) dollars. Then the revenue R, in dollars, is

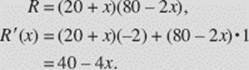
R ′(x) is zero if x = 10. Although x = 10 yields maximum R—note that R ″(x) = −4 and is always negative—this value of x is not within the restricted interval. We therefore evaluate R at the endpoints 0 and 8: R(0) = 1600 and R(8) = 28·64 = 1792, 28 participants will maximize revenue.

EXAMPLE 24

A utilities company wants to deliver gas from a source S to a plant P located across a straight river 3 miles wide, then downstream 5 miles, as shown in Figure N4–11. It costs $4 per foot to lay the pipe in the river but only $2 per foot to lay it on land.

(a) Express the cost of laying the pipe in terms of u.

(b) How can the pipe be laid most economically?

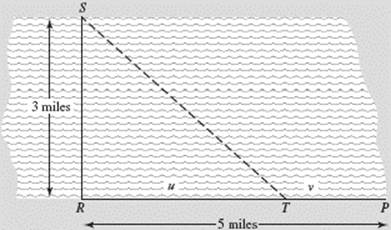
FIGURE N4–11

SOLUTIONS:

(a) Note that the problem “allows” us to (1) lay all of the pipe in the river, along a line from S to P; (2) lay pipe along SR, in the river, then along RP on land; or (3) lay some pipe in the river, say, along ST, and lay the rest on land along TP. When T coincides with P, we have case (1), with v = 0; when T coincides with R, we have case (2), with u = 0. Case (3) includes both (1) and (2).

In any event, we need to find the lengths of pipe needed (that is, the distances involved); then we must figure out the cost.

In terms of u:

If C(u) is the total cost,

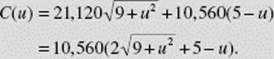
(b) We now minimize C(u):

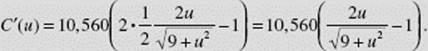
We now set C ′(u) equal to zero and solve for u:

where, in the last step, we squared both sides; then

4u² = 9 + u², 3u² = 9, u² = 3, u =

where we discard u = − as meaningless for this problem.

The domain of C(u) is [0,5] and C is continuous on [0,5], Since

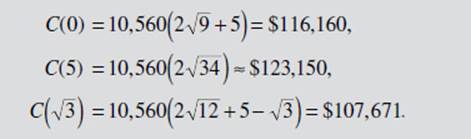
So u = yields minimum cost. Thus, the pipe can be laid most economically if some of it is laid in the river from the source S to a point T that is miles toward the plant P from R, and the rest is laid along the road from T to P.